Average Treatment Effect
Average Treatment Effect
Example
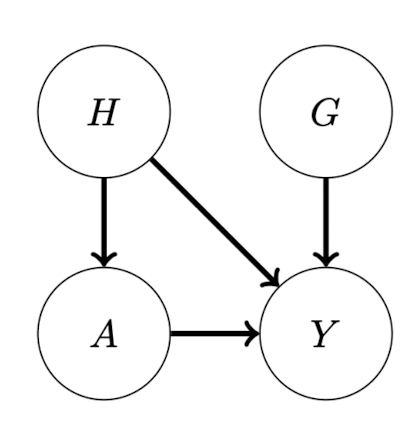
먼저, 이번 글에서 다룰 Structural Causal Model로 다음과 같은 예제를 설정하자. 아래 SCM은 흡연 여부 $A$, 암 발병여부 $Y$, 건강 자각도(?)health conciousness $H$, 그리고 유전적 요인 $G$의 인과관계에 대한 것이다. 이때 처치변수는 노드 $A$에 해당한다.
Definition
SCM에서 처치(Treatment)의 효과를 파악하기 위해서는, 먼저 처치효과의 크기를 어떻게 정의할 것인가에 대한 고민이 선행되어야 한다. 가장 직관적으로 처치변수가 $A$라고 할 때, $A=1$(처치 O)인 경우와 $A=0$(처치 X)인 경우의 결과를 비교하면 될 것이다. 이러한 방법으로 측정하는 처치효과를 평균처치효과, Average Treatment Effect라고 하며 줄여서 ATE라고도 부른다. 이는 다음과 같이 정의된다.
\[\mathrm{ATE} = \mathrm{E}[Y\vert do(A=1)]-\mathrm{E}[Y \vert do(A=0)]\tag{1}\]즉, 처치변수에 대한 두 intervention에 대해 평균 output의 차이로 정의된다.
Identification
ATE의 정의에서, 각 intervention에 대한 average output $\mathrm{E}[Y\vert do(A=1)]$ 을 causal estimand라고 부른다.
Causal estimands : 잠재적 결과변수 $Y$ 의 함수
그러나, 현실에서는 관측한 표본으로부터 인과구조를 곧바로 파악하는 것이 매우 어렵기 때문에, intervention에 대한 확률분포 $P(Y\vert do(A=1))$ 을 학습할 수 없다. 따라서, 근본적으로 인과구조에 대한 가정들이 필요하다. 이때, 만일 어떤 가정들 하에서 해당 causal estimand가 유일한 값으로 추정되는 경우 이를 식별가능identifiable하다고 정의한다.
또한, 만일 causal estimand가 해당 가정들 하에서 관측가능한 확률분포들의 함수로 표현가능하다면 이를 statistical estimand라고 정의한다. 위 example에서 ATE(식 1)은 다음과 같은 statistical estimand와 동일하다.
\[\mathrm{ATE} \overset{(*)}{=} \tau^{\mathrm{ATE}} := \mathrm{E}[\mathrm{E}[Y\vert H,A=1]-\mathrm{E}[Y\vert H,A=0]]\]여기서 등식 $(*)$이 성립하는 이유는 SCM의 성질 때문이며, 우변의 경우 관측가능한 변수들로만 구성된 조건부 기댓값이기 때문에 $\tau$는 관측가능한 확률분포의 함수, 즉 statistical estimand이다. Statistical estimand는 SCM에 대한 일종의 모수parameter라고 생각하면 된다.
또한, 식별가능한 causal estimand를 위해, 위 예시에 대해서는 다음과 같은 가정 집합을 생각할 수 있다.
- 암이 발병할 확률은 $A,G,H$에 대한 로지스틱 회귀모형으로 구성할 수 있다.
- 임의의 개인에 대해 흡연은 암의 발병확률에 non-negative한 영향을 가진다.
- 흡연 여부는 건강자각도의 영향을 받지만, 유전적 특성으로부터는 영향을 받지 않는다.
이러한 가정 집합으로부터 위 예시와 같은 SCM을 식별해낼 수 있다.
References
- K. Murphy, Probabilistic Machine Learning - Advanced Topics.
Leave a comment