Bayesian Network and Markov Random Field
본 포스트는 서울대학교 M2480.001200 인공지능을 위한 이론과 모델링 강의노트를 간단히 재구성한 것입니다.
Bayesian Network
Bayesian network는 아래 예시와 같은 방향성 비순환 그래프(Directed Acyclic graph)를 의미합니다.
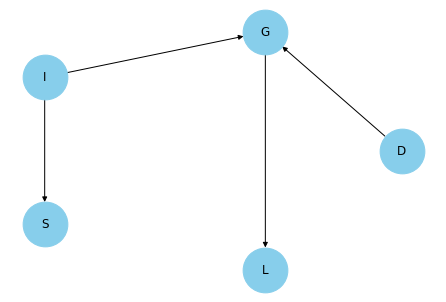
각 노드는 확률변수에 대응되는데, (위 예시는 PGM의 유명한 예제인 student network입니다) 각각의 확률변수는 다음의 의미를 나타냅니다.
- D : difficulty of course (과목 난이도)
- I : intelligence (개인의 지능 e.g. IQ)
- S : SAT score (SAT 점수)
- G : grade (과목 성적)
- L : letter(A,B,C,D…) (과목 표시 등급)
BN의 경우 각 확률변수의 조건부 분포(CPD)를 모델링할 수 있는데, 위 예시의 경우 아래와 같습니다.
CPD of D:
+------+-----+
| D(0) | 0.6 |
+------+-----+
| D(1) | 0.4 |
+------+-----+
CPD of I:
+------+-----+
| I(0) | 0.7 |
+------+-----+
| I(1) | 0.3 |
+------+-----+
CPD of S:
+------+------+------+
| I | I(0) | I(1) |
+------+------+------+
| S(0) | 0.95 | 0.2 |
+------+------+------+
| S(1) | 0.05 | 0.8 |
+------+------+------+
CPD of G:
+------+------+------+------+------+
| I | I(0) | I(0) | I(1) | I(1) |
+------+------+------+------+------+
| D | D(0) | D(1) | D(0) | D(1) |
+------+------+------+------+------+
| G(0) | 0.3 | 0.05 | 0.9 | 0.5 |
+------+------+------+------+------+
| G(1) | 0.4 | 0.25 | 0.08 | 0.3 |
+------+------+------+------+------+
| G(2) | 0.3 | 0.7 | 0.02 | 0.2 |
+------+------+------+------+------+
CPD of L:
+------+------+------+------+
| G | G(0) | G(1) | G(2) |
+------+------+------+------+
| L(0) | 0.1 | 0.4 | 0.99 |
+------+------+------+------+
| L(1) | 0.9 | 0.6 | 0.01 |
+------+------+------+------+
Properties of BN
BN에서는 전체 확률변수들의 결합확률밀도함수(혹은 결합확률질량함수) joint pdf가 다음과 같이 local conditional distribution들의 곱으로 나타납니다. 이를 Global Markov Independence라고 합니다.
\[P(X_{1},\ldots,X_{n}) = \prod_{i=1,\ldots,n}P(X_{i}\vert \mathrm{PA}_{X_{i}})\]여기서 $PA_{X_{i}}$는 $i$번째 노드의 부모 노드(parent node)의 집합을 의미합니다. 즉, 위 예시의 경우 다음과 같이 결합확률분포를 표현할 수 있게 됩니다.
\[P(D,I,S,G,L) = P(D)\cdot P(I)\cdot P(S\vert I)\cdot P(G\vert D,I)\cdot P(L\vert G)\]이러한 표현의 장점은, 모수공간의 차원 축소가 가능하다는 것입니다. 즉, 5개의 변수가 모두 이진형 변수(binary)라고 가정하면 결합확률분포를 표현하기 위해서는 $2^5-1=31$ 개의 모수가 필요합니다. 그러나 BN의 성질을 이용하면, 위 예시의 경우 $1+1+4+12+6=24$ 개의 모수만을 요구합니다. 24개의 모수만으로, 모든 경우에 대한 조건부 확률을 계산할 수 있게 됩니다.
예를 들어, $I=1, D=0$인 경우 $L$의 조건부 확률분포는 다음과 같이 계산됩니다.
import itertools
from pgmpy.inference.base import Inference
from pgmpy.factors import factor_product
class SimpleInference(Inference):
def __init__(self, model):
super().__init__(model)
self.factors = {node: [] for node in self.model.nodes()}
for cpd in self.model.get_cpds():
factor = cpd.to_factor()
for var in factor.scope():
self.factors[var].append(factor)
def query(self, var, evidence):
# self.factors is a dict of the form of {node: [factors_involving_node]}
factors_list = set(itertools.chain(*self.factors.values()))
product = factor_product(*factors_list)
reduced_prod = product.reduce(evidence, inplace=False)
reduced_prod.normalize()
var_to_marg = set(self.model.nodes()) - set(var) - set([state[0] for state in evidence])
marg_prod = reduced_prod.marginalize(var_to_marg, inplace=False)
return marg_prod
infer = SimpleInference(student_model)
l1 = infer.query(var=['L'], evidence=[('I', 1), ('D', 0)])
print(l1)
# Result
+------+----------+
| L | phi(L) |
+======+==========+
| L(0) | 0.1418 |
+------+----------+
| L(1) | 0.8582 |
+------+----------+
Local Semantics
각 노드 $X$에 대해 parent, ancestor, descendant 노드 집합은 다음과 같이 정의됩니다.
- Parent : $X$로 직접 향하는 변(화살표)이 있는 노드
- Ancestor : $X$로 향하는 경로(path)가 존재하는 노드
- Child : $X$에서 직접 향하는 변이 있는 노드
- Descendant : $X$로부터의 경로가 존재하는 노드
이때, BN에서는 다음이 성립합니다.
\[X \perp \mathrm{NonDesc}(X) \vert \mathrm{Pa}(X)\]Markov Blanket
각 노드 $X$에 대한 Markov blanket은 다음과 같이 정의됩니다.
\[MB_{X} = \mathrm{Pa}(X) \cup \mathrm{Child}(X) \cup \mathrm{Pa}(\mathrm{Child}(X))\]정의로부터 다음이 성립하는데, 이를 Local Markov Independence라고 합니다.
\[X \perp (V-X-MB_{X})\vert MB_{X}\]또한, Global MI와 Local MI는 동치임이 정리로 알려져 있습니다.
I-Maps
임의의 결합확률분포 $P$에 대해, 그래프 $G$가 $P$의 I-map이라는 것은 $G$에 존재하는 모든 Markov Independence(MI)가 $P$에 내포된 것을 의미합니다. 또한, 그래프 혹은 확률분포의 모든 독립성을 나타내는 집합을 $I(G), I(P)$ 와 같이 표기합니다. I-Map은 $I(G)\subset I(P)$ 인 경우를 의미합니다.
앞선 예시에서 $I(G)$ 는 다음과 같습니다.
# I-map
imap = student_model.get_independencies()
for i,v in enumerate(imap.get_assertions()):
# print five assertions per line
if i % 5 == 0:
print()
print(v, end=', ')
# Result
(L ⟂ S | I), (L ⟂ D, I, S | G), (L ⟂ S | I, D), (L ⟂ I, S | D, G), (L ⟂ D, S | I, G),
(L ⟂ I, D | S, G), (L ⟂ S | I, D, G), (L ⟂ I | S, D, G), (L ⟂ D | I, S, G), (I ⟂ D),
(I ⟂ D | S), (I ⟂ L | G), (I ⟂ L | D, G), (I ⟂ L | S, G), (I ⟂ L | S, D, G),
(S ⟂ D), (S ⟂ L, D, G | I), (S ⟂ L | G), (S ⟂ D, G | L, I), (S ⟂ L, G | I, D),
(S ⟂ L, D | I, G), (S ⟂ L | D, G), (S ⟂ G | L, I, D), (S ⟂ D | L, I, G), (S ⟂ L | I, D, G),
(G ⟂ S | I), (G ⟂ S | I, D), (G ⟂ S | L, I), (G ⟂ S | L, I, D), (D ⟂ I, S),
(D ⟂ S | I), (D ⟂ I | S), (D ⟂ L | G), (D ⟂ S | L, I), (D ⟂ L, S | I, G),
(D ⟂ L | S, G), (D ⟂ S | L, I, G), (D ⟂ L | I, S, G),
주목할 것은, I-Map은 유일하지 않으며 만일 모든 노드가 연결되어 있는 Full Bayesian Network $F$를 생각하면 이 역시도 I-Map이 된다는 것입니다 ($I(F) = \phi$ 이므로).
D-separation
BN에서 노드 $X,Y$가 $Z$가 주어질 때 d-separated 된다는 의미는 $Z$의 조건 하에서(조건부) 노드 $X$와 $Y$ 사이의 active path가 존재하지 않는다는 것을 의미합니다. 즉, 조건부 독립 $X\perp Y\vert Z$ 을 의미합니다. BN에서 특히 주의할 것은, v-structure $X\rightarrow Z \leftarrow Y$ 는 $Z$가 관측되면 active하고, 그렇지 않은 경우 blocked된다는 것입니다.
위 예시에서 $D,G,I$ 노드는 v-structure를 형성하고 있습니다. 실제로 확률을 계산해보면, $I,D$의 결합분포가 $G$의 조건 여부에 따라 달라집니다.
l2 = infer.query(var=['I'], evidence=[('G', 1), ('D', 0)])
print(l2)
l3 = infer.query(var=['I'], evidence=[('G', 1)])
print(l3)
l4 = infer.query(var=['I'], evidence=[('D', 0)])
print(l4)
l5 = infer.query(var=['I'], evidence=[])
print(l5)
#l2
+------+----------+
| I | phi(I) |
+======+==========+
| I(0) | 0.9211 |
+------+----------+
| I(1) | 0.0789 |
+------+----------+
#l3
+------+----------+
| I | phi(I) |
+======+==========+
| I(0) | 0.8252 |
+------+----------+
| I(1) | 0.1748 |
+------+----------+
#l4
+------+----------+
| I | phi(I) |
+======+==========+
| I(0) | 0.7000 |
+------+----------+
| I(1) | 0.3000 |
+------+----------+
#l5
+------+----------+
| I | phi(I) |
+======+==========+
| I(0) | 0.7000 |
+------+----------+
| I(1) | 0.3000 |
+------+----------+
Markov Random Field
Markov Random Field (이하 MRF)는 무방향성 그래피컬 모델을 의미합니다. MRF를 사용하는 이유는 아래와 같은 BN으로 표현할 수 없는 독립성을 표현할 수 있기 때문입니다.
\[(A\perp C\vert D,B)\;\mathrm{and}\;(B\perp D\vert A,C)\]이러한 독립성은 아래 MRF를 이용하면 표현가능합니다.
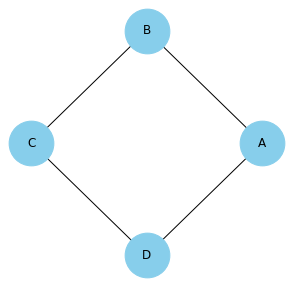
MRF의 각 변은 조건부 확률분포를 나타내지는 않습니다. 따라서, 결합확률분포를 모델링하기 위해서는 다른 접근 방법이 필요한데, 이때 potential function을 이용합니다.
- Clique : 모든 노드가 서로 연결되어 있는 부분그래프(subgraph)
- 위 예시에서는 $(A,B), (B,C)$ 와 같이 각 변이 clique이 됩니다.
Potential function $\phi$ 란, 확률과는 다른 개념으로 각 clique에 대해 특정 실수값을 부여하는 함수를 의미합니다. 이로부터 다음과 같이 결합확률분포를 나타냅니다.
\[P(X_{1},\ldots,X_{n}) = \frac{1}{Z}\prod_{c\in\mathcal{C}} \phi_{c}(X_{c})\]이때 $Z$는 일종의 normalizing factor로, partition function이라고도 부릅니다. Potential function과 partition function은 아래 코드와 같이 나타낼 수 있습니다.
test_mrf = MarkovNetwork([('A','B'), ('B','C'), ('C','D'), ('D','A')])
# Add factors
from pgmpy.factors.discrete import DiscreteFactor
phi1 = DiscreteFactor(['A', 'B'], cardinality=[2, 2], values=[30, 5, 1, 10])
phi2 = DiscreteFactor(['B', 'C'], cardinality=[2, 2], values=[100, 1, 1, 100])
phi3 = DiscreteFactor(['C', 'D'], cardinality=[2, 2], values=[1, 100, 100, 1])
phi4 = DiscreteFactor(['D', 'A'], cardinality=[2, 2], values=[100, 1, 1, 100])
test_mrf.add_factors(phi1, phi2, phi3, phi4)
test_mrf.get_partition_function() # 7201840.0
Markov Independencies of MRF
BN과는 다르게, MRF에서는 separation(NOT d-separation)의 개념을 사용합니다. MRF $H$에서는 방향성이 없기 때문에, 노드집합 $A$에서 $B$로의 경로가 노드집합 $X$에 의해 막혀있다면 $\mathrm{sep}_{H}(A;C\vert X)$ 라고 합니다. 위 예시에서는 $\mathrm{sep}(A;C\vert B,D)$ 가 성립합니다.
Separation으로부터 얻는 모든 독립성에 대한 집합을 $I(H)$ 라고 표기할 수 있고, 이를 Global MI라고 합니다. 위 예시에서 $I(H)$ 는 다음과 같습니다.
\[(A \perp C \mid B, D),(B \perp D \mid A, C),(C \perp A \mid B, D),(D \perp B \mid A, C)\]MRF에서 Markov Blanket은 변으로 연결된 노드들의 집합을 의미합니다. 위 예시의 경우 $MB_{A}=\lbrace B,D\rbrace $ 가 됩니다.
list(test_mrf.markov_blanket('A')) # ['B', 'D']
Local MI는 Markov Blanket으로부터 정의된 모든 독립성들의 집합을 의미합니다. 즉 그래프 $G$에 대해 다음을 의미합니다.
\[I_{l}(G) = \lbrace X_{i}\perp V-\lbrace X_{i}\rbrace -MB_{X_{i}}\mid MB_{X_{i}} :\forall i\rbrace\]Hammersley-Clifford Theorem
확률변수들의 집합 $V=\lbrace X_{1},\ldots,X_{n}\rbrace $ 에 대해 결합확률분포가 strictly positive하고, $V$에 대해 정의된 MRF $H$가 존재할 때, 다음 조건들은 동치입니다.
-
결합확률분포 $P$가 Gibbs distribution을 따른다.
\[P(X_{1},\ldots,X_{n})=\frac{1}{Z}\prod_{c\in\mathcal{C}}\phi_{c}(X_{c})\] -
Local Markov property
\[P(X_{i}\mid \mathbf{X}\backslash\lbrace X_{i}\rbrace )=P(X_{i}\mid MB_{X_{i}})\] -
Global Markov property: 서로소인 노드집합 $A,B,S$에 대해
\[\mathrm{sep}_{H}(A;B\mid S) \Rightarrow P(A\mid S,B)=P(A\mid S)\]가 성립한다.
Minimal I-Map, P-Map
Bayesian Networks
BN $G$가 확률분포 $P$의 minimal I-Map이라는 것은 $G$의 부분그래프(변을 하나 이상 제거한 그래프)가 $P$의 I-map이 되지 못하는 것을 의미합니다. 또한, 모든 확률분포에 대해 minimal I-map은 존재하며, 이는 모든 노드가 연결된 완전그래프로부터 출발하면 찾을 수 있습니다. 다만, minimal I-map은 유일하지 않은데, 이는 노드의 순서를 정의하는 방식에 따라 달라질 수 있습니다.
P-Map 이란, $I(G)=I(P)$ 인 경우를 말합니다. 즉 확률분포에서의 모든 독립 구조와 그래프에서의 모든 독립구조가 일치함을 의미합니다. 이 경우 조건부 독립과 d-separation은 동치가 되며, P-Map은 유일하게 존재합니다. 다만, P-Map이 존재하지 않는 확률분포도 존재합니다.
그래프 $G,G’$ 에 대해 $I(G)=I(G’)$ 가 성립하면 이를 I-equivalent하다고 합니다. BN에 대해서는, 두 그래프가 같은 골격(skeleton)과 같은 v-structure를 가지면 $I(G)=I(G’)$ 가 성립합니다. 그러나 역에 대해서는 다음 성립하지 않는데, 다음 예시가 그렇습니다.
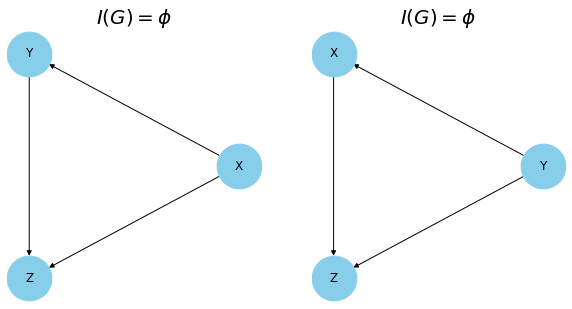
두 그래프는 I-equivalent 하지만, 다른 v-structure를 갖게 됩니다.
V-structure에서 두 부모 노드가 연결되지 않은 경우를 immoral하다고 하는데, I-equivalence를 검정하기 위해서는 immorality에 대해 살펴보아야 합니다. 즉, 다음의 정리가 성립합니다.
$I(G)=I(G’)$ 인 것과 $G,G’$ 가 동일한 골격과 동일한 immoralities 갖는 것은 동치이다.
Markov Random Fields
MRF $H$에 대해 확률분포 $P$가 Gibbs distribution을 갖는다면, $H$는 $P$의 I-map이 됩니다. 또한, MRF에 대해서는 minimal I-map은 유일하게 존재하는데, 이는 Hammersley-Clifford 정리로부터 성립합니다. 만약 $H$가 minimal I-map이 아닌 경우, $H$에는 해당 변을 제거해도 I-map이 되는 변이 존재하는데 HC 정리에 의해 해당 변을 제거하게 되면 확률분포가 변하기 때문입니다.
P-Maps
Immoral한 V-structure의 경우 독립성을 MRF에 표현할 수 없습니다. 이로 인해, 모든 분포가 MRF의 P-map을 갖지는 않습니다. 마찬가지로, 위 예제와 같이 BN으로 표현할 수 없는 독립성이 존재하기 때문에, 모든 분포가 BN의 P-map을 갖지 않습니다.
Conversion
Moral Graph
BN $G$의 moral graph라는 것은, $G$에 속한 모든 v-structure에서 부모 노드들을 연결한 MRF를 의미합니다. 처음 살펴본 student network 예시를 moralize 하면 다음과 같습니다.
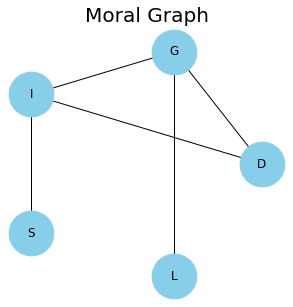
이렇게 만들어진 Moral graph $M(G)$는 BN $G$의 minimal I-map이 됩니다.
Moral graph는 Markov blanket을 쉽게 구할 수 있다는 장점이 있는데, moralize 전의 BN에서 구한 Markov blanket과 moral graph에서 구한 Markov blanket은 일치합니다. 또한, moralize 과정은 각각의 노드에 대해 노드와 부모 노드들을 clique으로 변환한다는 점이 특징입니다. Moral graph에 대해 다음의 정리가 성립합니다.
BN $G$가 moral하다면(v-structure가 없음), moral graph $M(G)$는 $G$의 P-map이다.
또한, BN에서의 d-separation과 moral graph에서의 separation에는 다음 관계가 성립합니다. 여기서 $G^{+}(Z)$ 는 그래프 $G$에서 $Z$의 부모 노드, 조상 노드들로만 구성된 부분그래프를 의미합니다.
\[\text{d-sep}_{G}(X;Y\mid Z)\Leftrightarrow \text{sep}_{M[G^{+}(Z)]}(X;Y\mid Z)\]Triangulation, Chordal Graph
임의의 MRF $H$에 대응하는 minimal I-map인 BN $G$를 찾기 위해서는, triangulation이 필요합니다. Triangulation이란 MRF에 변을 추가하여 최대 clique이 삼각형, 즉 노드 3개로 구성된 clique이 되도록 하는 것입니다. 앞서 살펴본 간단한 MRF에 적용하면 다음 그림과 같습니다.
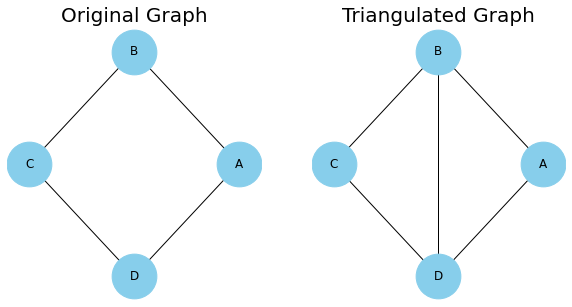
Immoral v-structure는 MRF에서 표현할 수 없기 때문에, triangulation을 이용하여 immorality들을 제거해주는 것입니다.
또한, 위와 같이 MRF 루프 $A-B-C-D$ 에 대해, 루프상 인접하지 않은 $B-D$ 를 연결한 그래프를 Chordal Graph라고 합니다. Chordal graph에 방향성을 부여한 경우 해당 BN 역시 chordal하다고 정의합니다. Chordal graph가 중요한 이유 역시, chordal BN에는 immorality가 존재할 수 없기 때문이며 이를 이용해 MRF에 대한 minimal I-map을 구현할 수 있습니다.
BN $G$가 MRF $H$의 minimal I-map이라면, $G$는 반드시 chordal이어야 한다.
역으로, 다음과 같은 정리도 생각할 수 있습니다.
Non-chordal MRF $H$에 대해서는 P-map인 BN이 존재하지 않는다.
Clique Trees
MRF $H$에 존재하는 clique들을 각각 $D_{1},\ldots, D_{k}$ 라고 두면 각각의 $D_{1},\ldots,D_{k}$ 들을 노드로 하는 트리 형태의 구조를 만들 수 있습니다. 이를 Clique tree(or Junction tree)라고 합니다. 이때 $S_{ij}=D_{i}\cap D_{j}$ , $W_{ij}=D_{i}-S_{ij}$ 라고 정의하면, 위 예시에서는 다음과 같습니다.
\[\begin{align} D_{1}=\lbrace A,B,D\rbrace \\ D_{2}=\lbrace B,C,D\rbrace \\ S_{12}=\lbrace B,D\rbrace \\ \end{align}\]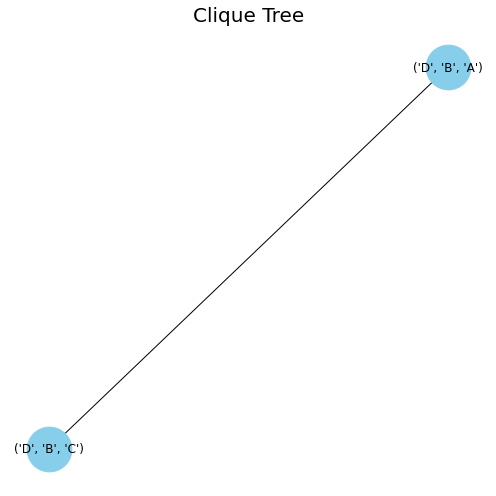
Clique tree는 모든 chordal MRF $H$에 대해 존재하며, clique tree로 부터 $H$의 P-map인 BN을 만들어낼 수 있습니다. 다음과 같은 순서로 진행합니다.
\[\mathrm{Pa}(X_{i}) = (D_{k}-\lbrace X_{i}\rbrace ) \cap \lbrace X_{1},\ldots,X_{i-1}\rbrace\]
- $H$에 triangulation을 적용하여 chordal graph를 만든다.
- Clique tree $T=\lbrace D_{1},\ldots,D_{n}\rbrace $를 구성한다.
- 노드의 순서를 정하고(ex. $A-B-C-D\ldots$), 이에 대응되는 clique들의 순서 역시 설정한다.
- 노드 순서대로 노드 $X_{i}$에 대해 해당 노드가 가장 처음 등장하는 clique을 $D_{k}$라고 한다.
- $X_{i}$의 부모 노드가 아래와 같도록 각 변의 방향을 설정한다.
위 과정을 거치면 P-map인 Bayesian Network을 얻을 수 있습니다. 예시는 다음과 같습니다.
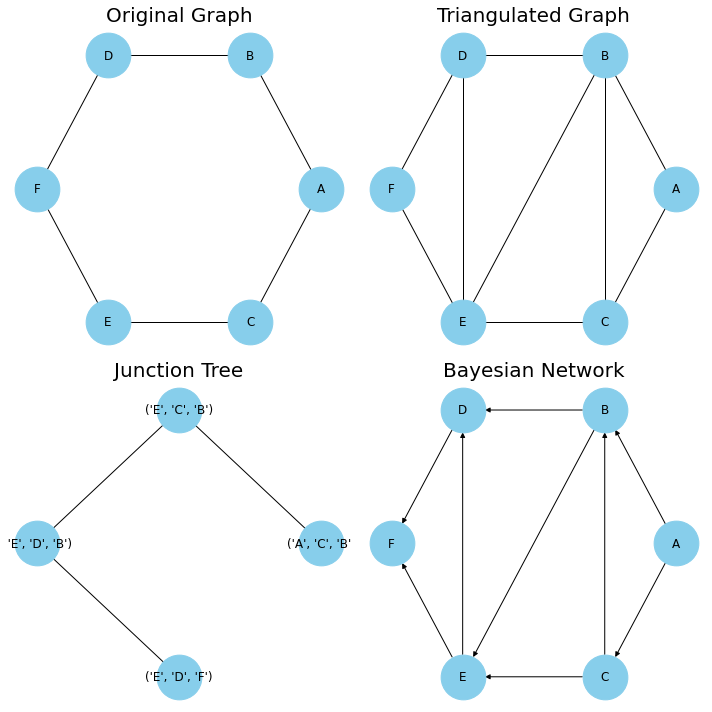
위 예시에서는 노드의 순서가 다음과 같습니다.
\[A - C - B - E - D - F\]References
- https://gist.github.com/naveenrajm7/361a648cfe3e03f0b1e1de7c61281dfa
- Code on Github
Leave a comment