Conformal Prediction

Introduction

일반적으로 통계학에서는 선형모형과 같은 모델을 설정하고, 이를 바탕으로 설명변수와 예측변수 간의 관계를 분석한다. 나아가, 학습한 모델을 바탕으로 새로운 데이터 $x^\ast$가 주어졌을 때, 이에 대한 예측값 $\hat{y}^\ast$를 계산한다. 예를 들어, 데이터 $X=(x_1, x_2, \cdots, x_{n}), Y=(y_{1},\cdots, y_{n})$ 이 주어졌을 때 다음과 같은 단순선형회귀 모형(Simple Linear Regression Model)을 고려하자.

\[y_{i} = \beta_{0} + \beta_{1}x_{i} + \epsilon_{i}, \quad i=1,2,\cdots,n\]

이때 새로운 데이터 $x_{n+1}$에 대한 예측값 $\hat{y}_{n+1}$ 은 다음과 같이 주어지고,

\[\hat{y}_{n+1} = \hat{\beta}_{0} + \hat{\beta}_{1}x_{n+1}\]

예측값에 대한 $100(1-\alpha)\%$ 예측 구간(prediction interval)은 다음과 같이 주어진다.

\[\hat{y}_{n+1} \pm t_{n-2,1-\alpha/2} \times \sqrt{MSE \left(1 + \frac{1}{n} + \frac{(x_{n+1} - \bar{x})^{2}}{\sum_{i=1}^{n}(x_{i} - \bar{x})^{2}}\right)}\]

그러나, 이러한 방법은 앞서 가정한 것과 같이 데이터의 분포에 대한 올바른 가정이 필요하다. 모델이 잘 설정되어 있는 경우(well-specified model)에는 안정적인 예측구간을 제공할 수 있지만, 그렇지 못한 경우에는 구간의 수준이 잘 보장되지 않을 수 있다. (예를 들어, coverage probability가 95%로 설정되어 있지만, 실제로는 90%일 수 있다.) 다음과 같은 데이터 생성 메커니즘에 대해 단순 선형회귀모형 $y=\beta_0+\beta_1 x$ 을 사용할 경우, 신뢰구간이 잘못 설정될 수 있다. 아래 그림의 빨간색 구간은 단순선형모형에 대한 예측구간을 나타내고, 올바른 모형인 2차 다항회귀모형에 대한 예측구간은 파란색 구간으로 나타내어져 있다.

\[Y = 5 + 2X + \frac{1}{2}X^{2} + N(0,2^{2})\]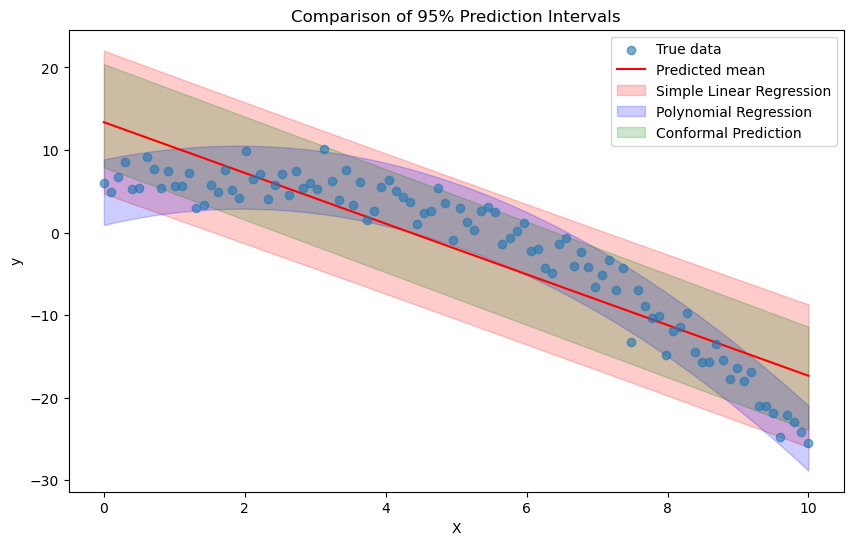

Conformal prediction은 이러한 문제점을 가지고 있지 않은데 (위 그림의 초록색 구간), 이는 예측 구간을 모델 가정 없이 제공한다는 점으로부터 나온다. 앞선 예시처럼 일변수 모델이나 변수의 관계를 파악하기 쉬운 경우에는 상관이 없을 수 있지만, 일반적으로 복잡한 데이터에 대해 예측을 수행하는 경우 올바른 모델을 상정하는 것이 어렵기 때문에 Conformal Prediction은 유용하게 사용된다. 물론 올바른 모델을 상정하는 것이 가능하다면, 이를 사용하는 것이 더 좋을 수 있다 (파란색 구간과 초록색 구간의 비교).

Definition

이번 글의 내용은 “A Gentle Introduction to Conformal Prediction and Distribution-Free Uncertainty Quantification” paper에 기반하여 작성되었다. 우선, 분류 문제를 기반으로 Conformal Prediction에 대한 정의를 살펴보자.

$K$개 클래스를 분류하는 문제를 (ex. MNIST) 고려하자. $X$를 설명변수, $Y$를 예측변수로 하여, $\mathbf{X}=(X_1,X_n \cdots,X_n)$, $Y=(y_1, y_2, \cdots, y_n)$ 이 주어졌을 때, 새로운 테스트 데이터 $X_{\mathrm{test}}$ 에 대한 예측 집합(Prediction set)은 다음과 같이 정의된다.

\[1-\alpha \le P(Y_{\mathrm{test}} \in \mathcal{C}(X_{\mathrm{test}})) \le 1 - \alpha + \frac{1}{n+1}\]

이러한 정의를 만족시키는 집합 $\mathcal{C}(X_{\mathrm{test}})$을 valid한 prediction set이라고 한다. 이때, $\alpha$는 오류율을 의미하며, 이러한 성질을 marginal coverage라고 한다. 여기서 marginal의 의미는 위 정의의 확률이 random하게 선택된 $X_{\mathrm{test}}, Y_{\mathrm{test}}$에 대해서만 성립한다는 것을 의미한다 (임의로 선택한 예측 지점 $X_\ast$에 대해서는 성립하지 않는다).

Exchangeability

Conformal prediction은 모델 가정을 이용하지는 않는다. 그럼에도 conformal prediction이 이루어지기 위해서는 교환가능성(exchangeability) 이라는 가정이 필요한데, 이는 주어진 데이터가 순서를 바꾸어도 동일한 joint distribution을 가진다는 가정이다. 따라서, 일반적으로 통계학에서 많이 사용되는 가정인 i.i.d. 가정은 당연히 교환가능성을 만족한다. 시계열 자료나 공간성 자료를 제외할 경우에는 일반적으로 i.i.d. 가정을 상정하는 것이 어려운 일이 아니기 때문에, 그보다 더 약한 가정인 교환가능성은 충분히 만족할만한 가정이다.

How to Make a Prediction Set?

그렇다면, 교환가능성이 주어질 때 어떻게 예측집합 $\mathcal{C}$를 구성할 수 있을지 살펴보자. 우선, conformal prediction을 위해서는 nonconformality measure (혹은 conformal score) 라고 하는 측도 $s(x,y)$ 가 필요하다. 이는 설명변수 $x$와 반응변수 $y$간의 불일치 정도를 측정하는 측도로, $s(x,y)$ 값이 클수록 $x$와 $y$가 잘 맞지 않는 것을 의미한다.

Conformal prediction의 또 하나의 특징이자 장점은, 앞서 정의한 nonconformity measure를 사용할 때 어떤 종류의 측도를 사용하던 상관이 없다는 것이다. 예컨대, 회귀분석의 경우 OLS 선형모형을 만들어 다음과 같은 residual

\[s(x_{i},y_{i}) = \left\vert \frac{y_{i} - \hat \mu(x_{i}) }{\hat \sigma(x_{i})}\right\vert\]

를 사용하거나, 혹은 복잡한 딥러닝 모델 $f$를 바탕으로 잔차를 계산해도 된다. 분류 문제의 경우, 실제 클래스에 대한 예측 확률을 1에서 빼거나 부호를 바꾸어 실제 클래스와의 불일치성을 측정할 수 있다. 즉, nonconformity 를 측정할 수 있다는 의미만 내포한다면, 모형과 형태에 관계없이 어떠한 측도든 사용가능하다는 특징이 있다. 따라서 conformal prediction에서는 일반적으로 계산이 빠르고 간편한 모델을 사용하는 것이 선호되기도 한다.

다음으로, 주어진 데이터 $(X_{1},y_{1}),\ldots (X_{n},y_{n})$ 각각에 대해 nonconformity score를 계산한다. 즉, $s_{1}=s(X_{1},y_{1}),\ldots, s_{n}=(X_{n},y_{n})$ 을 얻게 된다. 이후 우리가 알고자 하는 신뢰수준 $\alpha$에 대해, $s_{1},\ldots s_{n}$ 의 $\frac{\lceil (n+1)(1-\alpha)\rceil}{n}$ 분위수 $\hat q$를 계산한다.

\[\hat q = \inf\left\{ q : \frac{|\{i:s(X_{i},y_{i})\le q\}|}{n}\ge \frac{\lceil (n+1)(1-\alpha)\rceil}{n}\right \}\]

결과적으로 이렇게 얻은 분위수 $\hat q$를 이용하여 다음 예측 집합을 구성할 수 있다.

\[\mathcal{C}(X_{\mathrm{test}}) = \{ y: s(X_\mathrm{test}, y) \le \hat q \}\]

만일 회귀문제에서 잔차 측도를 사용하였다면, 예측 집합은 $[y_{\mathrm{test}} - \hat q \hat \sigma(X_{\mathrm{test}}), y_{\mathrm{test}} + \hat q \hat \sigma(X_{\mathrm{test}})]$ 의 구간으로 나타낼 수 있다. 이러한 집합은 다음 정리에 의해 앞서 언급한 validity(타당성)을 만족한다.

Theorem (Conformal coverage guarantee, Vovk et al.)

데이터 $(X_{i},y_{i})_{i=1,\ldots, n}$ 와 예측 대상 데이터 $(X_{n+1},y_{n+1})$ 이 교환가능하다고 하자. 위 과정과 같이 $\hat q$를 계산하고, 이를 바탕으로 예측 집합 $\mathcal{C}(X_\mathrm{test})$ 을 만들었다면, 다음이 성립한다.

\[P(Y_\mathrm{test} \in \mathcal{C}(X_\mathrm{test})) \ge 1- \alpha\]

또한, 만일 score $s_{1},\ldots, s_{n}$ 들의 분포가 연속형(continuous) 이라면, 다음이 성립한다.

\[P(Y_\mathrm{test} \in \mathcal{C}(X_\mathrm{test})) \ge 1- \alpha + \frac{1}{n+1 }\]

이렇게만 보면, conformal prediction은 일반적인 모델 기반 예측보다 매우 쉽고 간편하면서도 좋은 성능을 보인다고 생각할 수 있다. 그러나 직관적으로도 알 수 있듯이, 앞서 언급한 nonconformity score를 채택하는 문제가 매우 중요하다. 측도의 종류에 따라 예측 집합의 성능이 천차만별일 수 있고, 특히 문제 상황별로 요구될 수 있는 측도가 다를 수 있는 것도 고려해야할 점이다. 다음으로는 이를 응용한 Conformalized Quantile Regression에 대해 살펴보도록 하겠다.

Conformalized Quantile Regression

Quantile Regression

첫번째 예시는 회귀 문제에서 quantile regression^{분위수 회귀}에 conformal predicton을 적용한 conformalized quantile regression이다. Quantile regression은 제곱오차를 최소화하는 대신, pinball loss function $\rho_{\alpha}$을 도입해 다음의 문제를 최적화한다.

\[\hat \theta = \arg\min_{\theta} \frac{1}{n} \sum_{i=1}^{n}\rho_{\alpha}(Y_{i}-f(X_{i};\theta))+R(\theta)\]

여기서 $f(X;\theta )$ 는 회귀모형, $R(\theta)$는 규제항을 각각 나타낸다. 이때 pinball loss는 다음과 같다.

\[\rho_{\alpha}(y, \hat y) := \begin{cases} \alpha (y-\hat y) & \text{if } y-\hat y >0 \\ (1-\alpha)(\hat y-y) &\text{o.w.} \end{cases}\]

조건부 분위수 함수(conditional quantile function) 을 다음과 같이 정의하면,

\[q_{\alpha}(x) := \inf\{y\in \mathbb{R}: F(y|X=x) \ge \alpha \}\]

적당한 조건 하에서 $\hat q_{\alpha}(x)= f(x;\hat \theta)$ 가 위 조건부 분위수 함수로 수렴하는 것이 알려져 있다 (Consistency). 분위수 회귀분석을 $\frac{\alpha}{2}$, $1- \frac{\alpha}{2}$ 분위수에 적용시킨다면 다음과 같이 $100(1-\alpha)$% coverage 를 갖는 에측 구간 추정치를 얻을 수 있다.

\[\hat C(X_{n+1}) = [\hat q_{\alpha / 2}(X_{n+1}), \hat q_{1 - \alpha/2}(X_{n+1})]\]

Conformalized quantile regression은 이러한 아이디어로부터 출발한다.

Conformalized Quantile regression (CQR)

데이터셋 $D = {(X_{i},y_{i}) : i=1,\ldots n } $ 이 주어졌을 때, 주어진 데이터셋 $D$를 training dataset $I_{1}$ 과 calibration set $I_{2}$ 로 분리하자 (scikit-learn의 train_test_split 을 이용해 데이터셋을 나눈다고 생각하면 됨). 우선 training set $I_{1}$의 데이터를 바탕으로 앞서 살펴본 quantile regression algorithm $\mathcal{A}$를 적합한다. Coverage level $100(1-\alpha)$% 에 대해 다음 두 개의 조건부 분위수 함수를 적합한다.

\[\{\hat q_{\alpha / 2}, \hat q_{1 - \alpha/2} \} \leftarrow \mathcal{A}(\{(X_{i},y_{i}):i\in I_{1} \} )\]

다음으로는, conformal prediction을 수행하기 위해 nonconformity measure를 정의해야 하는데, 여기서는 다음과 같은 측도를 정의한다.

\[E_{i} := \max \{\hat q_\frac{\alpha}{2} (X_{i}) -Y_{i}, Y_{i}-\hat q_{1 - \frac{\alpha}{2}}(X_{i})\}\]

만일 실제 값 $Y_{i}$가 예측구간보다 아래 위치한다면

\[E_{i}=|Y_{i}-\hat q_{\frac{\alpha}{2}}(X_{i})|\]

가 되는데, 이는 실제 값과 예측값의 nonconformity를 나타낸다는 측면에서 이치가 맞는 측도라고 볼 수 있다. 이를 바탕으로 또 다른 분위수 (여기서는 conformal prediction set을 위한 분위수를 말한다) $Q_{\alpha}(E, I_{2})$ 를 계산한다. 이는 calibration set 데이터들의 score $E_{1},\ldots E_{n_{\mathrm{cal}}}$ 들의 $(1-\alpha)(1+1/|I_{2}|)$ 번째 분위수로 주어지며, 이를 바탕으로 최종적인 예측집합을 구성할 수 있다.

\[C(X_{n+1}) = [\hat q_{\alpha / 2}(X_{n+1})-Q_{1-\alpha}(E,I_{2}), \hat q_{1 - \alpha/2}(X_{n+1})+Q_{1-\alpha}(E,I_{2})]\]

요약하자면, 분위수 회귀분석의 아이디어를 차용하여 1차적인 예측집합을 만든 후 이를 바탕으로 nonconformity measure를 새롭게 정의했음을 확인할 수 있다. 분위수 회귀도 복잡한 머신러닝 모델들에 비해 간편하기 때문에, 마찬가지로 계산에 소요되는 시간이 적어 적합한 모델이라고 할 수 있다.

Note. Calibration set $I_{2}$ 의 모든 data point에 대해 nonconformity measure $E_{i}$ 를 측정해야 하므로, 모델 훈련의 속도보다 evaluation (prediction) 의 속도가 conformal prediction의 컨텍스트에서는 더 중요하다고 할 수 있다.

Python Code

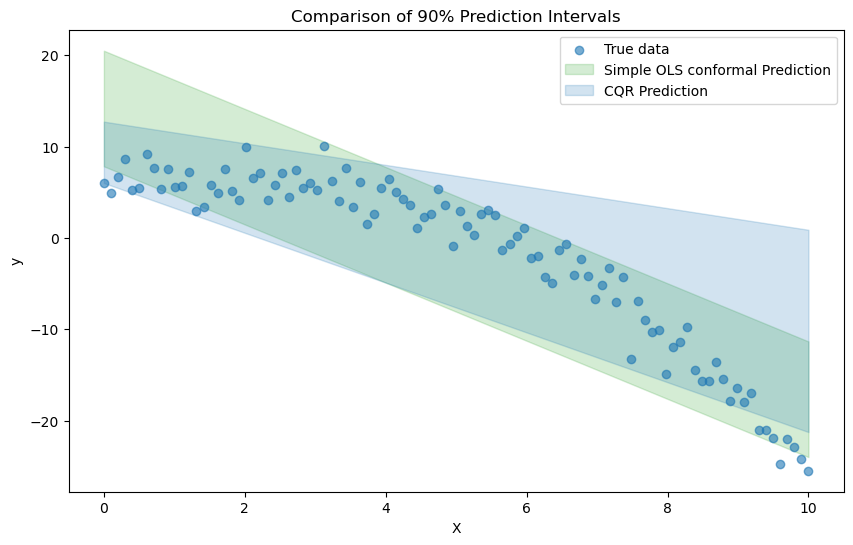
아래 결과는 도입부의 예시 데이터에 대해 단순선형회귀 residual을 기반으로 한 conformal prediction의 예측집합과 CQR의 예측집합을 비교한 것이다 ($\alpha=0.1$).

# Conformalized Quantile Regression
from sklearn.linear_model import QuantileRegressor, LinearRegression

## Make qunatile regression model
X_train, X_calib, y_train, y_calib = train_test_split(X, y, test_size=0.2, random_state=42)

alpha = 0.1
quantile_model_lo = QuantileRegressor(alpha=alpha/2, solver='highs')
quantile_model_lo.fit(X_train, y_train)

quantile_model_hi = QuantileRegressor(alpha=1-alpha/2, solver='highs')
quantile_model_hi.fit(X_train, y_train)

## Make Linear regression model
linear_model = LinearRegression()
linear_model.fit(X_train, y_train)

# Get nonconformity scores on calibration set
calib_preds_lo = quantile_model_lo.predict(X_calib)
calib_preds_hi = quantile_model_hi.predict(X_calib)


nonconformity_score = np.maximum(calib_preds_lo - y_calib, y_calib - calib_preds_hi)

# Compute quantile for residuals
n_calib = len(y_calib)
Q = np.quantile(nonconformity_score, (1-alpha)*(1+1/n_calib))

# Generate conformal prediction intervals
X_test = np.linspace(0, 10, 20).reshape(-1, 1)
test_preds_lo = quantile_model_lo.predict(X_test)
test_preds_hi = quantile_model_hi.predict(X_test)

cqr_lower = test_preds_lo - Q
cqr_upper = test_preds_hi + Q

# Plot cqr prediction intervals vs conformal prediction intervals for linear regression

plt.figure(figsize=(10, 6))
plt.scatter(X, y, label="True data", alpha=0.6, zorder = 5)
plt.fill_between(np.linspace(0,10,20), conformal_lower, conformal_upper, color='tab:green', alpha=0.2, label="Simple OLS conformal Prediction")
plt.fill_between(np.linspace(0,10,20), cqr_lower, cqr_upper, color='tab:blue', alpha=0.2, label="CQR Prediction")
plt.title("Comparison of 90% Prediction Intervals")
plt.xlabel("X")
plt.ylabel("y")
plt.legend()
plt.show()

References

A. N. Angelopoulos and S. Bates, “A Gentle Introduction to Conformal Prediction and Distribution-Free Uncertainty Quantification,” Dec. 07, 2022, arXiv: arXiv:2107.07511. doi: 10.48550/arXiv.2107.07511.
K. P. Murphy, Probabilistic machine learning: advanced topics. in Adaptive computation and machine learning series. Cambridge, Massachusetts: The MIT Press, 2023.
Y. Romano, E. Patterson, and E. Candes, “Conformalized Quantile Regression,” in Advances in Neural Information Processing Systems, Curran Associates, Inc., 2019. Accessed: Dec. 13, 2024. [Online]. Available: https://proceedings.neurips.cc/paper_files/paper/2019/hash/5103c3584b063c431bd1268e9b5e76fb-Abstract.html