Differential Privacy for Functions

Differential Privacy

Setting

$D=(d_{1},\ldots,d_{n})\in \mathcal{D}$을 입력 데이터베이스라고 하자. 또한, $M:\mathcal{D} \to \mathbb{R}^{d}$를 non-private 알고리즘이라고 하고, $M(D)$를 그에 대응하는 출력이라고 하자. 그러면, 출력 공간 (e.g. $\mathbb{R}^{d}$)을 고려하여, 랜덤화된 메커니즘은 분포 $\lbrace P_{D}:D\in \mathcal{D}\rbrace $로 특성화할 수 있다. $\Omega$를 $\sigma$-field $\mathcal{F}$가 부여된 공간이라고 하자. 그러면, 우리는 분포에 대한 DP를 정의할 수 있다.

Definition

분포들의 집합 $\lbrace P_{D}:D\in\mathcal{D}\rbrace $은 다음 조건을 만족하면 $(\epsilon,\delta)$-DP를 만족한다고 한다.

\[P_{D}(A) \le e^{\epsilon}P_{D'}(A) + \delta,\quad \forall A\in\mathcal{F}\tag{1}\]

여기서 $\mathcal{F}$는 $P_{D}$가 정의되는 가장 작은 $\sigma$-field이다.

Sigma-field of DP algorithm

$\sigma$-field $\mathcal{F}$ 은 DP 알고리즘에서 중요한 역할을 한다.

• $\mathcal{F}=\lbrace \Omega,\phi\rbrace $이면 조건 $(1)$은 자명하게 만족된다.
• 따라서 $\Omega$가 이산적일 때, 일반적인 $\sigma$-필드는 $\mathcal{F}=2^{\Omega}$이다.
• $\Omega$가 위상 공간일 때, $\mathcal{F}=\mathcal{B}(\mathbb{R}^{d})$ (Borel $\sigma$-field)이다.

이 논문에서, $\Omega$는 함수의 공간, 즉 무한 차원 벡터 공간으로 간주된다.

DP on Finite Dimensional Vector space

유한차원 벡터공간에서는 sensitivity $\Delta$ 가 유계이도록 할 수 있기 때문에, 이를 이용해 DP를 정의할 수 있다.

Lemma

모든 이웃 데이터셋 $D\sim D’$에 대해 다음을 만족하는 집합 $A^{\ast}_{D,D’}\in \mathcal{F}$ 이 존재한다고 하자.

\[S\subseteq A^{\ast}_{D,D'}\Rightarrow P_{D}(S) \le e^{\epsilon}P_{D'}(S),\quad \forall S\in\mathcal{F}\tag{2}\]

이고

\[P_{D}(A^{\ast}_{D,D'})\geq 1-\delta\]

그러면 분포족 $\lbrace P_{D}\rbrace $은 $(\epsilon,\delta)$-DP를 만족한다.

Remark

만일 $(\Omega,\mathcal{F})$이 $\sigma$-finite인 지배측도 $\lambda$를 가지면, $(2)$의 충분조건을 만족시키기 위한 조건은 다음과 같다.

\[\forall a\in A_{D,D'}^{\ast} : \frac{dP_{D}}{d\lambda}(a) \le e^{\epsilon}\frac{dP_{D'}}{d\lambda}(a).\]

이는 다음 부등식으로부터 성립한다.

\[P_{D}(S) = \int_{S}\frac{dP_{D}}{d\lambda}(a)d\lambda(a)\le \int_{S}e^{\epsilon}\frac{dP_{D'}}{d \lambda}(a)d\lambda(a)=e^{\epsilon}P_{D'}(S)\]

Proposition

정부호 대칭행렬 $M\in \mathbb{R}^{d\times d}$에 대해, 벡터들의 모임 $\lbrace v_{D}:D\in \mathcal{D}\rbrace \subset \mathbb{R}^{d}$이 다음을 만족하고

\[\sup_{D\sim D'} \left\Vert M^{-\frac{1}{2}}(v_{D}-v_{D'})\right\Vert_{2}\le \Delta\]

입력 데이터 $D$를 갖는 랜덤화된 알고리즘이 다음 출력을 생성한다고 하자.

\[\tilde v_{D} = v_{D} + \frac{c(\delta)\Delta}{\epsilon}Z,\quad Z\sim \mathcal{N}(0,M)\]

그러면 해당 알고리즘은 다음 조건 하에서 $(\epsilon,\delta)$-DP를 만족한다.

\[c(\delta) \ge \sqrt{2\log \frac{2}{\delta}}.\]

여기서 $\Delta$는 Mahalanobis 거리로 측청된 민감도라고 볼 수 있으며, $M=I$인 경우는 (McSherry & Mironov, 2009)에서 사용한 유클리드 거리를 나타낸다.

Implication

프라이버시를 보호한다는 관점에서, 상대방^adversary이 알고 있는 데이터베이스를 $D_{A}$라고 하자. 이때, $D_{A}=(d_{1},\ldots d_{n-1})$ 이고, 프라이버시를 보호하는 데이터베이스를 $D=(d_{1},\ldots,d_{n})$라고 하자. 이 경우 상대방은 $D_{A}\cup\lbrace d\rbrace =D$라고 생각할 수 있다. 이러한 상황에서 다음 명제가 성립한다.

Proposition

$X\sim P_{D}$이고 $P_{D}$가 $(\epsilon,\delta)$-DP를 만족한다고 하자. 그러면 $H=D=D_{0} \text{ vs } V:D\neq D_{0}$의 유의수준 $\gamma$의 검정의 검정력은 $\gamma e^{\epsilon}+\delta$ 보다 작거나 같다.

해당 검정은 공간에서 가측집합이므로, DP의 제약 조건이 유지된다.

DP on the Function space

$T=\mathbb{R}^{d}$에서의 함수 모임을 다음과 같이 고려하자.

\[{f_{D}:D\in \mathcal{D}} \subset \mathbb{R}^{T}\]

랜덤화된 메커니즘은 입력 $D$를 받아서 $\tilde f_{D}\sim P_{D}$를 출력한다. 여기서 $P_{D}$는 $D$에 대응하는 $\mathbb{R}^{T}$에서 measurable한 분포이다.

Field of Cylinders

모든 유한 부분집합 $S=(x_{1},\ldots,x_{n})$ of $T$와 Borel 집합 $B\in \mathcal{B}(\mathbb{R}^{n})$에 대해 함수의 cylinder 집합을 다음과 같이 정의하자.

\[C_{S,B}={ f\in \mathbb{R}^{T}:(f(x_{1}),\ldots,f(x_{n}))\in B}.\]

그러면 집합들의 모임

\[\mathcal{C}_{S}={C_{S,B}:B\in \mathcal{B}(\mathbb{R}^{n})}\]

은 각 고정된 $S$에 대해 $\sigma$-field를 형성한다.

또한, 모든 유한 집합 $S$에 대한 합집합

\[\mathcal{F}_{0}=\bigcup_{S:\left\vert S\right\vert<\infty} \mathcal{C}_{S}\]

은 field이지만, $\sigma$-field는 아니다 (Billingsley, 1995).

DP

$S\subset T$는 $\mathcal{C}_{S}\subset \mathcal{F}{0}$를 의미하므로, 다음이 성립할 때마다

\[P(\tilde f_{D}\in A)\le e^{\epsilon}P(\tilde f_{D'}\in A) + \delta,\quad \forall A\in \mathcal{F}{0}\]

다음 벡터

\[\left(\tilde f{D}(x_{1}),\ldots, \tilde f_{D}(x_{n})\right)\]

를 releasing하는 것은 $(\epsilon,\delta)$-DP를 만족한다.

참고

\[P_{D}\left(\left(\tilde f(x_{1}),\ldots, \tilde f(x_{n})\right)\in A\right) = P_{D}(\tilde f \in C_{\lbrace x_{1},\ldots,x_{n}\rbrace ,A}\]

$\mathcal{F}{0}$는 $\sigma$-field가 아니므로, 다음과 같이 생성된 $\sigma$-field를 고려하자.

\[\mathcal{F} := \sigma(\mathcal{F}_{0}) = \bigcup_{S}\mathcal{C}_{S}\]

여기서 $S$는 $T$의 가산 부분집합이다. 그러면, 가산 집합 $S$에 대해, cylinder 집합은 다음과 같은 형태를 가진다.

\[C_{S,B}=\lbrace f\in \mathbb{R}^{T}:f(x_{i})\in B_{i},i=1,2,\ldots\rbrace = \bigcap_{i=1}^{\infty}C_{\lbrace x_{i}\rbrace ,B_{i}}\]

여기서 $B_{i}\in\mathcal{B}(\mathbb{R})$이다. 또한, 이로부터 DP의 정의를 다음과 같이 쓸 수 있다.

\[P_{D (A)}\le e^{\epsilon}P_{D'}(A) + \delta,\quad \forall A\in \mathcal{F}\]

Gaussian Process Noise

Definition

$T$에 의해 인덱싱된 가우시안 프로세스^{Gaussian Process, GP}는 각각의 유한 부분집합이 다변량 가우시안 분포를 갖는 확률변수들의 집합(process) $\lbrace X_{t}:t\in T\rbrace $이다. 가우시안 프로세스에서의 sample은 함수 $T\to \mathbb{R}$를 의미한다(sample function).

GP는 다음과 같은 mean function, covariance function으로 정의된다.

\[m(t) =\mathrm{E}X_{t},\quad K(s ,t) = \mathrm{Cov}(X_{s},X_{t})\]

즉, 유한부분집합으로 정의되는 분포는 다음과 같이 정의된다.

\[\lbrace X_{t}:t\in S\rbrace \sim \mathcal{N}(m(t),K)\]

이렇게 유한부분집합 $S$에 의해 정의되는 다변량 정규분포를 projection으로도 볼 수 있다.

Proposition

$G\sim GP(0,K)$ 이라고 하자. $M$은 Gram matrix를 의미하고, 집합 $\lbrace f_{D}:D\in \mathcal{D}\rbrace $은 입력 데이터베이스로 인덱싱된 함수들의 모임이라고 하자. 그러면 다음 함수의 releasing은

\[\tilde f_{D}=f_{D}+ \frac{\Delta c(\delta)}{\epsilon}G\]

cylinder $\sigma$-field $\mathcal{F}$에 대해 아래 조건 하에서 $(\epsilon,\delta)$-DP를 만족한다.

\[\sup_{D\sim D'} \sup_{n}\sup_{\lbrace x_{1},\ldots,x_{n}\rbrace \in T^{n}} \left\Vert M^{- \frac{1}{2}}(x_{1},\ldots,x_{n}) \begin{pmatrix}f_{D}(x_{1})-f_{D'}(x_{1}) \\ \vdots \\ f_{D}(x_{n})-f_{D'}(x_{n})\end{pmatrix} \right\Vert_{2}\leq \Delta\]

Proof. See p.713

RKHS

RKHS에 대한 내용은 다음 포스트를 참고하자.

Proposition

RKHS $H$와 대응하는 kernel $K$에 대해, $f\in H$이고 $x_{1},\ldots,x_{n}$이 $T$의 서로 다른 점이라고 하자. 그러면 다음이 성립한다.

\[\left\Vert \begin{pmatrix} K(x_{1},x_{1})&\cdots & K(x_{1},x_{n}) \\ \vdots & \ddots &\vdots \\ K(x_{n},x_{1}) & \cdots & K(x_{n},x_{n})\end{pmatrix}^{-\frac{1}{2}} \begin{pmatrix}f(x_{1}) \\ \vdots \\ f(x_{n})\end{pmatrix} \right\Vert_{2} \le \left\Vert f\right\Vert_{H}\]

Corollary

데이터셋 $D\in\mathcal{D}$와 Hilbert space의 부분집합 $\lbrace f_{D}:D\in \mathcal{D}\rbrace \subseteq H$를 고려하자. 그러면 다음 함수의 releasing은

\[\tilde f_{D} = f_{D} + \frac{\Delta c(\delta)}{\epsilon}G\]

아래 조건 하에서 cylinder $\sigma$-field에 대해 $(\epsilon,\delta)$-DP를 만족한다.

\[\Delta \geq \sup_{D\sim D'}\Vert f_{D}-f_{D'}\Vert_{H}\]

Example

Kernel Density Estimation

$D$를 $f$를 밀도함수로 갖는 분포에서 추출된 점들의 집합이라고 하자. 가우시안 커널을 사용한 KDE $f_{D}$는 다음과 같이 정의된다.

\[f_{D}(x) = \frac{1}{n(2\pi h^{2})^{\frac{d}{2}}}\sum_{i=1}^{n}\exp \left(\frac{-\left\Vert x-x_{i}\right\Vert_{2}^{2}}{2h^{2}}\right),\quad x\in T\]

$D\sim D’$ 이고 $D’=x_{1},\ldots,x_{n-1},x_{n’}$라고 하자. 그러면 다음이 성립한다.

\[(f_{D}-f_{D'})(x) = \frac{1}{n(2\pi h^{2})^{\frac{d}{2}}}\left(\exp \left(- \frac{\left\Vert x-x_{n}\right\Vert_{2}^{2}}{2h^{2}}\right)-\exp \left(- \frac{\left\Vert x-x_{n}'\right\Vert_{2}^{2}}{2h^{2}}\right)\right)\]

따라서, RKHS 노음은 다음과 같이 upper bound를 가진다.

\[\left\Vert f_{D}-f_{D'}\right\Vert_{H}^{2}\le 2\left(\frac{1}{n(2\pi h^{2})^{\frac{d}{2}}}\right)^{2}.\]

만일 다음과 같이 함수 $\tilde f_{D}$를 releasing한다면

\[\tilde f_{D}=f_{D}+ \frac{c(\delta)\sqrt{2}}{\epsilon n(2\pi h^{2})^{\frac{d}{2}}}G\]

이는 $(\epsilon,\delta)$-DP를 만족한다. 여기서 $G\sim GP(0,K)$이다.

Risk

Non-private KDE의 risk는 다음과 같이 구할 수 있다.

\[\begin{align} h &\asymp \left(\frac{1}{n}\right)^{\frac{1}{4+d}}\\ R &=O(n^{- \frac{4}{4+d}}) \end{align}\]

DP를 고려한 경우, risk는 다음과 같이 구할 수 있다.

\[\mathrm{E}\int \left(\tilde f_{D}(x)-f(x)\right)^{2}dx = O \left(h^{4}+ \frac{c_{2}}{nh^{d}}\right)\]

주목할 것은, rate of convergence 측면에서, 정확성이 손실되지 않았다는 것이다. 아래 그림은 DP가 적용되지 않은 경우와 적용된 경우를 비교한 것이다.

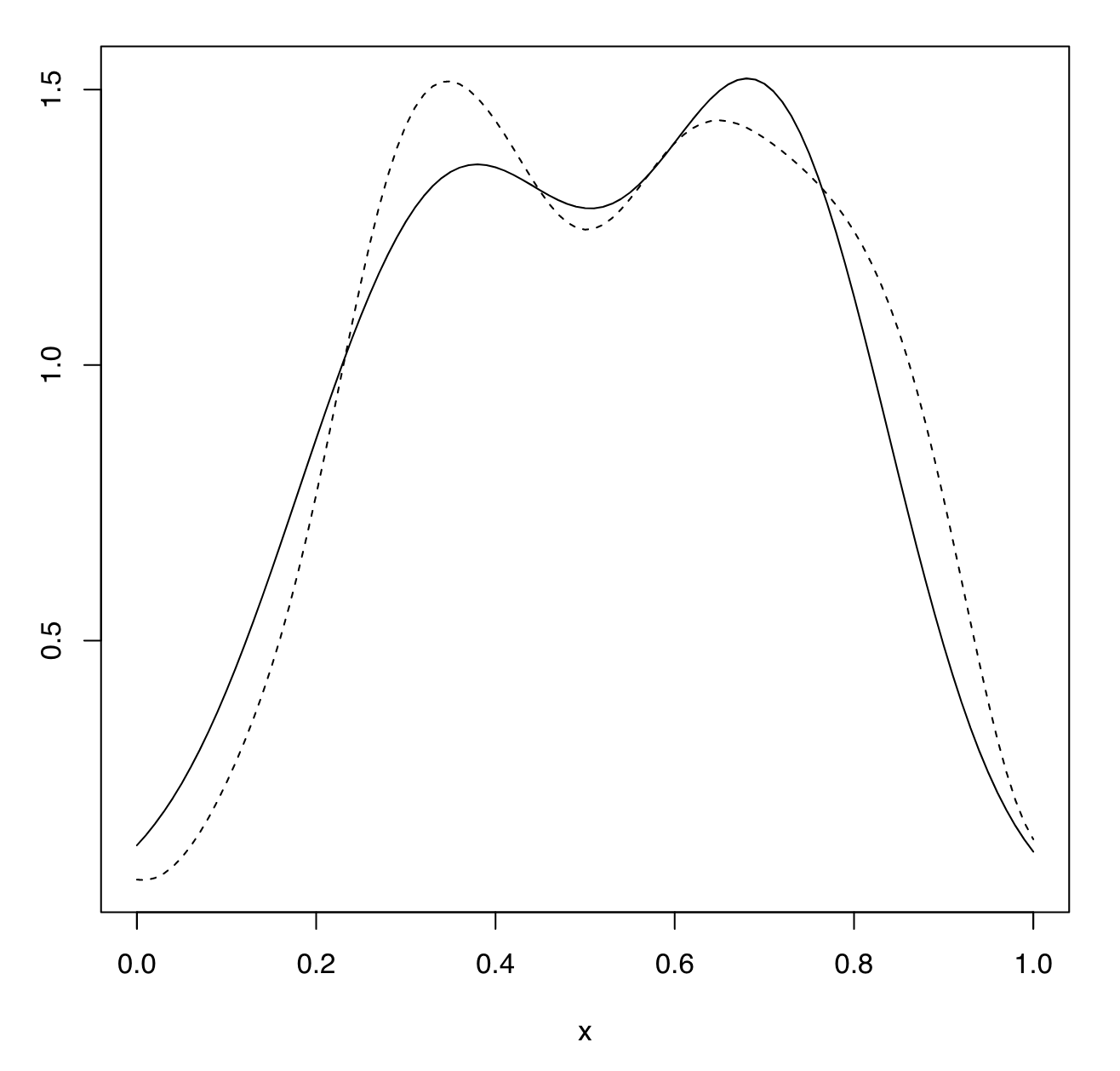Non-private KDE(실선) vs Private KDE(점선)

Optimal bandwidth for DP

• KDE에서 optimal bandwidth를 구하는 과정은 대개 LOOCV^{Leave-one-out-Cross-Validation}를 사용한다.
• 다만, DP를 고려할 경우 $T$가 compact set이라는 가정이 필요하다.

• 이러한 가정이 없는 경우, 다음과 같은 rule of thumb을 사용할 수 있다.

  \[\hat h = \left( \frac{4}{(d+1)n}\right)^{\frac{1}{d+4}} \frac{\mathrm{IQR}_{j}}{1.34}\]

  여기서 $\mathrm{IQR}_{j}$는 $j$번째 변수의 interquartile range이다.

References

• Hall, R., Rinaldo, A., & Wasserman, L. (n.d.). Differential Privacy for Functions and Functional Data.
• Billingsley, P. (1995). Probability and Measure. Wiley.
• McSherry, F., & Mironov, I. (2009). Differentially private recommender systems: Building privacy into the Netflix Prize contenders. Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 627–636. https://doi.org/10.1145/1557019.1557090