Deep Learning with Differential Privacy

DL with DP

이번 포스트에서는 Deep Learning with Differential Privacy (Abadi et al., 2016) 논문을 리뷰하고자 합니다. 이 논문은 neural network 기반의 딥러닝 모델을 Differential Privacy를 만족하도록 학습하는 방법을 제시합니다. 이 과정에서 Stochastic gradient descent (SGD) 자체가 DP를 만족하도록 하는 방법인 DP-SGD를 제시하고, 이는 여러 후속 연구에서도 많이 활용되고 있습니다.

Definitions

Differential Privacy

Randomized mechanism^algorithm $\mathcal{M}:\mathcal{D}\to \mathbb{R}$ 이 데이터셋의 정의역 $\mathcal{D}$ 와 output range $\mathcal{R}$ 를 갖는다고 하자. 이때 메커니즘 $\mathcal{M}$ 이 $(\epsilon,\delta)$-DP인 것은 임의의 두 이웃하는 데이터셋 $D,D’\in\mathcal{D}$ 에 대해

\[\Pr (\mathcal{M}(D)\in S) \le e^{\epsilon}\Pr (\mathcal{M}(D')\in S)+\delta\]

$\forall S\subseteq \mathbb{R}$ 에 대해 성립한다는 것이다. 여기서 $\epsilon$ 은 privacy budget, $\delta$ 는 failure probability이다. 이때 $\delta=0$ 이면 $\epsilon$-DP라고 한다.

$(\epsilon,\delta)$-DP 메커니즘으로 deterministic한 실함수 $f:\mathcal{D}\to \mathbb{R}$ 를 근사하는 일반적인 메커니즘은 Gaussian mechanism이다. 이는 다음과 같이 함수에 Gaussian noise를 추가하는 것이다.

\[\mathcal{M}(D) := f(D) + \mathcal{N}(\mathbf{0},S_{f}^{2}\cdot \sigma^{2}\mathbf{I})\]

여기서 $S_{f}$는 sensitivity^민감도로 정의되며, $\left\vert f(D)- f(D’)\right\vert$로 표현된다. $\sigma$는 noise의 scale을 나타낸다.

DP에 대한 자세한 내용은 Differential Privacy, Renyi Differential Privacy 등의 포스트를 참고하시기 바랍니다.

Deep Learning Theory

파라미터 $\theta$에 대해, penalty를 나타내는 적절한 손실 함수 $\mathcal{L}$을 정의하면, empirical risk는 다음과 같이 정의할 수 있다. \(\mathcal{L}(\theta) = \frac{1}{N}\sum_{i}\mathcal{L}(\theta,x_{i})\)

일반적으로 최적화 문제 $\min_{\theta}\mathcal{L}(\theta)$ 를 풀기 위해서 Newton’s method나 L-BFGS와 같은 최적화 알고리즘을 사용한다. 그러나 Hessian matrix를 계산하는 것은 일반적인 딥러닝 세팅(large $N$)에서는 매우 비효율적이다. 따라서, 확률적 경사하강법 기반의 알고리즘을 사용한다.

즉, 전체 데이터의 랜덤한 부분집합인 배치^batch $B$를 만들고 다음과 같이 그래디언트를 계산한다.

\[g_{B} = \frac{1}{\vert B\vert} \sum_{x\in B} \nabla_{\theta}\mathcal{L}(\theta,x)\]

이는 전체 데이터에 대한 그래디언트 $\nabla_{\theta}\mathcal{L}(\theta)$의 추정값으로 간주되며, 업데이트 절차는 $-g_{B}$ 방향으로 주어진다.

\[\theta_{t+1} = \theta_{t} - \eta g_{B}\]

딥러닝에서 DP를 부여하기 위한 핵심 포인트는 SGD의 각 스텝에서 DP를 만족시키도록 하는 방법을 생각할 수 있다. 이를 위해 논문에서는 다음과 같은 알고리즘을 제시한다.

DP-SGD

DP-SGD 알고리즘은 다음과 같이 정의된다.

Noise clipping

Algorithm 1가 DP를 보장한다는 것을 확인하기 위해서 그래디언트의 유계성이 필요한데, 이를 위해 논문에서는 noise clipping을 사용한다. 이는 그래디언트의 L2 norm이 $C$를 넘지 않도록 하는 것인데, 다음과 같이 정의된다.

\[\bar g_{t}(x_i) = g_{t}(x_i) / \max\left(1, \frac{\left\Vert g_{t}(x_i)\right\Vert_{2}}{C}\right)\]

여기서 $C$는 clipping threshold를 나타낸다.

Moments Accountant

만약 다음과 같은 noise scale을 사용한다고 하자.

\[\sigma= \frac{1}{\epsilon} \sqrt{2\log \frac{1.25}{\delta}}\]

그러면 Algorithm 1의 각 스텝은 아래 strong composition theorem에 의해 각 배치 $L$에 대해 $(\epsilon,\delta)$-DP를 만족한다. 따라서 privacy amplification theorem에 의해 위 알고리즘은 전체 데이터셋에 대해 $(O(q\epsilon),q\delta)$-DP를 만족한다. 여기서 $q=L/N$은 배치의 샘플링 비율을 의미한다.

(Strong composition theorem)

\(\mathcal{M}_{1}\)이 \((\epsilon_{1}, \delta_{1})\)-DP 이고, \(\mathcal{M}_2\)가 \((\epsilon_{2},\delta_{2})\)-DP 라면 \(\mathcal{M}_{1}\circ \mathcal{M}_{2}\) 는 \((\epsilon_{1}+\epsilon_{2}, \delta_{1}+ \delta_{2})\)-DP 를 만족한다.

그러나 strong composition theorem의 bound는 tight하지 않다 (아래 그림 참고). 이 논문에서는 moments accountant라는 더 강력한 계산 방법을 제시한다. Moments accountant 정리를 이용하면, 적절한 노이즈와 clipping threshold를 선택하여 (이후 설명 참고) 위 알고리즘이 $(O(q \epsilon\sqrt{T}),\delta)$-DP 를 만족함을 보일 수 있다. 우선, 정리는 다음과 같이 주어진다.

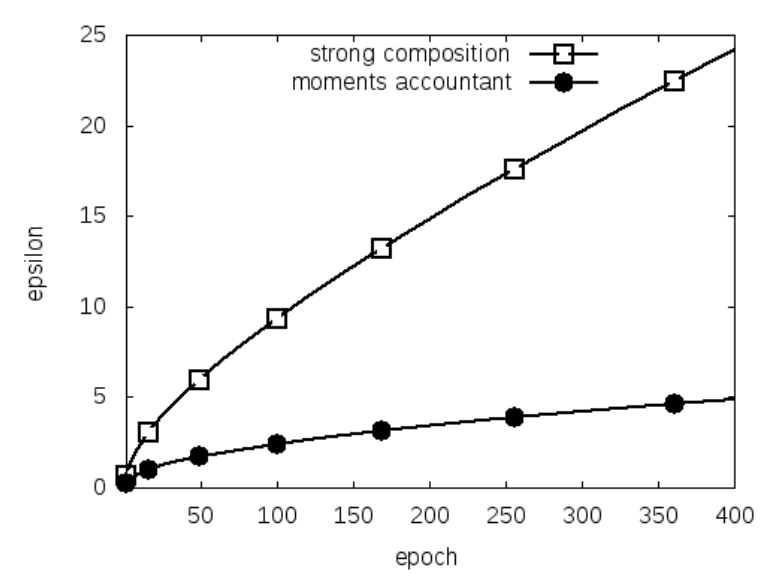Strong composition theorem와 moments accountant의 비교. Abadi et al. (2016)

Theorems

Theorem 1

상수 $c_{1},c_{2}$가 존재하여, 샘플링 비율 $q=L/N$과 스텝 수 $T$가 주어졌을 때, 임의의 $\epsilon<c_{1}q^{2}T$ 에 대해 위 Algorithm은 아래 조건 하에서 $(\epsilon,\delta)$-DP를 만족한다.

\[\sigma\ge c_{2} \frac{q\sqrt{T\log(1/\delta)}}{\epsilon}\]

만약 strong composition theorem을 사용한다면 $\sigma = \Omega(q\sqrt{T\log(1/\delta)\log(T/\delta)}/\epsilon)$이다. 예를 들어,

\[q=0.01, \sigma=4, \delta=10^{-5}, T=10000\]

일 때, moments accountant를 사용하면 $\epsilon\approx 1.26$이 되지만, strong composition theorem을 사용하면 $\epsilon\approx 9.34$가 된다. 결과적으로 moments accountant를 사용하면 더 작은 $\epsilon$을 얻을 수 있다.

이제 위 Theorem 1을 설명하기 위해 다음과 같은 정의들과 보조정리들을 이용한다.

Privacy Loss

우선 Privacy loss (혹은 privacy loss random variable)는 다음과 같이 randomized mechanism $\mathcal{M}$에 대해 정의되는 확률변수이다.

\[c(o;\mathcal{M},\text{aux},d,d') := \log \frac{\Pr (\mathcal{M}(\text{aux},d)=o)}{\Pr (\mathcal{M}(\text{aux},d')=o)}\]

여기서 $\mathrm{aux}$ 는 보조적인 입력값^{auxiliary input}, $d,d’$는 각각 데이터셋을 의미하며 $o$는 randomized mechanism $\mathcal{M}$의 출력값을 의미한다. ($o \in \mathrm{range}(\mathcal{M})$)

만일 위 randomized mechanism이 $\epsilon$-DP를 만족한다면, 이는 $\mathcal{M}$의 privacy loss random variable가 특정한 bound를 만족한다는 것과 동치임을 알 수 있다.

\[\begin{aligned} \Pr(\mathcal{M}(\text{aux},d) = o) &\le e^{\epsilon}\Pr(\mathcal{M}(\text{aux},d') = o)\\ \log \frac{\Pr(\mathcal{M}(\text{aux},d) = o)}{\Pr(\mathcal{M}(\text{aux},d') = o)} &\le \epsilon\\ c(o;\mathcal{M},\text{aux},d,d') &\le \epsilon \end{aligned}\]

Adaptive composition

일반적으로 머신러닝에서 우리가 mechanism이라고 할 수 있는 대부분의 알고리즘은 세부 메커니즘 여러 개를 순차적으로 적용하는 경우에 해당한다. 이를 adaptive composition이라고 하는데, 이전 단계 메커니즘의 출력이 다음 단계 메커니즘의 입력으로 작용하는 경우를 지칭한다. 이러한 경우, $k$번째 메커니즘의 auxiliary input $\text{aux}$ 는 이전 메커니즘들의 output $o_{1:k-1}$에 의존한다.

(Stochastic) Gradient descent의 경우, 각 스텝의 parameter $\theta_{t}$는 이전 스텝의 parameter $\theta_{t-1}$에 의존한다. 따라서 adaptive composition에 해당한다.

Log Moment Generating Function

확률변수 $X$의 cumulant generating function^CGF은 다음과 같이 moment generating function^MGF에 log를 취한 것으로 정의된다.

\[\alpha_X(\lambda) := \log \mathrm{E}\left[e^{\lambda X}\right]\]

이와 마찬가지로, privacy loss random variable $c(o;\mathcal{M},\text{aux},d,d’)$의 CGF를 다음과 같이 정의하자.

\[\alpha_\mathcal{M} (\lambda;\text{aux},d,d') := \log \mathrm{E}_{o\sim\mathcal{M}(\text{aux},d)}\left[\exp (\lambda c(o;\mathcal{M},\text{aux},d,d'))\right]\]

앞서 privacy loss random variable의 bound가 DP와 동치라고 하였기 때문에, CGF의 bound를 다루는 것 역시 유용하다. 따라서 다음과 같이 CGF의 upper bound를 정의하기로 하자.

\[\alpha_\mathcal{M} (\lambda) := \max_{\text{aux},d,d'}\log \mathrm{E}_{o\sim\mathcal{M}(\text{aux},d)}\left[\exp (\lambda c(o;\mathcal{M},\text{aux},d,d'))\right]\]

여기서 최댓값 연산은 모든 이웃 데이터셋 $d,d’$과 모든 보조입력에 대해 이루어진다. 또한, 여기서 사용되는 $\lambda$는 MGF, CGF를 정의할 때 사용되는 변수이다. (MGF $\mathrm{E}e^{tX}$ 에서의 $t$와 동일한 역할)

Theorem 2

위와 같이 정의한 CGF의 upper bound $\alpha_\mathcal{M}(\lambda)$ 에 대해 다음 두 가지 성질이 성립한다.

Composability

메커니즘 $\mathcal{M}$ 이 sequential하게 정의되며, \(\mathcal{M}_{1},\cdots,\mathcal{M}_{k}\)로 구성된다고 하자. 이때, 각 element mechanism은 \(\mathcal{M}_{i}:\prod_{j=1}^{i-1} \mathcal{R}_{j}\times \mathcal{D}\to \mathcal{R}_{i}\) 으로 정의된다. 그러면 $\forall \lambda$ 에 대해 다음이 성립한다.

\[\alpha_\mathcal{M}(\lambda) \le \sum_{i=1}^{k}\alpha_\mathcal{M_{i}}(\lambda).\]

Proof.

\(\mathcal{M}_{1:i}= (\mathcal{M}_{1},\cdots,\mathcal{M}_{i})\) 라고 나타내자. 또한, $i$번째 단계에서의 output을 $o_i$라고 하고, \(o_{1:i}=(o_{1},\cdots,o_{i})\) 라고 나타내자.

임의의 이웃하는 데이터셋 $d,d’$에 대해 다음이 성립한다.

\[\begin{aligned} c(&o_{1:k};\mathcal{M}, o_{1:k-1},d,d')\\ &= \log \frac{\Pr(\mathcal{M}_{1:k}(d; o_{1:k-1})=o_{1:k})}{\Pr(\mathcal{M}_{1:k}(d'; o_{1:k-1})=o_{1:k})}\\ &= \log \prod_{i=1}^{k}\frac{\Pr(\mathcal{M}_{i}(d)=o_{i}|\mathcal{M}_{1:i-1}(d)=o_{1:i-1})}{\Pr(\mathcal{M}_{i}(d')=o_{i}|\mathcal{M}_{1:i-1}(d')=o_{1:i-1})}\\ &= \sum_{i=1}^{k}c(o_{i};\mathcal{M}_{i},o_{1:i-1},d,d'). \end{aligned}\]

즉, sequential한 메커니즘 $\mathcal{M}$의 privacy loss random variable은 각 단계의 privacy loss random variable의 합으로 표현할 수 있다.

여기서 두번째 등호는 sequential한 메커니즘의 정의에 의해 성립한다. (Markov property와 유사)

이로부터 다음이 성립한다.

\[\begin{aligned} &\mathrm{E}_{o'_{1:k}\sim \mathcal{M}_{1:k}(d)}\left[\exp(\lambda c(o'_{1:k};\mathcal{M}_{1:k},d,d')) \mid \forall i<k: o'_i = o_i\right] \\ &= \mathrm{E}_{o'_{1:k}\sim \mathcal{M}_{1:k}(d)}\left[\exp(\lambda \sum_{i=1}^{k}c(o'_{i};\mathcal{M}_{i},o_{1:i-1},d,d'))\right]\\ &= \mathrm{E}_{o'_{1:k}\sim \mathcal{M}_{1:k}(d)}\left[\prod_{i=1}^{k}\exp(\lambda c(o'_{i};\mathcal{M}_{i},o_{1:i-1},d,d'))\right] \end{aligned}\]

이때, 각 노이즈가 독립이므로

\[\begin{aligned} &\mathrm{E}_{o'_{1:k}\sim \mathcal{M}_{1:k}(d)}\left[\prod_{i=1}^{k}\exp(\lambda c(o'_{i};\mathcal{M}_{i},o_{1:i-1},d,d'))\right]\\ &= \prod_{i=1}^{k}\mathrm{E}_{o'_{i}\sim \mathcal{M}_{i}(d)}\left[\exp(\lambda c(o'_{i};\mathcal{M}_{i},o_{1:i-1},d,d'))\right]\\ &= \exp\left(\sum_{i=1}^{k}\alpha_{\mathcal{M}_{i}}(\lambda)\right). \end{aligned}\]

이로부터 $\alpha_{\mathcal{M}}(\lambda)\le \sum_{i=1}^{k}\alpha_{\mathcal{M}_{i}}(\lambda)$임을 알 수 있다.

Tail Bound

임의의 $\epsilon>0$에 대해, 메커니즘 $\mathcal{M}$이 다음을 만족하면 $(\epsilon,\delta)$-DP 메커니즘이다.

\[\delta= \min_\lambda\exp(\alpha_\mathcal{M}(\lambda)-\lambda \epsilon).\]

Proof.

Markov inequality에 의해 다음이 성립한다.

\[\begin{align} \Pr_{o\sim \mathcal{M}(d)} (c(o) \geq \epsilon) &= \Pr_{o\sim \mathcal{M}(d)} (\exp (\lambda c(o)) \geq \exp(\lambda \epsilon))\\ &\le \frac{\mathrm{E}_{o}\exp(\lambda c(o))}{\exp(\lambda \epsilon)}\\ &\le \exp (\alpha-\lambda \epsilon). \tag{1} \end{align}\]

$B = \lbrace o : c(o) \ge \epsilon\rbrace$ 를 정의하면 임의의 $S$에 대해 다음 부등식이 성립한다.

\[\begin{align} \Pr(\mathcal{M}(d)\in S) &= \Pr (\mathcal{M}(d)\in S\cap B^{c}) + \Pr (\mathcal{M}(d)\in S\cap B)\\ &\le \exp(\epsilon)\Pr (\mathcal{M}(d') \in S) +\exp(\alpha-\lambda \epsilon) \end{align}\]

두번째 항에 대해서는 부등식 $(1)$을 사용하면 된다.

Lemma. Composability of Gaussian mechanism

이제, 정리 1을 증명하기 위해 다음 보조 정리를 이용한다.

함수 $f:D\to \mathbb{R}^{p}$ 가 $\left\Vert f(\cdot)\right\Vert_{2}\le 1$ 을 만족한다고 하자. $\sigma \ge 1$ 이고 $J$가 $[n]=\lbrace 1,\ldots,n\rbrace$ 으로부터의 랜덤 샘플이라고 하자. 이때 각 원소는 확률 $q < \frac{1}{16\sigma}$ 로 독립적으로 선택된다고 하자. 그러면 임의의 양의 정수 $\lambda\le \sigma^{2}\log \frac{1}{q\sigma}$ 에 대해 다음 Gaussian mechanism

\[\mathcal{M}(d) = \sum_{i\in J}f(d_{i}) + \mathcal{N}(0,\sigma^{2}\mathbf{I})\]

의 CGF는 다음을 만족한다.

\[\alpha_\mathcal{M}(\lambda) \le \frac{q^{2}\lambda(\lambda+1)}{(1-q)\sigma^{2}}+O(q^{3}\lambda^{3}/\sigma^{3}).\]

Proof.

일반성을 잃지 않고(WLOG), $d=d’\cup \lbrace d_n\rbrace$, \(f(d_n)=\mathbf{e}_1\), \(\sum_{i\in J\backslash \{n\}}f(d_{i})=\mathbf{0}\) 라고 두자. 그러면 $\mathcal{M}(d)$와 $\mathcal{M}(d’)$는 첫 번째 원소를 제외하고 동일한 분포 (Gaussian)를 갖는다.

$\mu_0, \mu_1$를 각각 $N(0,\sigma^{2})$, $N(1,\sigma^{2})$의 확률밀도함수로 두자. 그러면 $q$의 확률로 $d_n$이 추가되므로, 다음 관계가 성립한다.

\[\begin{aligned} \mathcal{M}(d') &\sim \mu_0\\ \mathcal{M}(d) &\sim\mu \triangleq (1-q)\mu_0 + q\mu_1 \end{aligned}\]

이때 다음을 보이면 된다.

\[\begin{aligned} \mathrm{E}_{z\sim \mu}\left[\left(\frac{\mu(z)}{\mu_0(z)}\right)^{\lambda}\right] &\le \alpha \\ \mathrm{E}_{z\sim \mu_0}\left[\left(\frac{\mu_0(z)}{\mu(z)}\right)^{\lambda}\right] &\le \alpha \end{aligned}\]

두 분포 $\nu_0, \nu_1$에 대해 다음 관계가 성립한다.

\[\mathrm{E}_{\nu_0}\left(\frac{\nu_0}{\nu_1}\right)^\lambda = \mathrm{E}_{\nu_1}\left(\frac{\nu_0}{\nu_1}\right)^{\lambda+1}\]

이항전개를 이용하면 다음이 성립한다.

\[\begin{aligned} \mathrm{E}_{\nu_1}[(\nu_0/\nu_1)^{\lambda+1}] &= \mathrm{E}_{\nu_1}[(1 + (\nu_0 - \nu_1)/\nu_1)^{\lambda+1}]\\ &= \sum_{i=0}^{\lambda+1}\binom{\lambda+1}{i}\mathrm{E}_{\nu_1}[((\nu_0 - \nu_1)/\nu_1)^{i}] \end{aligned}\]

첫번째 항은 $1$ 이고, 두번째 항은

\[\begin{aligned} \mathrm{E}_{\nu_1}\left[\frac{\nu_0-\nu_1}{\nu_1}\right] &= \int \nu_1 \frac{\nu_0-\nu_1}{\nu_1}d\nu_1\\ &= \int \nu_0 - \nu_1 d\mu \\ &= \int \nu_0 d\mu - \int \nu_1 d\mu\\ &= 0 \end{aligned}\]

이므로, 위 Lemma를 증명하기 위해서는 세번째 항이 $q^{2}\lambda(\lambda+1)/(1-q)\sigma^{2}$ 로 bound되는 것을 보이면 된다.

$\nu_0 = \mu_0, \nu_1 = \mu$ 인 케이스에 대해 이를 보이도록 하자. (반대의 경우도 비슷하게 증명할 수 있다.)

우선, $\mu = (1-q)\mu_0 + q\mu_1$ 이므로 다음이 성립한다.

\[\begin{aligned} \mathrm{E}_{z\sim\mu}\left[\left(\frac{\mu_0(z)-\mu(z)}{\mu(z)}\right)^2\right] &= q^2 \mathrm{E}_{z\sim\mu_1}\left[\left(\frac{\mu_0(z)-\mu_1(z)}{\mu(z)}\right)^2\right]\\ &= q^2 \int \frac{(\mu_0(z)-\mu_1(z))^2}{\mu(z)}dz\\ &\leq \frac{q^2}{1-q} \int \frac{(\mu_0(z)-\mu_1(z))^2}{\mu_0(z)}dz\\ &= \frac{q^2}{1-q} \mathrm{E}_{z\sim\mu_0}\left[\left(\frac{\mu_0(z)-\mu_1(z)}{\mu_0(z)}\right)^2\right] \end{aligned}\]

여기서 부등식은 $\mu \ge (1-q)\mu_0$ 로부터 성립한다. 또한, 임의의 $a\in \mathbb{R}$에 대해

\[\mathrm{E}_{z\sim \mu_0} \exp\left(\frac{2az}{2\sigma^2}\right) = \exp\left(\frac{a^2}{2\sigma^2}\right)\]

이므로 이를 이용하면,

\[\begin{aligned} \mathrm{E}_{z\sim \mu_0}\left[\left(\frac{\mu_0(z)-\mu_1(z)}{\mu_0(z)}\right)^2\right] &= \mathrm{E}_{z\sim \mu_0}\left[\left(1- \exp\left(\frac{2z-1}{2\sigma^2}\right)\right)^2\right]\\ &= 1- 2\mathrm{E}_{z\sim \mu_0}\left[\exp\left(\frac{2z-1}{2\sigma^2}\right)\right] + \mathrm{E}_{z\sim \mu_0}\left[\exp\left(\frac{4z-2}{2\sigma^2}\right)\right]\\ &= 1- 2\exp\left(\frac{1}{2\sigma^2}\right)\exp\left(-\frac{1}{2\sigma^2}\right) \\ &+ \exp\left(\frac{4}{2\sigma^2}\right)\exp\left(-\frac{2}{2\sigma^2}\right)\\ &= \exp\left(\frac{1}{\sigma^2}\right) - 1 \end{aligned}\]

이 성립한다. 따라서, 앞선 이항전개 결과의 세번째 항은

\[\binom{\lambda+1}{2} \mathrm{E}_{z\sim\mu}\left[\left(\frac{\mu_0(z)-\mu_1(z)}{\mu(z)}\right)^2\right] \le \frac{q^2\lambda(\lambda+1)}{(1-q)\sigma^2}\]

으로 bound된다.

나머지 항들은 다음과 같은 방법으로 bound할 수 있다.

우선, $z$의 범위에 따라 다음 관계들이 성립한다.

\[|\mu_0(z)-\mu_1(z)| \le \begin{cases} -(z-1)\mu_0(z)/\sigma^2, & z \le 0 \\ z\mu_1(z)/\sigma^2, & z \ge 1 \\ \mu_0(z)/\sigma^2, & 0 \le z \le 1 \end{cases}\]

이에 따라 이항전개 결과에서의 $t$번째 항에서의 기댓값 부분을 다음과 같이 분해하자.

\[\begin{aligned} &\mathrm{E}_{\mu}\left[\left(\frac{\mu_0(z)-\mu(z)}{\mu(z)}\right)^t\right] \\ &\le \int_{-\infty}^0 \mu(z) \left|\left(\frac{\mu_0(z)-\mu(z)}{\mu(z)}\right)^t\right| dz \\ &+ \int_0^1 \mu(z) \left|\left(\frac{\mu_0(z)-\mu(z)}{\mu(z)}\right)^t\right| dz \\ &+ \int_1^\infty \mu(z) \left|\left(\frac{\mu_0(z)-\mu(z)}{\mu(z)}\right)^t\right| dz \end{aligned}\]

이때 다음이 성립하므로

\[\begin{gathered} \mu_0 - \mu = q(\mu_0 - \mu_1) \\ \mu \ge (1-q)\mu_0\\ \mathrm{E}_{\mu_0}|z|^t \le \sigma^t (t-1)!! \end{gathered}\]

이항계수와 함께 각 항을 bound하면 다음이 성립한다.

\[\begin{aligned} \frac{q^t}{(1-q)^{t-1}\sigma^{2t}}&\int_{-\infty}^0 \mu_0(z) |z-1|^t dz \\ &\le \frac{(2q)^t(t-1)!!}{2(1-q)^{t-1}\sigma^{t}} \\ \frac{q^t}{(1-q)^t}&\int_0^1 \mu(z) \left|\left(\frac{\mu_0(z)-\mu_1(z)}{\mu(z)}\right)^t\right| dz \\ &\le \frac{q^t}{(1-q)^t}\int_0^1 \mu(z) \frac{1}{\sigma^{2t}}dz\\ & \le \frac{q^t}{(1-q)^t\sigma^{2t}}\\ \frac{q^t}{(1-q)^{t-1}\sigma^{2t}}&\int_1^\infty \mu_0(z) \left(\frac{z\mu_1(z)}{\mu_0(z)}\right)^t dz \\ &\le \frac{q^t}{(1-q)^{t-1}\sigma^{2t}}\int_1^\infty \mu_0(z)\exp((2tz-t)/2\sigma^2)z^t dz\\ &\le \frac{q^t \exp((t^2-t)/2\sigma^2)}{(1-q)^{t-1}\sigma^{2t}}\int_0^\infty \mu_0(z-t)z^t dz\\ &\le \frac{(2q)^t\exp((t^2-t)/2\sigma^2)(\sigma^t(t-1)!!+t^t)}{2(1-q)^{t-1}\sigma^{2t}} \end{aligned}\]

이로부터 $t>3$인 경우에는 $O(q^3\lambda^3/\sigma^3)$으로 bound됨을 알 수 있다.

Implication

1. 정리 2의 composability로부터 만일 우리가 다루는 randomized mechanism $\mathcal{M}$이 adaptive mechanism들의 함수열로 주어진다면 (\(\mathcal{M}_{i} : i=1,\cdots,k\)), 실제 알고리즘에서는 $i$번째 단계마다의 bound \(\alpha_{\mathcal{M}_{i}}(\lambda)\) 를 계산하고 이들의 합을 취하면 전체 알고리즘 $\mathcal{M}$의 moment bound $\alpha_\mathcal{M}(\lambda)$를 얻을 수 있다.

2. 정리 2의 Tail bound로부터 앞서 구한 $\alpha_\mathcal{M}(\lambda)$를 이용해 $\delta$ 값을 계산할 수 있게 된다. (혹은 $\delta$를 미리 상정한 상황에서는 $\epsilon$ 값을 계산할 수 있다.)

DP to Moments bounds

Randomized mechanism의 Differential privacy와 moment bound는 다음과 같이 변환이 가능하다.

$\mathcal{M}$이 $\epsilon$-DP 메커니즘이라면, 임의의 $\lambda>0$ 에 대해 $\mathcal{M}$의 CGF는 다음을 만족한다.

\[\alpha_\mathcal{M}(\lambda)\le \lambda \epsilon(e^{\epsilon}-1)+\lambda^{2}\epsilon^{2}e^{2\epsilon}/2.\]

Proof

$Z$가 privacy loss random variable $c(\mathcal{M}(d))$ 이라고 하자. 그러면 $\epsilon$-DP 메커니즘 $\mathcal{M}$은 다음을 만족한다.

\[\begin{align} \mathrm{E}[Z] &\le \epsilon(\exp (\epsilon)-1)\\ \left\vert Z\right\vert &\le \epsilon,\text{ so that } \left\vert Z-\mu\right\vert \leq \epsilon\exp (\epsilon) \end{align}\]

이로부터 위 결과를 얻을 수 있다.

Implementation

DP-SGD를 활용한 python 구현 예시는 다음 게시글을 참고하면 된다.

Differentially Private Variational Inference

References

• Abadi, M., Chu, A., Goodfellow, I., McMahan, H. B., Mironov, I., Talwar, K., & Zhang, L. (2016). Deep Learning with Differential Privacy. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, 308–318. https://doi.org/10.1145/2976749.2978318
• Dwork, C., Rothblum, G. N., & Vadhan, S. (2010). Boosting and Differential Privacy. 2010 IEEE 51st Annual Symposium on Foundations of Computer Science, 51–60. https://doi.org/10.1109/FOCS.2010.12