Diffusion Models
Diffusion Models
디퓨전 모델Diffusion Models은 최근 이미지 생성 분야에서 가장 널리 사용되고 있는 딥러닝 아키텍쳐 중 하나이고, VAE, Normalizing Flow 등의 모델과 유사하다. 기본적인 아이디어는 노이즈로부터 구조화된 데이터(e.g. 이미지)를 찾는 것은 어렵지만, 구조화된 데이터를 노이즈로 변환하는 것은 비교적 간단하다는 것이다.이러한 과정을 diffusion process라고 하며, normalizing flow와 유사하게 주어진 데이터에 sequential한 변수변환을 주어 데이터 $\mathbf{x}_{0}$를 \(\mathbf{x}_{T}\sim N(\mathbf{0},\mathbf{I})\)으로 변환한다. 이후, VAE와 유사하게 노이즈로부터 구조화된 데이터를 복원하게 된다.
Denoising diffusion probabilistic models (DDPM)
2015년에 제안된 denoising diffusion probabilistic models, 줄여서 DDPM이라고 부르는 모델은 디퓨전 모델의 근간이 된다 (Ho et al., 2020). 앞서 언급한 것과 같이, 주어진 input data $\mathbf{x}_{0}$를 latent states \(\mathbf{x}_{1},\cdots,\mathbf{x}_{T}\)로 변환시키며 최종적으로는 노이즈 형태로 변환하는 것이 목적이다. VAE와 마찬가지로 이러한 구조를 encoder로 정의하며, 아래 그림의 \(q(\mathbf{x}_{t}\vert \mathbf{x}_{t-1})\)을 의미한다.
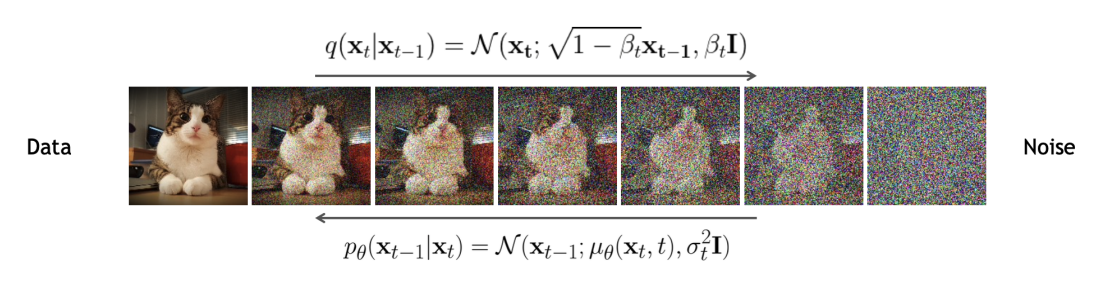 DDPM의 구조 (Murphy, 2023)
DDPM의 구조 (Murphy, 2023)
다만, normalizing flow는 이러한 변환 $q$들에 대해 각각의 역변환이 존재해야 하지만(invertible), 디퓨전 모델에서는 그러한 제약조건이 존재하지 않는다. 또한, 인코더의 각 변환 $q$를 간단한 linear Gaussian model으로 구성하는데 DDPM에서는 이러한 인코더를 학습시키지 않는다는 특징이 있다.
노이즈를 기존 구조화된 데이터로 복원시키는 과정을 decoder로 정의하며, 이는 VAE에서의 경우와 마찬가지로 각 변환에 파라미터를 주어, 이들을 모델 훈련 과정에서 학습시키게 된다.
Encoder
Encoder process의 각 과정은 Markov property를 갖는 simple Linear Gaussian으로 가정한다. 즉, 다음과 같이 주어진다.
\[q(\mathbf{x}_{t}\mid \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_{t}\vert \sqrt{1-\beta_{t}}\mathbf{x}_{t-1},\beta_{t}\mathbf{I})\]이때 $\beta$값들은 noise schedule에 따라 결정된다. 위 가정으로부터 잠재변수들에 대한 결합확률밀도는 다음과 같이 계산된다.
\[q(\mathbf{x}_{1:T}\mid \mathbf{x}_{0}) = \prod_{t=1}^{T}q(\mathbf{x}_{t}\mid \mathbf{x}_{t-1})\]이는 Markov chain이 되므로 marginal distribution을 다음과 같이 구할 수 있다.
\[\begin{align} q(\mathbf{x}_{t}\mid \mathbf{x}_{0}) &= \mathcal{N}(\mathbf{x}_{t}\mid \sqrt{\bar \alpha_{t}}\mathbf{x}_{0},(1-\bar \alpha_{t})\mathbf{I})\\ \alpha_{t}&=1-\beta_{t}\\ \bar \alpha_{t} &= \prod_{s=1}^{t}\alpha_{s} \end{align}\]최종적으로 $T$ step에서는 $\mathcal{N}(\mathbf{0},\mathbf{I})$를 도출해야 하므로, $\bar \alpha_{T}\approx 0$이 되도록 하는 것이 noise schedule이다. 또한, 주어진 input data의 분포로부터 unconditional marginal
\[q(\mathbf{x}_{t}) = \int q_{0}(\mathbf{x}_{0})q(\mathbf{x}_{t}\mid \mathbf{x}_{0})d \mathbf{x}_{0}\]을 계산할 수 있다. 주목할 것은, $t$가 증가함에 따라 marginal이 점차 간단해진다는 것이다.
Decoder
Decoder는 encoder process의 역변환으로 정의할 수 있다. 만약 input data $\mathbf{x}_{0}$이 주어지면 이는 다음과 같다.
\[\begin{align} q(\mathbf{x}_{t-1}\mid \mathbf{x}_{t},\mathbf{x}_{0}) &= \mathcal{N}(\mathbf{x}_{t-1}\mid \tilde \mu_{t}(\mathbf{x}_{t},\mathbf{x}_{0}),\tilde \beta_{t}\mathbf{I})\\ \tilde \mu_{t}(\mathbf{x}_{t},\mathbf{x}_{0}) &= \frac{\sqrt{\bar \alpha_{t-1}}\beta_{t}}{1-\bar \alpha_{t}}\mathbf{x}_{0}+ \frac{\sqrt{\alpha_{t}}(1-\bar \alpha_{t-1})}{1-\bar \alpha_{t}}\mathbf{x}_{t}\\ \tilde \beta_{t}&= \frac{1-\bar \alpha_{t-1}}{1-\bar \alpha_{t}}\beta_{t} \end{align}\]다만, 학습 과정이 아닌 데이터 생성 과정에서는 \(\mathbf{x}_{0}\)에 대한 정보가 없으므로, 이 경우에는 \(\mathbf{x}_{0}\)을 평균적으로 잘 근사하는 approximator $p$를 학습시킨다.
\[p_{\theta}(\mathbf{x}_{t-1}\mid \mathbf{x}_{t}) = \mathcal{N}(\mathbf{x}_{t-1}\mid \mu_\theta(\mathbf{x}_{t},t),\Sigma_\theta(\mathbf{x}_{t},t))\]Model Fitting
DDPM은 VAE와 유사하게, ELBOevidence lower bound를 최대화하는 방향으로 모델 학습을 진행시킨다. 이때, evidence는 decoder에서의 input data의 marginial probability $\log p_\theta(\mathbf{x}_{0})$으로 주어진다. 이는 다음과 같이 나타낼 수 있다.
\[\log p_\theta(\mathbf{x}_{0:T}) = \log p(\mathbf{x}_{T}) + \sum_{t=1}^{T}p_\theta(\mathbf{x}_{t-1}\mid \mathbf{x}_{t})\]따라서, ELBO는 다음과 같이 주어진다.
\[\begin{align} \log p_\theta(\mathbf{x}_{0}) &= \log \left(\int p_\theta(\mathbf{x}_{0:T}) d \mathbf{x}_{1:T}\right)\\ &= \log \left(\int q(\mathbf{x}_{1:T}\mid \mathbf{x}_{0})\frac{p_{\theta}(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}\mid \mathbf{x}_{0})} d \mathbf{x}_{1:T}\right)\\ &= \int \left(\log p(\mathbf{x}_{T}) + \sum_{t=1}^{T }\log \frac{p_{\theta}(\mathbf{x}_{t-1}\mid \mathbf{x}_{t})}{q(\mathbf{x}_{t}\mid \mathbf{x}_{t-1})}\right)q(\mathbf{x}_{1:T}\mid \mathbf{x}_{0})d \mathbf{x}_{1:T}\\ &= \mathrm{E}_{q}\left[\log p(\mathbf{x}_{T}) + \sum_{t=1}^{T}\log \frac{p_{\theta}(\mathbf{x}_{t-1}\mid \mathbf{x}_{t})}{q(\mathbf{x}_{t}\mid \mathbf{x}_{t-1})}\right]\overset{\triangle}{=}\mathrm{ELBO}(\mathbf{x}_{0}) \end{align}\]이때, Markov property \(q(\mathbf{x}_{t}\mid \mathbf{x}_{t-1})=q(\mathbf{x}_{t}\mid \mathbf{x}_{t-1},\mathbf{x}_{0})\)으로부터
\[q(\mathbf{x}_{t}\mid \mathbf{x}_{t-1},\mathbf{x}_{0}) = \frac{q(\mathbf{x}_{t-1}\mid \mathbf{x}_{t},\mathbf{x}_{0})q(\mathbf{x}_{t}\mid \mathbf{x}_{0})}{q(\mathbf{x}_{t-1}\mid \mathbf{x}_{0})}\]이 성립한다. 이를 이용하여 ELBO를 정리하면, 다음과 같다.
\[\begin{align} \mathcal{L}(\mathbf{x}_{0})=-\mathrm{ELBO}(\mathbf{x}_{0})&= -\mathrm{E}_{q(\mathbf{x}_{1:T}\mid \mathbf{x}_{0})}\left[\log \frac{p(\mathbf{x}_{T})}{q(\mathbf{x}_{T}\mid \mathbf{x}_{0})}+ \sum_{t=2}^{T}\log \frac{p_{\theta}(\mathbf{x}_{t-1}\mid \mathbf{x}_{t})}{q(\mathbf{x}_{t-1}\mid \mathbf{x}_{t},\mathbf{x}_{0})}+\log p_\theta(\mathbf{x}_{0}\mid \mathbf{x}_{1})\right]\\ &= D_{KL}\left(q(\mathbf{x}_{T}\mid \mathbf{x}_{0})\Vert p(\mathbf{x}_{T})\right)\\ &+ \sum_{t=2}^{T}\mathrm{E}_{q(\mathbf{x}_{t}\mid \mathbf{x}_{0})}D_{KL} \left(q(\mathbf{x}_{t-1}\mid \mathbf{x}_{t},\mathbf{x}_{0}) \Vert p_\theta(\mathbf{x}_{t-1}\mid \mathbf{x}_{t})\right) - \mathrm{E}_{q(\mathbf{x}_{1}\mid \mathbf{x}_{0})}\log p_\theta(\mathbf{x}_{0}\mid \mathbf{x}_{1}) \end{align}\]Simplified Loss
ELBO의 마지막 식에서 다음 KL term에 주목해보자.
\[L_{t-1} \overset{\triangle}{=} D_{KL} \left(q(\mathbf{x}_{t-1}\mid \mathbf{x}_{t},\mathbf{x}_{0}) \Vert p_\theta(\mathbf{x}_{t-1}\mid \mathbf{x}_{t})\right)\]이는 Input \(\mathbf{x}_{0}\)가 주어질 때 디코더 과정의 분포와 그렇지 않은 경우의 분포 간 KL divergence를 나타낸 것이다. 디코더에서, \(\mathbf{x}_{0}\)가 주어진 경우 \(\mathbf{x}_{t-1}\)의 평균은
\[\tilde \mu_{t}(\mathbf{x}_{t},\mathbf{x}_{0}) = \frac{\sqrt{\bar \alpha_{t-1}}\beta_{t}}{1-\bar \alpha_{t}}\mathbf{x}_{0}+ \frac{\sqrt{\alpha_{t}}(1-\bar \alpha_{t-1})}{1-\bar \alpha_{t}}\mathbf{x}_{t}\]로 나타냈었다. 이때, \(\mathbf{x}_{t}=\sqrt{\bar \alpha_{t}}\mathbf{x}_{0}+\sqrt{(1-\bar \alpha_{t})}\epsilon, \epsilon\sim N(0,I)\) 으로 나타낼 수 있으므로 위 식은 다음과 같이 변환가능하다.
\[\tilde \mu_{t}(\mathbf{x}_{t},\mathbf{x}_{0}) = \frac{1}{\sqrt{\alpha_{t}}}\left(\mathbf{x}_{t}- \frac{\beta_{t}}{\sqrt{1-\bar \alpha_{t}}}\epsilon\right)\]반면, \(\mathbf{x}_{0}\)가 주어지지 않을 때 디코더 과정의 분포를 생각해보자. \(\mu_{\theta}(x_{t},t)\)로 parameterized 하였는데, 노이즈 분포의 모수를 학습하는 방향으로 설정하여 다음과 같이 나타낼 수 있다.
\[\mu_{\theta}(\mathbf{x}_{t},\mathbf{x}_{0}) = \frac{1}{\sqrt{\alpha_{t}}}\left(\mathbf{x}_{t}- \frac{\beta_{t}}{\sqrt{1-\bar \alpha_{t}}}\epsilon_{\theta}(x_{t},t )\right)\]이를 이용하면, $L_{t-1}$ 항을 아래와 같이 나타낼 수 있다.
\[\begin{align} L_{t-1}&= \mathrm{E}_{\mathbf{x}_{0}\sim q_{0}}\left[\frac{\beta_{t}^{2}}{2\sigma_{t}^{2}\alpha_{t}(1-\bar \alpha_{t})}\left\Vert\epsilon-\epsilon_{\theta}\left(\sqrt{\bar \alpha_{t}}\mathbf{x}_{0}+\sqrt{1-\bar \alpha_{t}}\epsilon,t\right)\right\Vert^{2}\right]\\ &= \mathrm{E}_{\mathbf{x}_{0}\sim q_{0}}\left[\lambda_{t}\left\Vert\epsilon-\epsilon_{\theta}\left(\sqrt{\bar \alpha_{t}}\mathbf{x}_{0}+\sqrt{1-\bar \alpha_{t}}\epsilon,t\right)\right\Vert^{2}\right] \end{align}\]여기서 $\lambda_{t}$ 부분이 목적함수 $\mathcal{L}$을 최적화하는 문제가 최대가능도 추정의 방향으로 학습이 진행되도록 하는 역할을 한다. 다만, 실험적으로 $\lambda_{t}=1$ 로 세팅하는 것이 모델의 샘플 생성 과정에서 더 나은 결과를 갖는다는 것이 알려져 있다고 한다. 이러한 세팅에서의 loss를 simplified loss라고 한다.
Noise Scheduling
이번에는 앞서 언급한 noise schedule 방법에 대해 살펴보고자 한다. Noise scheduling은 인코더 부분에서 이루어지며, 이 과정으로 ELBO를 최대화한다. 이러한 접근법을 Variational Diffusion Model 이라고도 한다 (Kingma et al., 2023). 우선, 인코더의 marginal distribution을 다음과 같이 나타내도록 하자.
\[q(\mathbf{x}_{t}\mid \mathbf{x}_{0}) = \mathcal{N}(\mathbf{x}_{t}\mid \hat \alpha_{t}\mathbf{x}_{0},\hat \sigma_{t}^{2}\mathbf{I})\tag{1}\]여기서 모수 $\hat \alpha_{t},\hat \sigma_{t}^{2}$를 각각 학습하기 보다는 이들의 비율인 signal noise ratio(SNR) 를 학습한다.
\[R(t) = \frac{\hat \alpha^{2}_{t}}{\hat \sigma^{2}_{t}}\]$t$가 증가할수록 \(q(\mathbf{x}_{t}\mid \mathbf{x}_{0})\)이 \(N(0,\mathbf{I})\)에 수렴하므로 $R(t)$는 $t$에 대한 단조감소함수임을 확인할 수 있다. 일반적으로 monotonic neural network $\gamma_{\phi}$를 이용하여 $R(t)=\exp(-\gamma_{\phi}(t))$ 로 나타낸다.
Negative ELBO $\mathcal{L}$을 다음과 같이 나타내자.
\[\mathcal{L}(\mathbf{x}_{0}) = \mathrm{KL}\left(q(\left(\mathbf{x}_{T}\mid \mathbf{x}_{0}\right)\Vert p(\mathbf{x}_{T})\right) + \mathrm{E}_{q(\mathbf{x}_{1}\mid \mathbf{x}_{0})}[-\log p_{\theta}(\mathbf{x}_{0}\mid \mathbf{x}_{1}) + \mathcal{L}_{D}(\mathbf{x}_{0})\]Parametrization $(1)$로부터 Diffusion loss $\mathcal{L}_{D}$는 다음과 같이 주어진다.
\[\mathcal{L}_{D}(\mathbf{x}_{0}) = \frac{1}{2}\mathrm{E}\left[\int_{0}^{1}R'(t)\Vert \mathbf{x}_{0}-\hat{\mathbf{x}}_{\theta}(\mathbf{z}_{t},t)\Vert^{2}_{2}\right]dt\]여기서 \(\mathbf{z}_{t}=\alpha_{t}\mathbf{x}_{0}+\sigma_{t}\epsilon\)이고 \(\epsilon\sim \mathcal{N}(\mathbf{0},\mathbf{I})\) 이다. 그런데, SNR 함수 $R$은 역함수가 존재하기 때문에, \(\tilde{\mathbf{x}}_{\theta}(\mathbf{z},t)=\hat{\mathbf{x}}_{\theta}(\mathbf{z}_{t},R^{-1}(t))\) 가 성립하고 diffusion loss는 다음과 같이 변환가능하다.
\[\mathcal{L}_{D}(\mathbf{x}_{0}) = \frac{1}{2}\mathrm{E}\left[\int_{R(0)}^{R(1)}\left\Vert \mathbf{x}_{0}-\tilde{\mathbf{x}}_{\theta}(\mathbf{z}_{v},v)\right\Vert_{2}^{2}dv\right]\]위 적분은 timestep $t\in[T]$ 를 샘플링하여 근사할 수 있다. 다만, 무작위로 독립적인 timestep들을 추출하는 것 대신에 low-discrepancy sampler을 이용할 수 있는데, 이는 $u_{0}\sim\mathrm{Unif}(0,1)$ 을 샘플링하여 $i$번째 timestep으로 $t^{i}=\mod (u_{0} + \dfrac{i}{k}, 1)$ 을 사용한다.
References
- Ho, J., Jain, A., & Abbeel, P. (2020). Denoising Diffusion Probabilistic Models (arXiv:2006.11239). arXiv. http://arxiv.org/abs/2006.11239
- Murphy, K. P. (2023). Probabilistic machine learning: Advanced topics. The MIT Press.
- Kingma, D. P., Salimans, T., Poole, B., & Ho, J. (2023). Variational Diffusion Models (arXiv:2107.00630). arXiv. https://doi.org/10.48550/arXiv.2107.00630
Leave a comment