이번 글에서는 Point Process 데이터를 분석하는 방법에 대해 Pysal 패키지와 예제 데이터를 바탕으로 살펴보도록 하겠다. 이전에 정리본을 영어로 업로드해두어, 간단한 정의에 대해 먼저 다시 살펴보고, Python을 활용해 intensity meausre와 같은 point process 데이터의 주요 특징을 어떻게 분석하는지 다루어보도록 하겠다.

Point Process

Definition

(Spatial) Point process 는 한마디로 integer-valued random measure로 정의될 수 있다. 즉, 확률공간 $(\Omega,\mathcal{F},P)$이 주어지고 $\mathbb{R}^{d}$의 부분가측공간 $(S,\mathcal{S})$ 이 주어질 때 point process $\xi:\Omega\times \mathcal{S}\to \mathbb{Z}_{+}$ 는 다음과 같이 정의된다.

  1. 임의의 $\omega\in \Omega$ 에 대해 $\xi(\omega,\cdot)$ 은 locally finite인 $(S,\mathcal{S})$에서의 측도이다.
  2. 임의의 $B\in\mathcal{S}$ 에 대해 $\xi (\cdot, B)$ 은 양의 정수값을 갖는 확률변수이다.

이때 2번의 확률변수를 $N(B)$ 라고도 표기하며 count function이라고 부른다. 1번의 측도는 일종의 counting measure가 된다. 또한, 다음과 같이 임의의 $B\in \mathcal{S}$에 대한 측도 $\mu$를 정의할 수 있는데, 이를 intensity measure라고 한다.

\[\mu(B) = \mathrm{E}N(B) = \int_{B}\lambda(\xi)d \xi\]

적분 형태로 표현되는 intensity measure의 함수 $\lambda(\xi)$를 intensity function이라고 한다.

PySAL

R에서는 공간통계 방법론들을 다루기 위해 sparr, spatstat등 다양한 패키지가 존재하지만, 파이썬에서는 pysal 패키지와 geopandas를 이용하게 된다. pysal 패키지는 공간통계의 방법론들을 여러 세부 패키지들로 포함하고 있으며, geopandas는 pandas 패키지를 기반으로 지리적 데이터를 다룰 수 있게 만든 자료 관리 패키지이다.

import geopandas as gpd
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import pysal as ps
import shapely
import libpysal

예제 데이터 로드

Pysal에서는 여러가지의 예제 데이터셋을 제공하는데, libpysal.examples.available() 코드를 실행시켜 가능한 목록들을 데이터프레임으로 출력할 수 있다. 이번 글에서는 샌프란시스코의 범죄 데이터를 나타내는 예제 데이터셋 SanFran Crime을 사용해보도록 하겠다. 우선, 다음과 같이 코드를 실행시키면 예제 데이터셋에 대한 대략적인 분포나 구성 등을 확인할 수 있다.

# example data : San Francisco crime data

libpysal.examples.explain('SanFran Crime')

위와 같이 interactive한 화면으로 데이터 분포를 확인할 수 있다. 이제 데이터 파일을 로드해보자. SanFran Crime 데이터는 기본으로 다운로드 되어 있지 않으므로, 다음 코드를 실행시켜 다운로드하고, 파일명 리스트를 출력해보도록 하자.

# Download the data
libpysal.examples.load_example('SanFran Crime')

# Load
from libpysal.examples import load_example

data = load_example('SanFran Crime')

data.get_file_list()

파일명 리스트에서 .shp파일을 찾아 로드하면 되는데, 이는 다음과 같이 geopandas 패키지를 이용하면 된다. 여기서는 마약범죄와 관련된 데이터를 로드했다. drugs 데이터프레임은 개별 범죄의 발생지점 좌표를 나타내는 데이터이며, blocks는 샌프란시스코 지역을 나타내는 데이터프레임이다.

# Load the shapefile
drugs = gpd.read_file(data.get_path('sf_drugs.shp'))
blocks = gpd.read_file(data.get_path('SFCrime_blocks.shp'))

이제, geodataframe의 .plot() 메소드를 이용하여 시각화를 진행할 수 있다. 다음과 같은 코드로 시각화가 가능하다.

# Plot
fig, ax = plt.subplots(figsize=(12,10))
blocks.boundary.plot(ax=ax)
drugs.plot(ax=ax, color='red', markersize=1)
plt.show()

그런데, 실제 출력된 결과(위)를 확인해보면 시각화가 제대로 이루어지지 않았음을 확인할 수 있다. 이는 두 데이터프레임 blocks, drugs의 좌표계 형식이 일치하지 않기 때문이다. (geopandas 데이터의 시각화 오류가 발생하는 경우 대부분 이러한 경우일 것이다.) 이를 해결하기 위해서 좌표계를 나타내는 crs 속성을 일치시켜 주어야 하는데, 여기서는 blocks의 좌표계를 drugs의 좌표계로 맞춰주었다.

# Check coordinates
print(blocks.crs) # EPSG:4269 
print(drugs.crs) # EPSG:2227 -- 서로 다름

# Reproject
blocks = blocks.to_crs(drugs.crs)

이제 다시 시각화를 진행하면 정상적으로 표시되는 것을 확인할 수 있다.

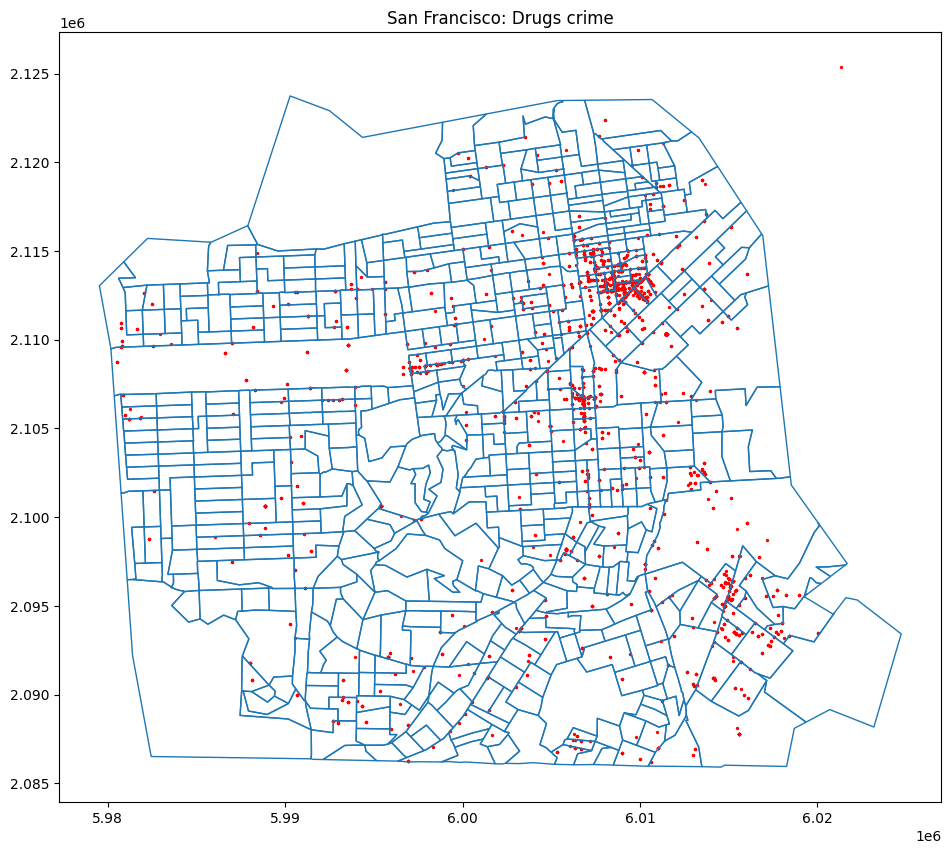
Point Process

Pysal에서 point process를 다루기 위해서는 서브패키지 pointpats의 모듈을 활용해야 한다. pointpats 패키지의 PointPattern 객체를 사용하면 point process data(point pattern)를 클래스로 정의할 수 있다. 문제는, geopandas에서 사용하는 shapely 기반 오브젝트를 그대로 사용할 수가 없어서, numpy 배열로 변환 후 libpysal.cg의 클래스로 변환하는 작업이 필요하다. 이는 다음과 같이 진행할 수 있다.

from pointpats import PointPattern, PointProcess, PoissonPointProcess, as_window

# to numpy array
poly = libpysal.cg.Polygon(list(blocks.unary_union.exterior.coords))
points = np.array([libpysal.cg.Point(p) for p in drugs.geometry.apply(lambda p: (p.x, p.y))])

# Create a point pattern and window
window = as_window(poly)
pp = PointPattern(points, window)

# Plot
pp.plot(window=True, hull=True, title='San Francisco: Drugs crime')
plt.show()

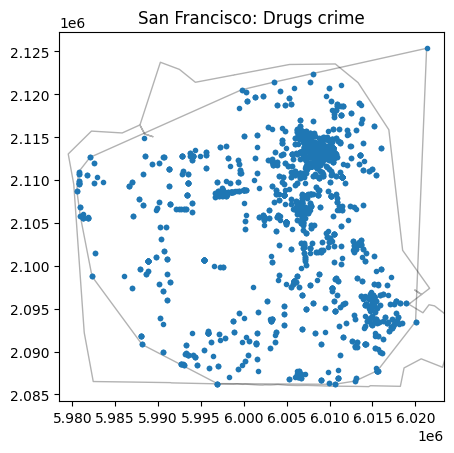
여기서 window 객체는 분석 대상이 되는 지역($W\subseteq \mathbb{R}^{d}$)를 의미한다. pp.window를 이용해 윈도우 객체의 호출이 가능하다.

pp.window.area
# 1328485407.66687 : 윈도우 영역의 넓이(m^2)

Intensity

Point pattern 데이터의 intensity를 측정하는 것은 가장 기본적이면서도 중요한 과정이다.

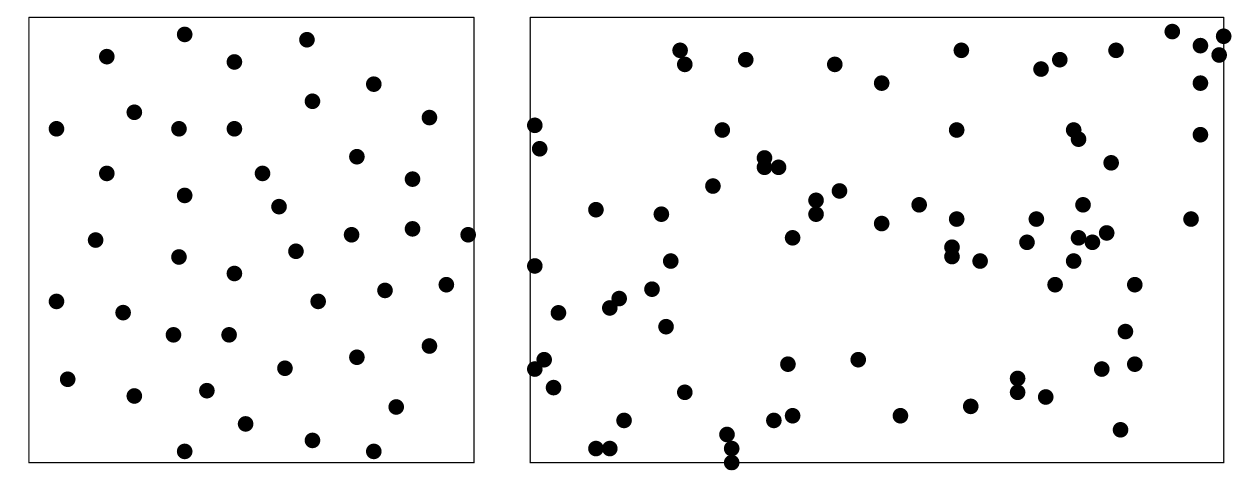
왼쪽 그림과 같이 균일하게 분포되어 있는 형태는 homogeneous intensity를 갖는다고 말한다. 그러나 오른쪽 그림에서와 같이, 균일성을 명확하게 파악하기 어려운 경우에는 해당 intensity가 homogeneous한지 inhomogeneous한지 쉽게 파악하기 어렵다. 이러한 경우, intensity function $\lambda(\xi)$를 주어진 데이터로부터 추정하는 과정이 필요하다.

Intensity의 가장 간단한 추정량을 생각해보면, 다음과 같이 적률추정량의 개념처럼 접근할 수 있다. 이는 주어진 point pattern이 homogeneous하다고 가정하고 intensity function을 상수로 가정하는 것이다 (이를 complete spatial randomness 라고도 한다).

\[\hat\lambda(\xi) = \frac{n}{\left\vert W\right\vert}\]

여기서 $W$는 window area를 의미한다. 다음과 같이 계산하거나, .lambda_window 속성으로 호출할 수 있다.

intensity = pp.n / pp.window.area
print(intensity)
print(pp.lambda_window)

# 2.9334157360780046e-06

이 외에도, 윈도우의 convex hull(위 plot 참고)을 이용하거나, minimum bounding box를 사용하여 계산할 수도 있다.

print(pp.lambda_mbb) # 2.4379572813841635e-06
print(pp.lambda_hull) # 3.2061868363282854e-06

CSR Point pattern

우리가 가지고 있는 point pattern 데이터가 실제 complete spatial randomness를 가진 Poisson point process 데이터와 다른지 확인하기 위해, 다음과 같이 Poisson point process 객체를 생성하여 시뮬레이션을 통해 샘플 패턴을 얻을 수 있다.

np.random.seed(1)

poisson = PoissonPointProcess(window=pp.window, samples=1, n=300, asPP=True)
pp_csr = poisson.realizations[0]

pp_csr.plot(window=True, hull=True, title='San Francisco: Drugs crime (CSR)')

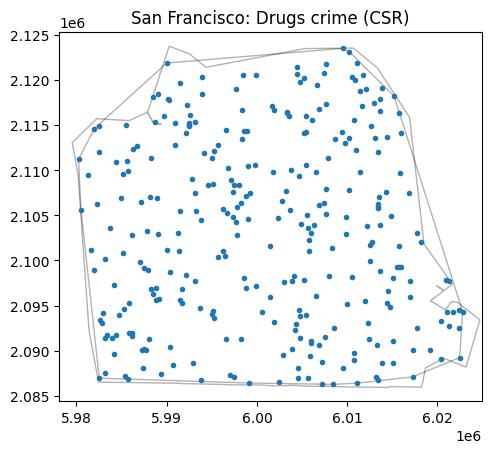
앞선 plot과 비교해보면, 우리의 데이터가 inhomogeneity를 갖는다는 것은 쉽게 알 수 있다.

Nonparametric estimation of Inhomogeneity

적절한 시각화를 통해 주어진 point pattern 데이터가 inhomogeneous한 intensity를 갖는다는 것을 확인했다면, 비모수적nonparametric 방법을 통해 intensity function $\lambda(\xi)$를 추정할 수 있다. 여기서는 quadrat counting과 커널밀도추정 방법을 살펴보도록 하겠다.

Quadrat counting

Quadrat은 사각형 격자를 의미하는데, quadrat counting이란 주어진 윈도우를 일정한 (사각형) 격자들로 나누어 각 격자에 속한 점들의 개수를 세는 간단한 방법론이다. 비교적 간단한 방법처럼 보일 수 있지만, 해당 영역에서 CSR point pattern에서의 기대 도수와 실제 도수를 비교하는 방법을 이용해 카이제곱 검정과 같은 방법론을 구현할 수 있다.

코드는 다음과 같다. nx,ny는 각각 가로 격자 수, 세로 격자 수를 의미한다.

import pointpats.quadrat_statistics as qs

# Quadrat test
q = qs.QStatistic(pp, shape='rectangle', nx=10, ny=10)
ax = q.plot()
plt.title('San Francisco: Drugs crime (Quadrat test)')
plt.show()

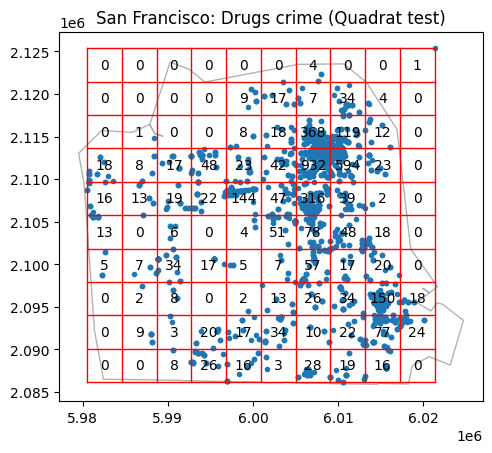
Chi-squared test

카이제곱 검정은 다음과 같은 검정통계량으로 정의된다.

\[\chi^{2}=\sum_{j}\frac{(\text{observed - expected})^{2}}{\text{expected}}= \sum_{j}\frac{(n_{j}-\hat \lambda a_{j})^{2}}{\hat \lambda a_{j}}\]

여기서 $\hat \lambda$는 CSR 가정 하에서 추정된 homogeneous intensity이고, $a_{j}$는 각 quadrat의 넓이를 의미한다. 귀무가설 $H_{0}$은 point process가 CSR이라는 것이고, 대립가설 $H_{1}$은 inhomogeneous intensity임을 의미한다. pysal에서는 다음과 같은 속성으로 확인가능하다.

print(q.chi2) # 36081.88119065948 
print(q.chi2_pvalue) # 0.0

검정 결과 유의수준 5%에서 귀무가설을 기각할 수 있다.

Kernel estimation

만일 point process가 intensity function $\lambda(\xi)$를 갖는다면, intensity function의 커널추정량을 계산할 수 있다. 커널함수 $k(s)$ 에 대해, 다음과 같은 추정량 형태들이 가능하다.

  • Uncorrected
\[\hat \lambda^{(0)}(s) = \sum_{i=1}^{n}k(s-x_{i})\]
  • Uniformly corrected
\[\hat \lambda^{U}(s) = \frac{1}{e(s)}\sum_{i=1 }^{n}k(s-x_{i})\]

  • Diggle’s correction

    \[\hat \lambda^{D}(s) = \sum_{i=1}^{n} \frac{1}{e(x_{i})}k(s-x_{i})\]

    여기서 $e(s)=\int_{W}k(s-u)du$ 를 의미한다.

pysal에는 pointpats.plot_density 함수를 이용해 커널추정량을 구할 수 있는데, 보정이 이루어진 추정치는 내장되어 있지 않다. 따라서 boundary effect가 존재할 수 있다 (경계 근방의 intensity가 낮게 도출되는 현상).

fig, ax = plt.subplots()
cs = plot_density(ax=ax, data=drugs, bandwidth=3000, cmap='Reds', fill=True)
cbar = fig.colorbar(mappable=None, orientation='vertical', cax=None, ax=ax, cmap='Reds')
blocks.boundary.plot(ax=ax, lw=0.2)
plt.title('Kernel estimation with $h=3000$')
plt.show()

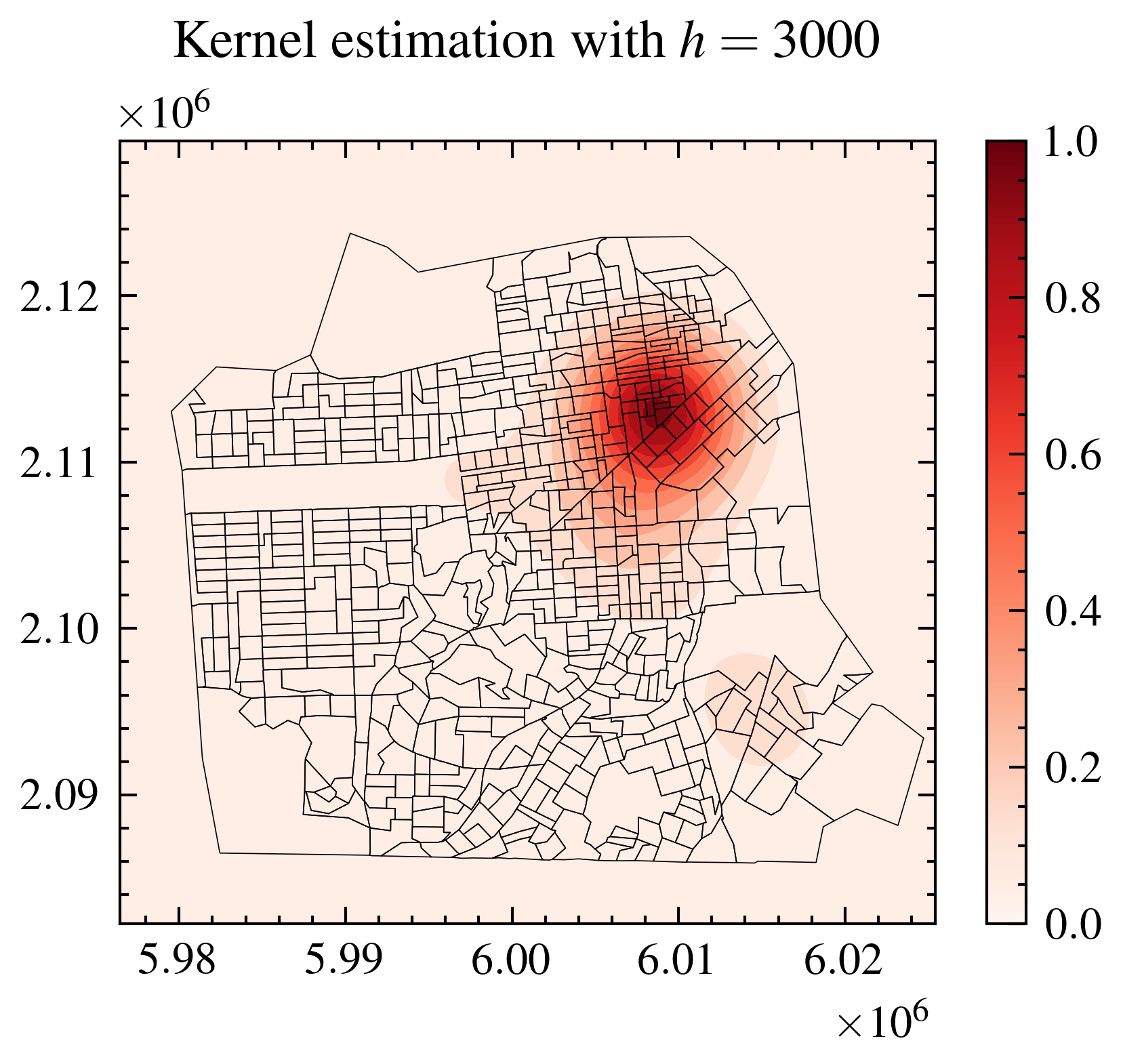
Kernel estimation의 경우 smoothing parameter $h$, 즉 대역폭bandwidth 설정의 문제가 있다. $h$ 값을 크게 설정할 경우 oversmoothing 된 intensity function이 도출될 수 있고, 작게 설정할 경우 매우 불규칙한 intensity를 얻게 된다. 물론 다른 비모수적 방법론들과 마찬가지로 optimal smoothing parameter가 존재하는데, 이에 대해서는 추후 다루도록 하겠다.

References

Leave a comment