Transfer Learning and Fine Tuning

파인 튜닝^{Fine Tuning}이란 개념은 LLM의 등장과 함께 더욱 주목받게 된 개념이다. 이전까지는 한번 모델을 학습시키고 나면, 해당 모델의 파라미터를 고정시키고 새로운 데이터 $\mathbf x’$에 대해 예측을 수행하는 방식이 일반적이었다. 그러나, 모델의 규모가 매우 커지면서(특히 Transformer의 등장 이후) 파라미터 수가 기하급수적으로 증가하였고 이로 인해 새로운 데이터에 대해 모델을 처음부터 학습시키는 것은 매우 비효율적인 방법이 되었다. 따라서, 기존 모델의 파라미터를 새로운 데이터에 대해 조금씩 조정하는 방법이 주목받게 되었다. 이를 Fine tuning이라고 한다.

Fine tuning은 전이학습^{Transfer Learning}의 한 형태로 볼 수 있다. 전이학습은 기존의 학습된 모델을 새로운 데이터셋에 적용하는 방법이다.

Transfer Learning

Source distribution $p$에 대해 labeled data $\mathcal D^s = \lbrace (\mathbf x_n, y_n) \sim p : n=1,\ldots,N_s\rbrace $ 가 주어지고, target distribution $q$에 대해 labeled data $\mathcal D^t = \lbrace (\mathbf x_n, y_n) \sim q : n=1,\ldots,N_t\rbrace $가 주어졌다고 하자. 우리가 관심있는 것은 target distribution $q$에 대한 예측 모델 $f(\mathbf x)$를 학습하는 것이다.

이에 대해 Empirical risk minimization(ERM) 관점은

\[R(f,q) = \mathbb E_q[\ell(f(\mathbf x), y)]\]

을

\[\hat R(f, \mathcal D^t) = \frac{1}{N_t} \sum_{n=1}^{N_t} \ell(f(\mathbf x_n), y_n)\]

형태로 근사하는 것이다. 만일 $N_t$가 충분히 크다면 일반적인 ERM 방법을 사용하여 데이터셋 $\mathcal D^t$에 대해 모델 $f$를 학습시킬 수 있다. 그러나, $N_t$가 작은 경우에는 모델 $f$를 학습시키기 어려울 수 있다. 이때, source data $\mathcal D^s$를 일종의 규제(regularization)로 사용하여 모델 $f$를 학습시키는 방법이 전이학습이다.

Pre-train and Fine-tune

가장 널리 사용되며, 가장 간단한 전이학습 방법은 fine tuning이다. 우선, pre-training 단계에서는

\[f^s = \mathop{\arg\min}\limits_{f\in\mathcal F} \hat R(f, \mathcal D^s)\]

을 학습시키고, fine-tuning 단계에서는

\[f^t = \mathop{\arg\min}\limits_{f\in\mathcal F} \hat R(f, \mathcal D^t) + \lambda\Vert f - f^s \Vert\]

와 같은 형태로 target distribution에 대한 모델을 얻는다. 이때, $\lambda$는 규제항의 강도를 조절하는 하이퍼파라미터이며, $\Vert f - f^s \Vert$는 두 함수 $f$와 $f^s$의 거리를 나타낸다.

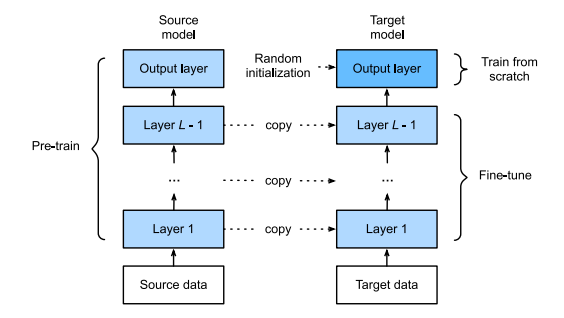Illustration of fine-tuning(Murphy, 2022)

구체적으로, pre-training 단계에서는 대규모 데이터셋(large source dataset) $\mathcal D_p$에 대해 파라미터 $\boldsymbol \theta$를 학습시키고, fine-tuning 단계에서는 라벨링이 이루어진 작은 데이터셋(small labeled target dataset)에 대해 파라미터 $\boldsymbol \theta$를 조정한다. 이때, fine-tuning 단계에서는 pre-training 단계에서 학습된 파라미터 $\boldsymbol \theta$를 초기값으로 사용한다.

만일 ‘멸종위기 조류의 이미지’를 분류하는 모델을 만들고자 한다면, 해당 모델을 처음부터 학습시키는 것은 어려울 것이다. 멸종위기 조류의 이미지 데이터셋은 매우 적을 것이기 때문이다. 따라서, 이러한 경우 fine-tuning을 사용하여 기존의 이미지 분류 모델을 사용하는 것이 효율적일 것이다.

우선, ImageNet 데이터셋 등을 이용해 대규모 데이터셋 $\mathbf x\in \mathcal X_p$ (ex. 전체 조류 이미지) 대해 CNN 모델 $p(y\vert \mathbf x, \boldsymbol\theta_p)$을 학습시킨다. 이후 멸종위기 조류의 이미지 데이터셋 $\mathbf x’\in \mathcal X_q$에 대해 fine-tuning을 수행한다. 이때, 두 input domain $\mathcal X_p$와 $\mathcal X_q$는 동일하거나 변환가능해야 한다. 그렇지 않을 경우, domain adaptation 기법을 사용해야 한다.

그러나 일반적으로 fine tuning을 진행하는 목적은 다른 종류의 task를 수행하는 것이기 때문에, output domain $\mathcal Y_p$와 $\mathcal Y_q$는 다르게 설정된다. 따라서, fine-tuning에서는 output layer의 파라미터는 초기화되어야 한다 (pre-training 단계에서 학습된 파라미터를 사용하지 않는다, 위 그림 참고).

예를 들어 pre-trained model이 $p(y\vert \mathbf x, \boldsymbol\theta_p)=\mathcal S(y\vert \mathbf W_2 h(\mathbf x;\theta_1) + b_2)$ 형태로 주어진다면, fine-tuning 단계에서는 $q(y\vert \boldsymbol \theta_q)=\mathcal S(y\vert \mathbf W_3 h(\mathbf x;\theta_1) + b_3)$ 형태로 output layer의 파라미터를 다르게 지정한다.

Pre-training

Pre-training 단계는 supervised learning이나 unsupervised learning 방법이 사용된다.

Supervised Pre-training

이미지 분류 혹은 CNN 기반 모델을 사용하는 경우, pre-train 단계에서 ImageNet 데이터를 사용하는 것이 가장 일반적이라고 한다. ImageNet 데이터셋의 경우 1000개의 클래스로 레이블이 주어지므로 supervised learning 방법을 사용할 수 있다. 다만, fine-tuning 단계가 natural image와 다른 경우(ex. 영상의학 이미지) pre-train의 효과가 떨어질 수 있다.

Unsupervised Pre-training

CNN에서 이미지 기반의 supervised 방법을 사용하는 것과는 달리, 일반적으로는 unlabeled data를 얻기가 훨씬 쉽기 때문에, unsupervised 방법을 사용한다. Unsupervised pre-training을 self-supervised learning^SSL이라고도 하는데, 이는 모델이 자신의 입력 데이터에 대해 레이블을 생성하는 방법을 의미한다. 예를 들어, 이미지 데이터셋에 대해 모델이 이미지를 회전시키거나, 이미지의 일부를 가려서 원본 이미지를 복원하는 방법을 사용할 수 있다.

Imputation tasks

SSL의 한 방법으로 imputation을 수행하는 것이 있다. 입력 데이터 $\mathbf x$를 두 부분 $\mathbf x = (\mathbf x_1, \mathbf x_2)$로 나누고, 모델이 $\mathbf x_1$을 이용해 $\mathbf{\hat x}_2= f(\mathbf{x}_1, \mathbf{x}_2=\mathbf 0)$을 예측하도록 학습시킨다.

Contrastive learning

최근 가장 많이 사용되는 SSL 기법은 contrastive task를 사용하는 것이다. 기본적인 아이디어는 data pair $(\mathbf x, \mathbf x’)$를 사용해 모델이 같은 클래스에 속하는 data pair를 가깝게, 다른 클래스에 속하는 data pair를 멀게 만드는 방법이다.

대표적인 예시로 SimCLR(Simple Framework for Contrastive Learning of Visual Representations)가 있다. SimCLR는 입력 $\mathbf{x}\in \mathbb{R}^D$ 를 두 view $\mathbf{x}_1=t_1(\mathbf{x})$과 $\mathbf{x}_2=t_2(\mathbf{x})$로 변환하는데 이때 $t_1,t_2 : \mathbb{R}^D \to \mathbb{R}^D$는 랜덤한 augmentation을 수행하는 함수이다. 또한, 각 배치 내의 다른 데이터 $\mathbf{x}_1^-, \ldots, \mathbf{x}_K^- \in N(\mathbf{x})$를 사용해 positive pair $(\mathbf{x}_1, \mathbf{x}_2)$와 negative pair $(\mathbf{x}_1, \mathbf{x}_1^-), \ldots, (\mathbf{x}_1, \mathbf{x}_K^-)$를 생성한다.

이후 feature mapping $F: \mathbb{R}^D \to \mathbb{R}^E$를 사용해 각 view를 임베딩하고, 이를 이용해 각 positive pair와 negative pair의 similarity를 계산한다. 이때, positive pair의 similarity는 높게, negative pair의 similarity는 낮게 만드는 방향으로 학습을 진행한다. 이를 위해 다음과 같은 loss function을 사용한다.

\[J = F(t_1(\mathbf{x}))^\top F(t_2(\mathbf{x})) - \log \sum_{\mathbf{x}_i^-\in N(\mathbf x)} \exp(F(t_1(\mathbf{x}))^\top F(\mathbf{x}_i^-))\]

References

K. P. Murphy, Probabilistic machine learning: an introduction. in Adaptive computation and machine learning. Cambridge, Massachusetts London, England: The MIT Press, 2022.
K. P. Murphy, Probabilistic machine learning: advanced topics. in Adaptive computation and machine learning series. Cambridge, Massachusetts: The MIT Press, 2023.
T. Chen, S. Kornblith, M. Norouzi, and G. Hinton, “A Simple Framework for Contrastive Learning of Visual Representations.” arXiv, Jun. 30, 2020. doi: 10.48550/arXiv.2002.05709.