Generative Models and GAN

Generative Adversarial Networks

이번 글에서는 GAN 모델을 다루고자 한다. 다만, 일반적으로 GAN이 정의되는 방식 대신, 생성형 모델 중 implicit model에서 목적함수를 정의하는 방식을 기반으로 GAN의 목적함수가 도출되는 과정을 살펴보고자 한다.

Generative Models

생성 모델^{Generative Models}이란, 데이터의 분포($p(x)$ 혹은 $p(x\vert c)$)를 학습하여, 새로운 데이터를 생성하는 모델이다. 최근에는 딥러닝에 기반한 생성 모델들을 생성형 인공지능^{Generative AI}라고 부르며, 널리 사용하는 목적으로는 다음과 같은 것들이 있다.

• $c = \text{text prompt}$, $x=\text{image}$ : 텍스트를 입력하면, 해당하는 이미지를 생성 (ex. StableDiffusion)
• $c = \text{sequence of English}$, $x=\text{sequence of Korean}$ : 영어 문장을 입력하면, 한국어 문장을 생성 (sequence to sequence)

생성 모델은 크게 다음과 같은 두 분류로 나눌 수 있다.

Type of Probabilistic Generative models

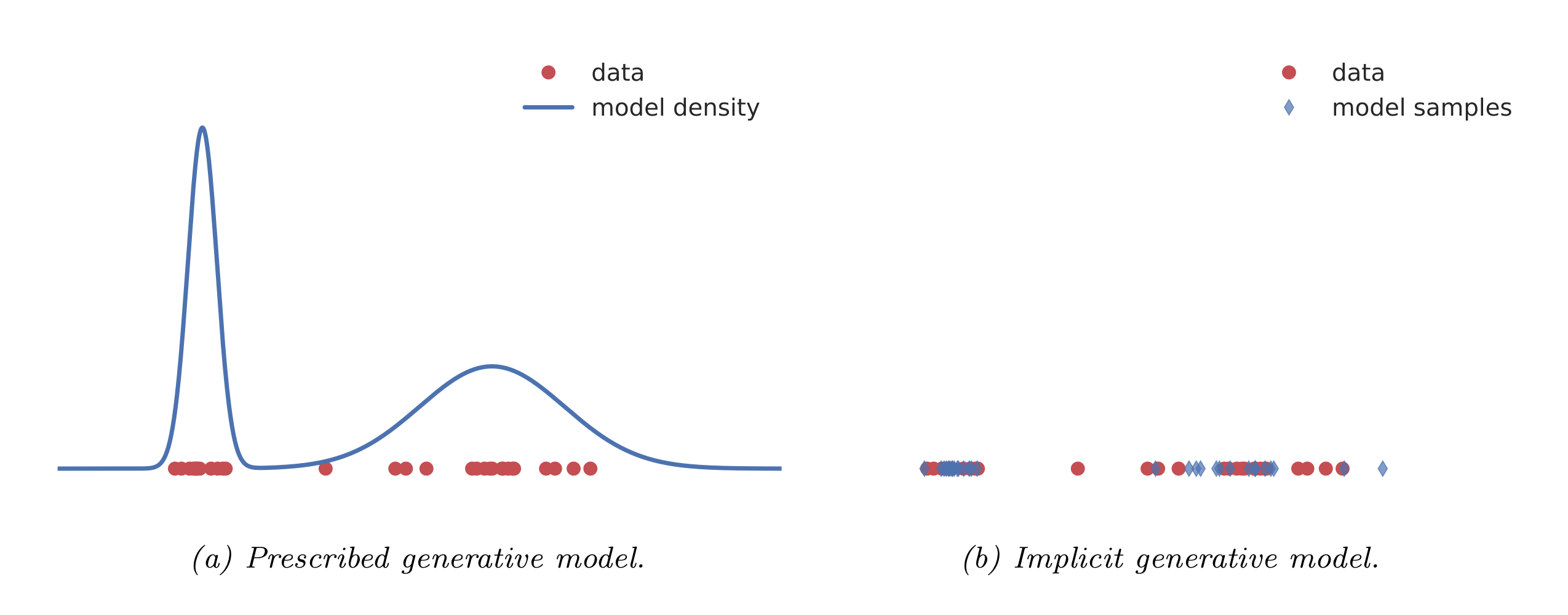
명시적 모델^{Explicit probabilistic models}은 주어진 데이터로부터 데이터가 생성되는 확률분포를 어떠한 모수 $\theta$를 사용한 가능도로 나타내는 것을 말한다 (그림 a). 예를 들어, VAE의 경우 생성모델의 가능도를 학습 과정에서 직접 이용하기 때문에, 이러한 구분에 속한다. 반면, 암시적 모델^{Implicit probabilistic models}은 데이터의 확률분포를 학습하기보다는, 직접적으로 데이터를 생성하는 확률적인 과정을(stochastic process는 아님) 정의한다 (그림 b). 암시적 모델의 표현은 다음과 같이 이루어진다.

Implicit Models

암시적 모델은 VAE와 유사하게, 잠재변수 $Z$를 가정하고 deterministic function $G_{\theta}: \mathbb{R}^{p}\to \mathbb{R}^{k}$ 를 사용하여 잠재변수를 변환한다. 다만, 앞서 언급한대로 가능도를 직접 사용하지 않고, output space에 대한 가능도를 다음과 같이 잠재변수의 확률밀도로부터 정의한다.

\[\begin{align} \mathbf{x}&= G_{\theta}(\mathbf{z}')\quad \mathbf{z}'\sim q(\mathbf{z})\\ q_{\theta}(\mathbf{x}) &= \frac{\partial}{\partial x_{1}} \cdots \frac{\partial}{\partial x_{d} }\int_{\lbrace G_{\theta}(\mathbf{z})\leq \mathbf{x}\rbrace } q(\mathbf{z})d \mathbf{z} \end{align}\]

함수 $G$에 심층신경망 구조를 주어 유연한 모델을 가정하면, 이를 generative neural sampler 혹은 generator network라고 한다. 다만, $q_\theta$ 의 적분이 intractable하기 때문에 그래디언트에 기반한 최대가능도 추정 방향으로의 학습이 불가능하다. 따라서 GAN에서는 샘플링 방법을 이용하여 학습을 진행하는데, 그 방식은 다음과 같다.

Learning by Comparison

일반적으로 대부분의 머신러닝 모델은 최대가능도를 기반으로 학습한다. 대부분의 경우 가능도를 최대화하면, 알려져있지 않은 실제 데이터 분포 $p^{\ast}$와 이를 모델링하는 $q_{\theta}$ 간의 KL divergence 역시 최소화되기 때문이다. 다만 암시적 모델의 경우 $q_{\theta}$를 직접 구하는 것이 불가능하므로, 샘플을 기반으로 한 학습을 진행해야 한다.

따라서, 목적함수 $\mathcal{D}(p^{\ast},q)$ 는 다음 성질을 만족시켜야 한다.

1. $\mathop{\arg\min}\limits_{q} \mathcal{D}(p^{\ast},q) = p^{\ast}$ : 목적함수의 최적화문제를 푸는 과정이 실제 데이터 분포를 학습해야 한다.
2. $q_{\theta}$ 를 직접 사용하는 것이 아닌, 샘플을 이용해야 한다.
3. 계산비용이 크지 않아야 한다.

조건 1의 경우 대부분의 metric, divegence는 그 정의로부터 성립한다. 다만 2와 3을 만족시키지는 못한다. 이를 해결하기 위해 도입된 것이 discrimator $D$로, 어떤 metric, divergence로 직접 비교하는 대신 비교를 수행하는 모델을 도입한다는 것이다. 이를 다음과 같이 나타낼 수 있다.

\[\mathcal{D}(p^{\ast},q) = \arg\max_{D}\mathcal{F}(D,p^{\ast},q)\]

여기서 $\mathcal{F}$는 $p^{\ast},q$ 의 샘플에 의존하는 범함수를 의미한다. 위 식의 의미를 해석해보면, 데이터 분포 $p^{\ast}$와 $q$를 비교하기 위해 학습되는 $D$ 라는 discrimator를 이용해 $\mathcal{F}$라는 범함수로 비교에 대한 정도를 측정하는 것을 의미한다.

Discrimator에 심층신경망과 같은 parameterized model $D_{\phi}$을 부여하면, 우리는 위 식을 $\phi$에 대한 최적화 문제로 나타낼 수 있게 된다. 또한, $D_{\phi}$를 사용함으로써 실제 목적함수 $\mathcal{D}(p^{\ast},q_{\theta})$ 를 $\mathcal{F}$로 근사할 수 있게 된다.

$\mathcal{F}$의 예로 다음과 같은 기댓값 형태를 고려할 수 있다.

\[\mathcal{F}(D_{\phi},p^{\ast},q_{\theta}) = \mathrm{E}_{p^{\ast}}f(\mathbf{x},\phi) + \mathrm{E}_{q_{\theta}}g(\mathbf{x},\phi )\]

$f,g$는 적절한 임의의 함수를 나타낸다. 암시적 모델의 경우를 고려하면 다음과 같다.

\[\mathcal{F}(D_{\phi},p^{\ast},q_{\theta}) = \mathrm{E}_{p^{\ast}}f(\mathbf{x},\phi) + \mathrm{E}_{q(z)}g(G_\theta(\mathbf{z}),\phi)\]

따라서, $\mathcal{F}$는 $q_\theta(\mathbf{x})$에 기반하지 않으며 Monte Carlo 근사 역시 가능하다.

\[\mathcal{F}(D_{\phi},p^{\ast},q_{\theta}) = \frac{1}{N}\sum_{i=1}^{N}f(\hat x_{i},\phi)+ \frac{1}{M}\sum_{i=1}^{M}g( G_{\theta}(\hat z_{i}),\phi)\quad \hat x_{i}\sim p^{\ast},\hat z_{i}\sim q\]

아래는 $\mathcal{F}$의 예시 중 하나로 밀도비 추정^DRE를 소개하는데, 이는 GAN의 기본 원리가 된다.

GAN

Density Ratio Estimation

두 확률밀도 $p^{\ast},q$ 를 비교하기 위해 밀도함수의 비 $r(x) = \frac{p^{\ast}(x)}{q_{\theta}(x)}$를 생각해보자. 이때, 다음과 같이 discrimator $D(x)$ 를 이용하면 다음과 같이 밀도추정 문제를 이진분류 문제로 변환할 수 있다.

\[\begin{align} \dfrac{p^{\ast}(x)}{q_{\theta}(x)} &= \frac{D_{\phi}(x)}{1-D_{\phi}(x)} \tag{1} \end{align}\]

여기서 $D_{\phi}(x)\in[0,1]$는 주어진 샘플이 $p^{\ast}$으로부터 얻어진 샘플인지, $q_{\theta}$로부터의 샘플인지를 구별하는 역할을 수행한다. 즉, 베르누이 확률변수 $Y$에 관한 조건부확률 $P(Y=1\vert X=x)$ 을 모델링한다고 볼 수 있다.

BCE^{Binary cross entropy} 손실함수를 이용하면, 목적함수를 다음과 같이 쓸 수 있다.

\[\begin{align} V(q_{\theta},p^{\ast}) &= \arg\max_{\phi} \mathrm{E}_{p(x\vert y) p(y)}[y\log D_{\phi}(x)+(1-y)\log(1-D_{\phi}(x))]\\ &= \arg\max_{\phi} \frac{1}{2}\mathrm{E}_{p^{\ast}}\log D_{\phi}(x) + \frac{1}{2}\mathrm{E}_{q_{\theta}}\log(1-D_{\phi}(x)) \end{align}\]

또한, 식 $(1)$로부터 optimal discrimator $D^{\ast}$를 다음과 같이 구할 수 있다.

\[D^{\ast}(x) = \frac{p^{\ast}(x)}{p^{\ast}(x) + q_{\theta}(x)}\]

이를 위 목적함수에 대입하면, 목적함수 $V$를 다음과 같이 변환할 수 있다.

\[\begin{align} V(q_{\theta},p^{\ast}) &= \frac{1}{2}\mathrm{E}_{p^{\ast}}\left[ \log \frac{p^{\ast}(x)}{p^{\ast}(x)+q_{\theta}(x)}\right] + \frac{1}{2} \mathrm{E}_{q_{\theta}}\left[ \log \left(1- \frac{p^{\ast}(x)}{p^{\ast}(x)+q_{\theta}(x)}\right)\right]\\ &= \frac{1}{2}\mathrm{KL}\left(p^{\ast} \bigg\Vert \frac{p^{\ast} + q_{\theta}}{2}\right) + \frac{1}{2}\mathrm{KL}\left(q_{\theta} \bigg\Vert \frac{p^{\ast} + q_{\theta}}{2}\right)-\log 2\\ &= JSD(p^{\ast},q_{\theta}) - \log 2 \end{align}\]

여기서 $JSD(p,q)$ 는 Jensen-Shannon divergence를 의미한다. 즉, 위 변환으로부터 BCE 손실함수의 목적함수를 최소화하는 문제가 Jensen-Shannon divergence를 최소화하는 문제로 해석될 수 있음을 알 수 있다. 따라서, 암시적 모델에서 분포에 대한 직접적인 계산 없이도 샘플을 이용한 이진분류문제를 해결하면 분포가 학습이 가능해진다. 즉, 앞서 살펴본 조건 1-3을 모두 만족한다.

Intractable estimation problem (Minimizing divergence) $\to$ Optimization problem of a classifier $D$

Learning Parameters

이제, 생성모델의 파라미터 $\theta$를 학습하는 방법을 생각해보자. Optimal classifier(discriminator) $D^{\ast}$로부터 다음 최적화 문제를 얻을 수 있다.

\[\begin{align} \min_{\theta}JSD(p^{\ast},q_{\theta}) &= \min_{\theta}V^{\ast}(q_{\theta},p^{\ast}) + \log 2\\ &= \min_{\theta} \frac{1}{2}\mathrm{E}_{p^{\ast}}\log D^{\ast}(x) + \frac{1}{2}\mathrm{E}_{q_{\theta}}\log(1-D^{\ast}(x)) + \log 2 \end{align}\]

다만, optimal classifier를 직접 구할 수 없으므로(bayes classifier를 생각), 신경망을 도입한 $D_{\phi}$를 근사 모형으로 사용하기로 한다. 이를 도입할 경우, 다음과 같이 min-max optimization problem을 얻는다.

\[\min_{\theta}\max_{\phi} \frac{1}{2}\mathrm{E}_{p^{\ast}}\log D_{\phi}(x) + \frac{1}{2}\mathrm{E}_{q_{\theta}}\log(1-D_{\phi}(x))\]

암시적 모델에서의 Generator $G$를 도입하면, 다음과 같다.

\[\min_{\theta}\max_{\phi} \frac{1}{2}\mathrm{E}_{p^{\ast}}\log D_{\phi}(x) + \frac{1}{2}\mathrm{E}_{q_{\theta}}\log(1-D_{\phi}(G_{\theta}(z)))\]

이는 GAN 논문에 (Goodfellow et al., 2014) 제안된 목적함수와 동일하다. 결국 GAN 모델이란 implicit model에서 Jensen-Shannon divergence를 $\mathcal{F}$로 사용하고, 이 과정에서 discriminator $D$를 binary classifier로 사용한 것으로 볼 수 있다.

Divergence의 종류를 변화시키거나(ex. $f$-divergence), BCE 손실함수 대신 다른 손실함수를 사용한 경우(ex. hinge loss)에 대해 각각 개별 연구로 제안된 바 있지만 궁극적으로 GAN 기반 모델들은 위와 같은 Implicit model의 프레임워크를 따른다고 볼 수 있다.

Image source : https://www.kdnuggets.com/2017/01/generative-adversarial-networks-hot-topic-machine-learning.html

일반적으로 GAN의 동작 원리를 설명할 때에는 위와 같은 형태로 $G,D$를 정의하여 설명한다. 앞서 GAN의목적함수를 도출해내는 과정이 결과적으로 GAN의 일반적인 설명과 일치함을 확인할 수 있다.

Density ratio estimation 대신, Integral Probability Metrics

\[I_\mathcal{F}(p^{\ast},q_{\theta})= \sup_{f\in\mathcal{F}} \left\vert \mathrm{E}_{p^{\ast}}f(x) - \mathrm{E}_{q_{\theta}}f(x)\right\vert\]

를 이용하여 밀도함수의 비교를 진행할 수 있다. 대표적인 것이 Wasserstein distance인데, 이러한 경우에 대해서는 추후 정리해 볼 예정이다.

References

• Murphy, K. P. (2023). Probabilistic machine learning: Advanced topics. The MIT Press.
• 서울대학교 딥러닝의 통계적 이해 강의노트
• Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., & Bengio, Y. (2014, June 10). Generative Adversarial Networks. arXiv.Org. https://arxiv.org/abs/1406.2661v1