Gaussian Differential Privacy

IntroductionPermalink

이번 포스트에서는 Gaussian Differential Privacy (Dong et al., 2022) 논문을 리뷰하며 Gaussian differential privacy에 대해 살펴보도록 하겠습니다. DP는 $(ϵ, δ)$ -DP 외에도 여러 relaxation가 존재합니다. Gaussian DP는 2022년 JRSSB에 위 논문으로부터 제안된 개념으로, 통계학에서 쓰이는 가설검정의 개념을 차용하여 DP를 구성합니다. 일반적인 DP는 privacy loss의 bound를 제한하는 방법으로 이루어지는 반면, Gaussian DP는 주어진 randomized mechanism $M$ 에 대해 출력값이 주어졌을 때, 이 출력값이 데이터셋 $D$ 으로부터 도출된 것인지(귀무가설) $D^{'}$ 으로부터 도출된 것인지를 검정합니다.

우선 논문의 순서대로, $f$ -DP 클래스를 먼저 정의한 후 이것의 일부분인 GDP에 대해 설명하도록 하겠습니다.

$f$ -DPPermalink

IndistinguishabilityPermalink

$(ϵ, δ)$ -DP, $(α, ϵ)$ -RDP 등 DP의 여러 변형이 존재하지만, 이들 모두는 근본적으로 mechanism $M$ 이 도출해낸 정보로부터 사용된 데이터셋이 $D, D^{'}$ 인지를 ( $D \sim D^{'}$ : neighboring) 구분하지 못하게끔 취하는 것입니다. 즉, DP를 만족하는 메커니즘은 사용자가 해당 메커니즘으로부터의 결과값을 얻었을 때, 해당 결과값이 이웃한 데이터셋 $D, D^{'}$ 중 어떤 것으로부터 도출된 것인지 구분할 수 없음^{indistinguishable}을 의미합니다.

그런데, 이러한 indistinguishability^비구별성는 통계학에서의 가설검정^{hypothesis testing}문제로 치환할 수 있습니다. 즉, 다음과 같은 가설검정 절차를 생각할 수 있습니다.

H_{0} : Underlying dataset is D vs H_{1} : Underlying dataset is D^{'}

만일 $M (D), M (D^{'})$ 의 확률분포가 각각 $P, Q$ 라고 하면 underlying dataset $D, D^{'}$ 를 구별하는 문제는 가설검정에서의 1종오류와 2종오류로 표현할 수 있습니다. 이는 임의의 기각 규칙^{rejection rule} $0 \leq ϕ \leq 1$ 에 대해

\begin{aligned} α_{ϕ} & = E_{P} ϕ & \dots Type 1 error \\ β_{ϕ} & = 1 - E_{Q} ϕ & \dots Type 2 error \end{aligned}

와 같이 나타낼 수 있습니다. 일반적으로 가설검정에서는 1종오류의 확률을 유의 수준으로 설정하고, 검정력을 최대화하는 방향으로 MP test 등을 구성합니다. 반면 DP에서의 관심 대상은 두 가설이 얼마나 구분 불가능한지이기 때문에, 1종오류와 2종오류의 trade-off를 고려하는 것이 주 목적이 됩니다. 이를 위해 다음과 같이 trade-off function을 정의합니다.

Trade-off functionPermalink

동일한 공간에서 정의된 두 확률분포 $P, Q$ 에 대해 trade-off function $T (P, Q) : [0, 1] \to [0, 1]$ 은 다음과 같이 정의됩니다.

T (P, Q) (α) = inf_{ϕ} {β_{ϕ} : α_{ϕ} \leq α}

즉, 이는 1종오류 확률 $α$ 를 고정시킨 후 가능한 최소의 2종오류 확률을 도출하는 함수입니다. 최소의 2종오류 확률을 구하는 것은 최대의 검정력을 구하는 것이므로( $Power = 1 - β$ ), 이는 Neyman-Pearson lemma의 가능도비 검정^{LRT test}으로 얻을 수 있습니다.

Trade-off function은 아래 그림과 같은 형태를 나타냅니다. ROC curve와 유사하게, 함수 아래 면적이 클 수록 두 분포의 구분이 어려움을 의미합니다. 또한, 가장 좋은(가장 구별하기 어려운) trade-off function은 identity function으로 $Id (α) = 1 - α$ 로 정의됩니다. 또한, identity function을 갖는 mechanism을 indistinguishable 하다고 정의합니다.

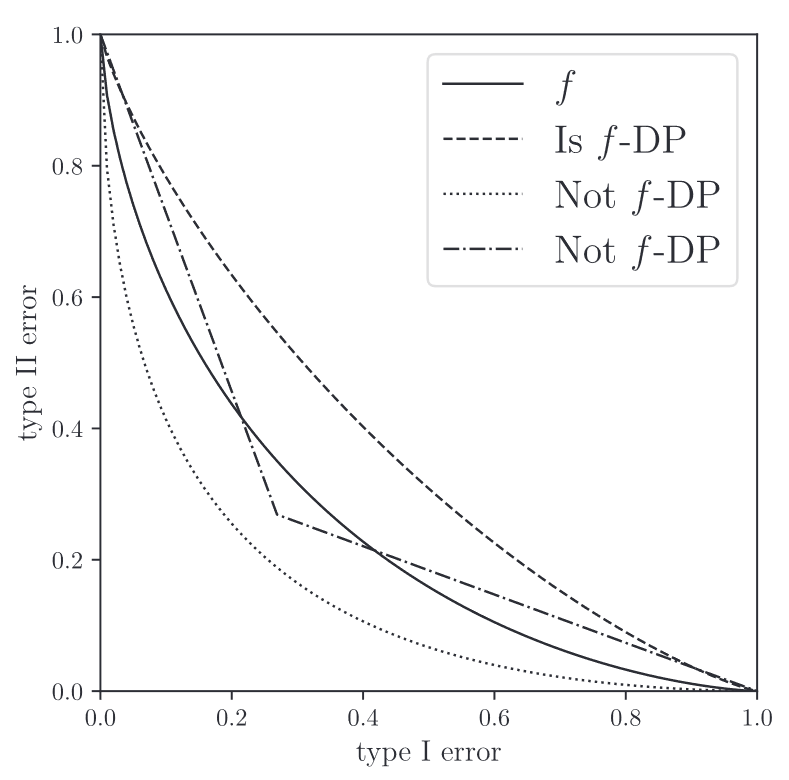Trade-off functions

따라서, 임의의 함수 $f$ 가 $f : [0, 1] \to [0, 1]$ 이고 convex, continuous, $f (x) \leq 1 - x$ 을 만족한다면 이를 trade-off function이라고 할 수 있습니다.

Definition $f$ -DPPermalink

앞서 정의한 trade-off function을 바탕으로, 다음과 같이 $f$ -DP를 정의합니다.

Trade-off function $f$ 에 대해 randomized mechanism $M$ 이 모든 이웃하는 데이터셋 $D \sim D^{'}$ 에 대해 다음을 만족하면 이를 $f$ -DP라고 정의합니다.

T (M (D), M (D^{'})) \geq f

이는 앞선 그림에서도 확인가능합니다. Trade-off function인 실선 $f$ 에 대해 모든 $x \in [0, 1]$ 에서 $f$ 위에 있는 점선만이 $f$ -DP를 만족합니다. 핵심은, $x \in [0, 1]$ 의 모든 구간에서 위 관계식을 만족해야 한다는 것입니다.

$f$ -DP와 다른 DP 정의들과의 차이점은, privacy parameter라고 볼 수 있는 $ϵ, δ, α$ 등의 값이 실수값으로 주어지는 것이 아닌, 함수 $f$ 로 주어진다는 것입니다. 실수값으로 명확히 주어지지 않기 때문에 사용에 어려움이 있는 정의라고 보일 수 있지만, 오히려 parameterization 과정에서 통계적 특성을 잃을 수 있다는 문제를 방지합니다.

Generalization of $(ϵ, δ)$ -DPPermalink

다음과 같이 $f_{ϵ, δ}$ 를 정의합니다.

f_{ϵ, δ} (α) = max (0, 1 - δ - e^{ϵ} α, e^{- ϵ} (1 - δ - α))

그러면 다음 관계가 성립합니다.

M is (ϵ, δ) -DP \Leftrightarrow M is f_{ϵ, δ} -DP

Gaussian Differential PrivacyPermalink

Gaussian differential privacy (GDP)는 앞서 정의한 $f$ -DP에서 trade-off function에 이용되는 두 분포가 정규분포인 경우에 해당됩니다. GDP를 정의하기 위해, 우선 다음과 같이 function $G$ 를 정의합니다.

\begin{aligned} G_{μ} (α) : & = T (N (0, 1^{2}), N (μ, 1^{2})) (α) \\ = Φ (Φ^{- 1} (1 - α) - μ) \end{aligned}

여기서 $Φ$ 는 표준정규분포의 CDF를 의미합니다.

Proof. $μ \geq 0$ 일 때 $H_{0} : μ = 0 H_{1} : μ > 0$ 에 대한 가능도비는 $\exp (μ x - \frac{1}{2} μ^{2})$ 로 주어집니다. 즉, 이는 $x$ 에 대한 단조증가함수 이므로 검정의 기각역은 ${X > t}$ 꼴로 주어지고, 이는 네이만-피어슨 보조정리에 의해 최강력 검정입니다. 따라서 1종오류와 2종오류의 확률은 각각 다음과 같이 주어집니다.
$α (t) = Pr (X > t) = 1 - Φ (t), β (t) = Pr (X + μ \leq t) = Φ (t - μ)$
$α (t)$ 로부터 $t = Φ^{- 1} (1 - α)$ 이고, 따라서
$G_{μ} (α) = β (α) = Φ (Φ^{- 1} (1 - α) - μ)$
가 성립합니다.

DefinitionPermalink

Randomized mechanism $M$ 이 임의의 이웃하는 데이터셋 $D \sim D^{'}$ 에 대해 다음을 만족하면 이를 $μ$ -GDP라고 정의합니다.

T (M (D), M (D^{'})) \geq G_{μ}

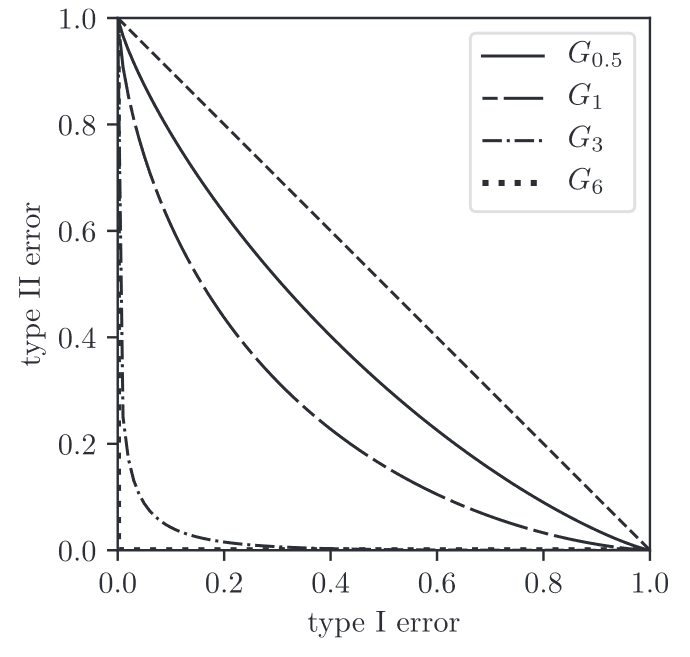$G_{μ}$ functions for different means

GDP의 장점은 우선 단일한 파라미터 $μ$ 하나로 정의된다는 것입니다. 위 그림과 같이, $μ$ 값을 조정하는 것 만으로 indistinguishability를 확인할 수 있습니다. $μ$ 값이 낮은 경우( $μ = 0.5$ ) 어느 정도의 프라이버시를 보장한다고 말할 수 있습니다.

GDP and Gaussian mechanismPermalink

Gaussian mechanism을 적용하면 $μ$ -GDP를 만족시킬 수 있습니다. 구체적으로는, 다음과 같습니다.

Gaussian mechanism $M (D) = θ (D) + Z, Z \sim (0, Δ^{2} / μ^{2})$ 는 $μ$ -GDP를 만족시킨다.

여기서 $θ (D)$ 는 단변량 통계량을 의미하고 $Δ$ 는 L1 sensitivity를 의미합니다.

PropertiesPermalink

Post-processingPermalink

만일 randomized mechanism $M$ 이 $f$ -DP라면, post-processing $Proc \circ M$ 역시 $f$ -DP를 만족한다는 특징이 있습니다. 여기서 post-processing $Proc$ 은 $M$ 의 출력값 $M (D) \in Y$ 을 어떤 공간 $Z$ 로 매핑하는 함수를 의미합니다.

Group privacyPermalink

데이터셋 $D, D^{'}$ 가 존재하여,

D = D_{0} \sim D_{1} \sim \dots \sim D_{k} = D^{'}

을 만족할 때, $D, D^{'}$ 를 k-neighbours^k-이웃이라고 정의합니다. 즉, $D, D^{'}$ 의 Hamming distance가 $k$ 이하인 데이터셋의 관계를 의미합니다. 이에 대해, randomized mechanism $M$ 이 크기 $k$ 인 그룹들에 대해 $f$ -DP를 만족한다는 것은 모든 $k$ -이웃인 $D, D^{'}$ 에 대해

T (M (D), M (D^{'})) \geq f

를 만족하는 것으로 정의됩니다.

이에 관하여 다음의 정리가 성립합니다.

$f$ -DP인 메커니즘 $M$ 은 크기 $k$ 인 그룹들에 대해 $[1 - (1 - f)^{\circ k}]$ -DP를 만족한다.

여기서 $f^{\circ k} = (f \circ f \circ \dots \circ f)$ 은 $k$ 번 합성된 trade-off function을 의미합니다 (정의역과 치역이 $[0, 1]$ 이므로 가능함). 또한, GDP에 대해서 위 정리는 다음과 같이 간단한 형태로 주어집니다.

$μ$ -GDP인 메커니즘 $M$ 은 크기 $k$ 인 그룹들에 대해 $k μ$ -GDP를 만족한다.

직관적으로 생각해보면, 그룹의 크기가 커질수록 그룹 내의 차이를 감지하는 것이 쉬워지기 때문에 이러한 현상이 발생하는 것으로 보입니다.

ReferencesPermalink

Dong, J., Roth, A., & Su, W. J. (2022). Gaussian Differential Privacy. Journal of the Royal Statistical Society Series B: Statistical Methodology, 84(1), 3–37. https://doi.org/10.1111/rssb.12454