Gaussian Process and Deep Neural Networks

Gaussian Process and Neural Networks

신경망 구조는 일반적으로 Universal Approximation Theorem에 의해 비선형 함수를 근사하는데 효과적으로 이용된다. 이러한 특성을 이용하면, 다음과 같이 신경망의 구조적 특징과 가우시안 프로세스의 비모수적 유연성^{nonparametric flexibility}을 결합한 커널을 구성할 수도 있다.

\[\mathcal{K}_{\theta}(x,x') = \exp \left(- \frac{1}{2\sigma^{2}} \Vert h_{\theta}(x) - h_{\theta}(x')\Vert^{2}\right)\]

여기서 $h_{\theta}(x)$는 $\theta$로 모수화되는 심층신경망을 의미한다. 이러한 커널을 가우시안 프로세스에 도입하면, $\theta$에 대한 marginal likelihood를 최대화하는 방향으로 모수를 학습할 수 있다.

실제로 Deep MLP kernel을 이용하면 아래 그림과 같이 불연속적인 함수를 학습하는데 효과적이다.

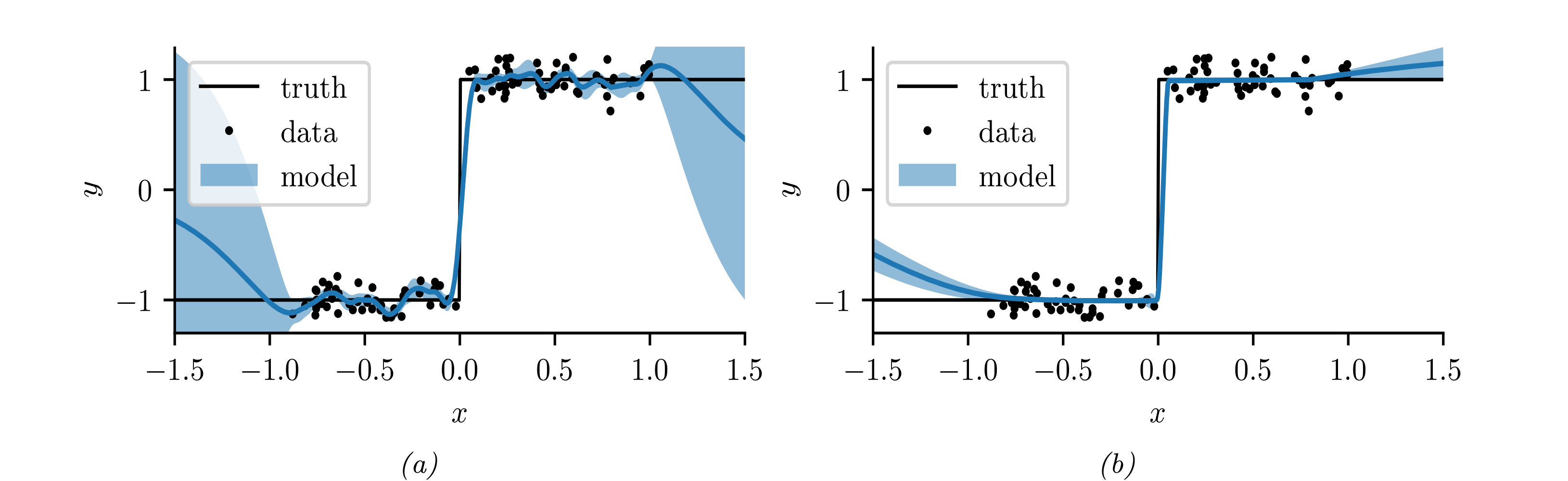
위 그림에서 $(a)$는 Matern covariance function, $(b)$는 Deep MLP kernel을 사용한 결과이다. 일반적인 커널함수를 사용할 경우 예측치가 주어지지 않는 구간 $(1.0,\infty),(-\infty,-1.0)$ 에 대해 예측 분산이 높게 구해지지만, 입력 데이터에 간단한 심층신경망을 부과하는 것 만으로도 out-of-sample prediction의 분산을 크게 줄일 수 있다.

NN-GP

다음과 같은 심층신경망 모델을 생각하자.

\[f_{k}(x) = b_{k} + \sum_{j=1}^{H}v_{jk}h_{j}(x) , \quad h_{j}(x)=\varphi(u_{0j}+ x^{\top}u_{j})\]

여기서 $H$는 hidden unit의 개수이고, $\varphi$는 비선형 활성함수(e.g. ReLU)를 나타낸다. 일반적인 신경망 모델과는 다르게, 이제 위 모델의 파라미터들에 대해 가우시안 사전분포를 다음과 같이 부여하는 상황을 생각해보자.

\[b_{k}\sim \mathcal{N}(0,\sigma_{b}),\;v_{jk}\sim \mathcal{N}(0,\sigma_{v}),\; u_{j}\sim \mathcal{N}(0,\Sigma)\]

이 경우 사전분포로부터 \(\mathrm{E}_{\theta}f_{k}(x)=0\) 임은 쉽게 유추가능하다. 공분산의 경우 다음과 같이 계산이 가능하다.

\[\begin{align} \mathrm{E}_{\theta}[f_{k}(x)f_{k}(x')] &= \mathrm{E}_{\theta}\left[ \left(b_{k}+\sum_{j=1}^{H}v_{jk}h_{j}(x)\right)\left(b_{k}+\sum_{j=1}^{H}v_{jk}h_{j}(x')\right)\right]\\ &= \sigma^{2}_{b}+\sum_{j=1}^{H}\mathrm{E}_{\theta}v_{jk}^{2} \mathrm{E}_{u}[h_{j}(x)h_{j}(x')]\\ &= \sigma_{b}^{2}+ \sigma_{v}^{2}H \mathrm{E}_{u} [h_{j}(x)h_{j}(x')] \end{align}\]

이때, 사전분포를 주었으므로 각 레이어의 출력은 서로 독립인 확률변수들의 합으로 볼 수 있으므로, 우리는 중심극한정리^{Central Limit Theorem, CLT}를 활용할 수 있다. 따라서, $H\to \infty$인 경우를 생각해보자. 만일 $\sigma_{v}^{2}=\dfrac{\omega}{H}$ 으로 두면, 중심극한정리에 의해 출력층이 다음과 같이 정규분포로 분포수렴하게 된다.

\[f_{k}(x)\to\mathcal{N} \left(0, \sigma_{b}^{2}+\omega \mathrm{E}_{u}h(x)^{2}\right)\]

만일 $f_{k}(x_{1}),\cdots,f_{k}(x_{n})$ 에 대한 결합분포를 생각하면, 결합분포 역시 중심극한정리에 의해 다음과 같은 다변량 정규분포로 분포수렴한다.

\[\mathbf{f}_{k} \sim MVN \left(\mathbf{0}, \mathcal{K}(x,x')\right)\]

여기서 $\mathcal{K}(x,x’) = \sigma_{b}^{2}+ \omega \mathrm{E}_{u}[h(x)h(x’)]$ 으로 주어진다.

즉, 위 결과로부터 우리는 심층신경망의 각 레이어가 가우시안 프로세스로 수렴함을 확인할 수 있다. 커널함수를 계산하기 위해

\[\begin{align} \tilde x = (1,x),\quad \tilde u = (u_{0},u),\quad \tilde \Sigma &= \begin{pmatrix}\sigma_{0}^{2}& 0 \\ 0 & \Sigma\end{pmatrix} \end{align}\]

으로 두면 다음과 같이 계산할 수 있다.

\[C(x,x') = \int h(\tilde u^{\top}\tilde x)h(\tilde u^{\top}\tilde x')\mathcal{N}(\tilde u\mid \mathbf{0},\tilde \Sigma)d\tilde u\]

이는 closed-form으로 계산될 수 있는데, ReLU 활성화함수에 대해서는 다음과 같이 주어진다.

\[\begin{align} C(\tilde x,\tilde x') &= \dfrac{f_{2}(\tilde x,\tilde x')}{\pi}\sin(\theta(\tilde x,\tilde x')) + \dfrac{\pi-\theta(\tilde x,\tilde x')}{\pi}\tilde x^{\top}\tilde \Sigma\tilde x'\\ f_{2}(\tilde x,\tilde x') &= \Vert \tilde \Sigma^{\frac{1}{2}}\tilde x\Vert\cdot \Vert\tilde \Sigma^{\frac{1}{2}}\tilde x'\Vert\\ \theta(\tilde x,\tilde x' ) &= \arccos \left(\sqrt{(\tilde x^{\top}\tilde \Sigma\tilde x)(\tilde x'^{\top}\tilde \Sigma\tilde x')}\right) \end{align}\]

이러한 형태로 주어지는 커널을 Neural Net Kernel^NN-kernel이라고도 한다.

Neural Tangent Kernel

일반적으로 신경망 학습은 역전파 과정(자동 미분)으로 그래디언트를 계산하여 stochastic gradient descnet 알고리즘을 수행한다. NN-kernel 에서는 각 파라미터들을 랜덤한 확률변수로 보고 사전분포를 주었지만, 실제로는 신경망의 학습 과정에서 그래디언트를 이용해 커널함수를 계산하는 방법을 생각하는 것이 더 바람직할 수 있다. 이를 해결하기 위한 방법이 Neural Tangent Kernel^NTK 이다.

SGD 알고리즘에서 $t$번째 step의 업데이트를 다음과 같이 작성하자.

\[\partial_{t}\theta_{t} = -\eta\nabla_{\theta}\mathcal{L}(f_{t}) = -\eta\nabla_{\theta}f_{t}\cdot \nabla_{f} \mathcal{L}(f_{t})\]

이때 다음과 같이 tangent kernel matrix $\mathcal{T}$ 를 정의하면

\[\mathcal{T}_{t}(x,x'):= \nabla_{\theta}f_{t}(x) \cdot \nabla_{\theta}f_{t}(x') = \sum_{p=1}^{P}\dfrac{\partial f(x:\theta)}{\partial \theta_{p}}\bigg\vert_{\theta_{t}}\dfrac{\partial f(x':\theta)}{\partial \theta_{p}}\bigg\vert_{\theta_{t}}\]

다음과 같이 함수에 대한 그래디언트를 나타낼 수 있다.

\[\partial_{t}f_{t}=\nabla_{\theta}f_{t}^{\top}\partial_{t}\theta_{t}=-\eta\mathcal{T}_{t}\cdot \nabla_{f}\mathcal{L}(f_{t})\]

만일 learning rate $\eta\to 0$ 이고, width $P\to\infty$ 인 경우를 생각하면, 위 tangent kernel matrix는 아래와 같은 constant matrix로 수렴한다. 이를 NTK라고 정의한다.

\[\mathcal{T}(x,x') \overset{\triangle}{=} \nabla_{\theta}f(x:\theta_{\infty})\cdot \nabla_{\theta}f(x':\theta_{\infty})\]

NTK는 합성곱 신경망, 그래프 신경망 등 다양한 모델에 활용된다.

Deep Gaussian Process

신경망을 커널로 구성하는 방법 대신, 가우시안 프로세스 여러개를 신경망처럼 구성하는 방법 역시 고려해볼 수 있다. 이러한 방법을 Deep Gaussian Process, DGP라고 하며 이는 가우시안 프로세스 사전분포를 갖는 함수들의 합성으로 정의된다. $L$개의 레이어를 갖는 DGP는 다음과 같이 정의된다.

\[\mathrm{DGP}(x) = \mathbf{f}_{L}\circ \cdots\circ \mathbf{f}_{1}(x),\quad \mathbf{f}_{i}(\cdot) = (f_{i}^{(1)}(\cdot),\ldots,f_{i}^{(H_{i})}(\cdot)), \quad f_{i}^{(j)}\sim \mathrm{GP}(0,\mathcal{K}_{i}(\cdot,\cdot))\]

사실 일반적인 single layer GP도 비모수적인 방법으로 어떤 함수든 모델링할 수 있다. 그래서 레이어를 여러개 쌓는 DGP가 크게 유용해보이지는 않을 수 있지만, 좀 더 general한 분포를 고려할 수 있다는 것이 알려져 있다.

References

• Murphy, K. P. (2023). Probabilistic machine learning: Advanced topics. The MIT Press.
• Rasmussen, C. E., & Williams, C. K. I. (2006). Gaussian processes for machine learning. MIT Press.