Hidden Markov Model

은닉 마코프 모형^{Hidden Markov Model, HMM} 이란 message passing algorithm(or belief propagation algorithm)의 일종이다. 여기서 message passing이란, 그래프 구조에서 각 노드가 다음 노드로 정보를 전달하며 어떤 결론을 도출하는 과정을 의미하는데, 전달되는 정보는 확률분포 형태를 가진다. 이러한 모델링으로 초기 상태를 예측하거나, 전이 확률 등을 계산하는 모델 중 하나가 은닉 마코프 모형이다.

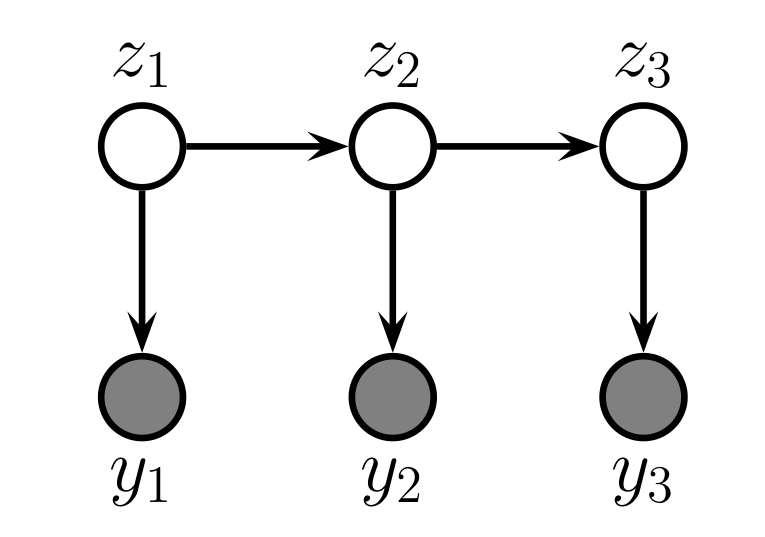
위 그림은 간단한 형태의 HMM을 나타낸다. 상태가 전이되는(정보 전달이 이루어지는) 은닉 노드 $z_1,z_2,z_3$ 가 존재하며, 각 은닉 노드에는 해당 노드의 정보를 바탕으로 결정이 이루어지는 관측가능한 노드 $y_1,y_2,y_3$가 대응하여 존재한다. 이러한 구조를 상태공간 모형^{state space model}이라고도 한다. HMM의 확률분포는 다음과 같이 나타낼 수 있다.

\[p(\mathbf{y}_{1:T},\mathbf{z}_{1:T})=\bigg[p(z_{1})\prod_{t=2}^{T}p(z_{t}\vert z_{t-1})\bigg]\bigg[\prod_{t=1}^{T}p(y_{t}\vert z_{t})\bigg]\]

이는 HMM 모형이 Bayesian network에 해당하기 때문에 BN의 성질로부터 얻어진다.

Inference

HMM에서 주된 관심사 중 하나는 각 은닉 노드들의 분포를 찾는 것이다. 즉, 관측가능한 노드들이 주어졌을 때 다음 사후분포를 계산하는 것이다.

\[p(z_{t}=j\vert \mathbf{y}_{t+1:T},\mathbf{y}_{1:t}) \propto p(z_{t}=j,\mathbf{y}_{t+1:T}\vert \mathbf{y}_{1:t})p(z_{t}=j\vert \mathbf{y}_{1:t})p(\mathbf{y}_{t+1:T}\vert z_{t}=j)\]

이때, 세번째 항은 Markov 성질로부터 얻어진다. 계산 순서는 다음과 같다. 우선 filtering distribution이라고도 하는 두번째 항 $p(z_{t}=j\vert \mathbf{y}_{1:t})$ 를 계산한다. 이는 시간순으로 계산할 수 있다(forward). 이후 세번째 항 $p(\mathbf{y}_{t+1:T}\vert z_{t}=j)$ 을 계산하는데, 이는 시간의 역순으로 이루어진다(backward). 구체적인 알고리즘은 아래와 같다.

Forwards-backwards algorithm

Forward pass

Forwards-backwards(FB) 알고리즘은 HMM 추론에서 가장 일반적인 접근 방식이다. HMM에서 각 시점의 은닉 상태는 이산형 확률변수로 나타낼 수 있으므로 belief state $p(z_{t}\vert \mathbf{y}_{1:t})$는 벡터로 표현가능하다. 이때 벡터의 $j$번째 성분을 $\alpha_{t}(j):=p(z_{t}=j\vert \mathbf{y}_{1:t})$ 로 표현하자. 마찬가지로, local evidence($t$ 시점에서 잠재변수가 주어질 때 관측변수의 조건부 확률) 역시 벡터로 표현가능하다. 이를 $\lambda_{t}(j):= p(y_{t}\vert z_{t}=j)$ 라고 나타내자. 또한, 전이행렬 $A_{i,j}$ 를 $p(z_{t}=j\vert z_{t-1}=i)$ 로 정의하면, predict step은 다음과 같다.

\[\begin{align} \alpha_{t\vert t-1}(j) &:= p(z_{t}=j\vert \mathbf{y}_{1:t-1}) \\ &= \sum_{i}p(z_{t}=j\vert z_{t-1}=i)p(z_{t-1}=i \vert \mathbf{y}_{1:t-1})\\ &= \sum_{i}A_{i,j}\alpha_{t-1}(i) \end{align}\]

그리고 $\alpha_{t}$ 에 대한 업데이트는 아래와 같이 이루어진다.

\[\begin{align} \alpha_{t}(j) &= \frac{1}{Z_{t}}p(y_{t}\vert z_{t}=j)p(z_{t}=j\vert\mathbf{y}_{1:t-1})\\ &= \frac{1}{Z_{t}}\lambda_{t}(j)\alpha_{t\vert t-1}(j) \end{align}\]

여기서 $Z_{t}$는 정규화를 위한 상수이다. 이는 $Z_{t}=\sum_{j=1}^{K}\lambda_{t}(j)\alpha_{t\vert t-1}(j)$로 정의된다.

Backward pass

역방향 과정에서는 조건부 가능도

\[\beta_{t}(j):= p(\mathbf{y}_{t+1:T}\vert z_{t}=j)\]

를 구하는 것이 목적이 된다. $\beta$는 재귀적인 과정으로 구할 수 있는데, 과정은 아래와 같다.

\[\begin{align} \beta_{t-1}(i) &= p(\mathbf{y}_{t:T}\vert z_{t-1}=i)\\ &= \sum_{j}p(z_{t}=j,y_{t},y_{t+1:T}\vert z_{t-1}=i)\\ &= \sum_{j}p(\mathbf{y}_{t+1:T}\vert z_{t}=j,y_{t},z_{t-1}=i)p(z_{t}=j, y_{t}\vert z_{t-1}=i )\\ &= \sum_{j}p(\mathbf{y}_{t+1:T}\vert z_{t}=j)p(z_{t}=j, y_{t}\vert z_{t-1}=i )\\ &= \sum_{j}p(\mathbf{y}_{t+1:T}\vert z_{t}=j)p(y_{t}\vert z_{t}=j, z_{t-1}=i)p(z_{t}=j\vert z_{t-1}=i )\\ &= \sum_{j}\beta_{t}(j)\lambda_{t}(j)A_{i,j} \end{align}\]

Combine

앞서 구한 두 벡터 $\alpha_{t},\beta_{t}$ 로부터 구하고자 하는 사후가능도를 다음과 같이 계산할 수 있다.

\[\gamma_{t}(j)=p(z_{t}=j\vert\mathbf{y}_{t+1:T},\mathbf{y}_{1:t}) \propto \alpha_{t}(j)\beta_{t}(j)\]

Viterbi Algorithm

은닉변수들의 사후가능도를 구하면, 이로부터 최대사후가능도 추정량의 시퀀스 $\mathbf{z}_{1:T}^{\star}$ 을 구할 수 있다.

\[\mathbf{z}_{1:T}^{\star}=\arg\max_{\mathbf{z}}p(\mathbf{z}_{1:T}\vert\mathbf{y}_{1:T})\]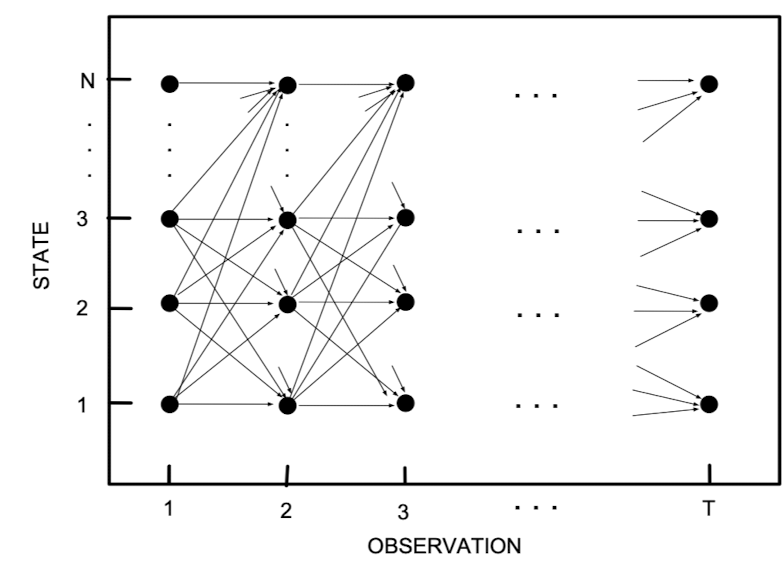

위 그림을 살펴보도록 하자. 이를 trellis diagram 이라고도 부르는데, 이는 각 시점에 대해 은닉노드의 상태 구성을 알려주는 그림이다. 그래프의 각 변에 대해 로그 (조건부)확률을 부여하면, 최대사후가능도 추정량 시퀀스를 찾는다는 것은 위 그림에서 전체 시점을 잇는 최단 경로를 찾는 문제가 된다. 이는 $O(TK^{2})$ 시간에 해결이 가능하며, Viterbi algorithm은 이를 해결하기 위한 알고리즘 중 하나이다.

Forwards pass

이전에 살펴본 정방향 계산에서

\[\alpha_{t}(j)=p(z_{t}=j,y_{1:t})=\sum_{z_{1},\cdots,z_{t-1}} p(z_{1:t-1},z_{t}=j,y_{1:t})\]

으로 정의하였는데 (정규화 상수는 생략), 여기서 합을 최대화함수로 대체하여 다음을 정의하자.

\[\delta_{t}(j):= \max_{z_{1},\cdots,z_{t-1}}p(z_{1:t-1},z_{t}=j,y_{1:t})\]

이는 시점 $t$의 은닉변수가 상태 $j$로 마무리되는 경로에 대한 확률이다. 그렇기에, 이는 시점 $t-1$의 은닉변수가 상태 $i$로 끝나는 경로와 $i$번째 상태에서 $j$번째 상태로의 전이를 포함한다. 그러므로 이를 다음과 같이 나타낼 수 있다.

\[\delta_{t}(j)=\lambda_{t}(j)\max_{i}\delta_{t-1}(i)A_{i,j}\]

이러한 관점에서, 이전 은닉변수(ancestor)의 최대가능 상태(most likely state)를 다음과 같이 정의할 수 있다.

\[a_{t}(j) := \arg\max_{i}\delta_{t-1}(i)A_{i,j}\]

Backwards pass

역방향 계산과정에서는, traceback 과정을 통해 가장 그럴듯한^probable 상태들의 시퀀스를 계산한다. 초기값은 $z_{T}^{\star}=\arg\max_{i}\delta_{T}(i)$ 를 이용하며, $z_{t}^{\star}=a_{t+1}(z_{t+1}^{\star})$ 로 계산이 이루어지게 된다. 만약 유일한 MAP 추정 시퀀스가 존재한다면, 이렇게 구한 시퀀스와 FB 과정으로 구한 시퀀스가 같게 된다.

Python Example

파이썬에서는 HMM 관련 패키지로 hmmlearn이 존재한다. hmmlearn 패키지에서는 아래와 같은 3가지 형태의 hmm을 제공한다.

HMM class	Description
GaussianHMM	HMM with Gaussian emissions.
GMMHMM	HMM with Gaussian mixture emissions.
CategoricalHMM	HMM with discrete emissions.

아래 예시를 이용하여 모형을 분석해보자.

Bob 은 그날의 날씨 (Rainy, Sunny) 에 따라 산책(Walk), 쇼핑(shop), 방청소(clean) 중 하나의 행동을 취한다. Alice 는 Bob 이 그날그날 어떠한 행동을 취했는지만을 알고 있으며, 이를 통해 날씨에 대해 추측을 하고자 한다. 이를 Hidden Markov chain 의 관점에서 보면 날씨 (Rainy, Sunny)는 숨겨진 정보로써 은닉변수에 해당하며, Bob이 취하는 행동은 각 날씨에서 특정 출력확률을 따라 관측되는 값으로 이해할 수 있다.

본 분석에서는 아래와 같은 형태의 Markov chain을 가정한다. 은닉변수의 초기상태에 대한 확률분포 $(0.6,0.4)$는 날씨의 경향에 대한 Alice의 믿음으로 이해할 수 있으며 전이확률과 출력확률은 아래와 같은 값을 갖는다고 하자.

\[\begin{align*} \pi &= (0.6,0.4) \\ A &= \begin{pmatrix} 0.7 & 0.3 \\ 0.4 & 0.6 \end{pmatrix} \\ B &= \begin{pmatrix} 0.1 & 0.4 & 0.5 \\ 0.7 & 0.2 & 0.1 \end{pmatrix} \end{align*}\]

예를 들어, 전날에 비(Rainy)가 왔다면 다음날 날씨가 맑을(Sunny) 확률은 0.3이며 맑은 날씨에 Bob이 쇼핑을 할 확률은 0.3 이라고 생각할 수 있다.

이제 hmmlearn 내의 CategoricalHMM 를 이용하여 실제 모형을 만들고 그로부터 관측값을 얻어보자.

import numpy as np
from hmmlearn import hmm
import random


states = ('Rainy', 'Sunny') # 은닉변수
n_states = len(states)
observations = ('walk', 'shop', 'clean') # 관측변수
 
# 실제 모형
model_true = hmm.CategoricalHMM(n_components=n_states, init_params = '', params='')# n_components : 은닉변수가 가질 수 있는 값의 개수

# 은닉변수의 초기상태에 대한 확률분포
model_true.startprob_ = np.array([0.6, 0.4])
 
# 전이확률 행렬
model_true.transmat_ = np.array([
  [0.7, 0.3],
  [0.4, 0.6]
])

# 출력확률 행렬
model_true.emissionprob_ = np.array([
  [0.1, 0.4, 0.5],
  [0.6, 0.3, 0.1]
])

np.random.seed(100)
bob_says, hidden_state = model_true.sample(10) # 크기 10 인 관측값을 랜덤하게 출력
print(bob_says.T)
print("Bob says:", ", ".join(map(lambda x: observations[int(x)], bob_says)))
print("Hidden state:", ", ".join(map(lambda x: states[int(x)], hidden_state)))

학습(Learning) 과 디코딩(Decoding)

hmmlearn 패키지에서는 fit 함수를 이용하여 HMM의 모수 (전이확률($A$), 출력확률($B$), 은닉변수의 초기상태에 대한 확률($\pi$)) 를 추정할 수 있으며, decode 함수를 이용하여 최적의 은닉변수열을 찾을 수 있다.

model_pred = hmm.CategoricalHMM(n_components=n_states, n_iter = 100, tol = 1.0e-2)
model_pred = model_pred.fit(bob_says) # 추정된 모형

추정된 모수들은 각각 아래와 같다.

# 전이확률 행렬
print("Transition matrix")
print(model_pred.transmat_.round(3))

# 출력확률 행렬
print("Emission matrix")
print(model_pred.emissionprob_.round(3))

# 은닉변수의 초기상태에 대한 확률분포
print("Initial state distribution")
print(model_pred.startprob_.round(3))

# Transition matrix [[0.998 0.002] [1. 0. ]] 
# Emission matrix [[0.334 0.221 0.445] [0. 1. 0. ]] 
# Initial state distribution [0. 1.]

decode 함수를 이용하면, Viterbi 알고리즘을 이용해 앞서 얻은 관측값 bob_says 에 대한 최적의 은닉변수열을 구할 수 있다.

logprob, hidden_state_pred = model_pred.decode(bob_says, algorithm="viterbi")

print("Bob says:", ", ".join(map(lambda x: observations[int(x)], bob_says)))
print("Prediction of hidden state:", ", ".join(map(lambda x: states[int(x)], hidden_state_pred)))
print("Accuracy:",np.mean(hidden_state==hidden_state_pred)) # 실제 날씨와 일치하는 비율

# Bob says: shop, clean, shop, clean, clean, walk, shop, clean, walk, walk
# Prediction of hidden state: Sunny, Rainy, Rainy, Rainy, Rainy, Rainy, Rainy, Rainy, Rainy, Rainy
# Accuracy: 0.6

References

Murphy, K. P. (2023). Probabilistic machine learning: Advanced topics. The MIT Press.