최근 딥러닝 관련 연구동향을 살펴보던 중, 일반적으로 널리 사용되던 MLPMulti-Layer Perceptron를 대체할 수 있는 모델이 등장했다는 소식을 접했습니다. KANKolmogorov-Arnold Network가 바로 그것인데 (Liu et al., 2024), 아직 저널이나 컨퍼런스에 발표되지는 않은 논문이지만 큰 화제를 모으고 있기도 합니다. 이번 글에서는 KAN의 이론적인 원리를 살펴보고 이를 python으로 구현해놓은 패키지(pykan)가 있어 이에 대해서도 간략히 살펴보도록 하겠습니다.

Introduction

MLP는 현재 딥러닝이라고 불리는 학습 이론들의 근간이 되는 모델입니다. 가중치 행렬 $W$를 사용한 선형결합과 비선형 활성함수 (ex. ReLU)를 이용해 임의의 비선형 함수를 근사합니다. 이는 Universal approximation theorem으로 설명되는데, 이는 임의의 비선형함수를 주어진 오차 내에서 몇개의 레이어와 몇개의 깊이(depth)를 갖는 완전연결 네트워크(fully-connected network, FCN)으로 근사할 수 있음을 의미합니다.

반면, KAN의 경우 Kolmogorov-Arnold representation theorem을 근간으로 모델을 전개합니다. 무언가 거창한 정리와 모델로 보일 수는 있지만, 저자는 KAN이 nothing more than combinations of splines and MLP, 즉 spline 모델과 MLP를 결합시킨 것에 불과하다고 합니다.

KAN은 MLP에 대응하는 모델이기 때문에, 현재 CVComputer Vision, NLPNatural Language Processing 등 다양한 분야에서 사용되는 CNN, Tranformer 등의 모델을 대체할 수 있는지에 대해서는 알려지지 않았습니다. 따라서 이 논문에서는 구체적인 활용 분야로 과학 분야에서의 활용을 제안하고 있습니다.

KAN

Kolmogorov-Arnold Representation Theorem

Kolmogorov-Arnold representation theorem (이하 KRT)는 다음과 같이 주어집니다.

(Multivariate) Smooth function $f:[0,1]^{n}\to \mathbb{R}$ 는 다음과 같이 나타낼 수 있다.

\[f(\mathbf{x}) = f(x_{1},\ldots,x_{n}) = \sum_{q=1}^{2n+1}\Phi_{q}\left(\sum_{p=1}^{n}\phi_{q,p}(x_{p})\right) \tag{KRT}\]

여기서 $\phi_{q,p}:[0,1]\to \mathbb{R}$ 이고 $\Phi_{q}:\mathbb{R}\to \mathbb{R}$ 이다.

위 정리의 의미를 생각해보자면, $n$차원 다변량 함수를 $n$개의 단변량 함수 $\phi$들의 합으로 나타낼 수 있다는 것입니다. 머신러닝 관점에서 생각해보자면, 이는 고차원 함수를 학습하고자 할 때 $n$개의 단변량 함수를 학습하는 것으로 귀결되고, 차원의 저주curse of dimensionality를 피할 수 있다고 기대할 수 있습니다.

KAN architecture

MLP vs KAN

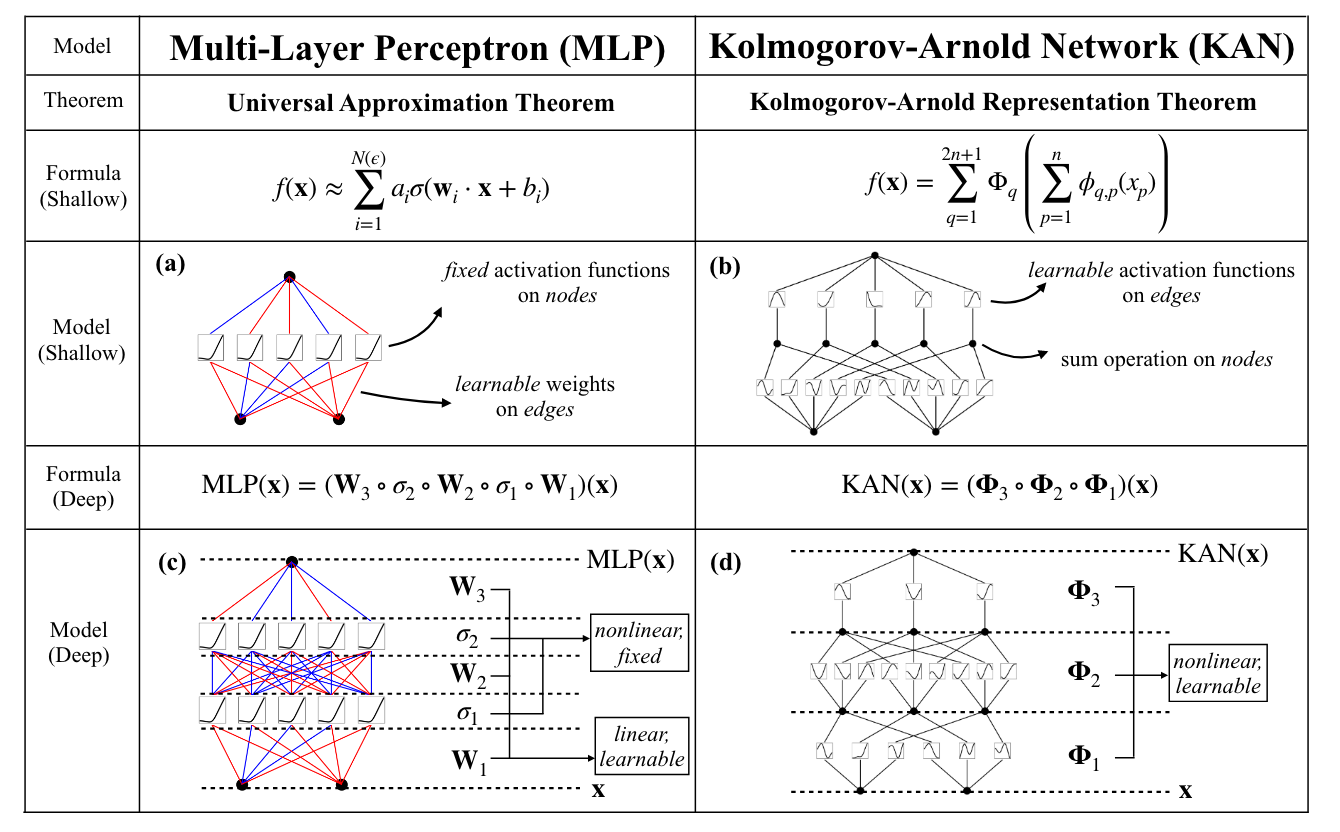MLP와 KAN을 비교한 도표 (Liu et al., 2024)

위 표는 MLP와 KAN을 비교한 표입니다. MLP를 그래프 구조로 표현하면 왼쪽의 (a)와 같이 각 노드에 활성함수를 대응시키고, 각 엣지에 가중치 행렬 $W$ 들을 대응시킬 수 있을 것입니다. 반면, 아래 설명할 KAN의 경우는 각 노드가 함수값에 대응되고, 각 엣지에는 함수 $\phi,\Phi$ 들이 대응됩니다. 또한, 가중치를 학습하는 MLP와 달리 함수들을 학습시킨다는 차이점이 있습니다. 자세한 구조는 다음과 같습니다.

Simple KAN

우선, 입력 데이터 \(\mathbf{x}_{0}=\lbrace x_{0,1},x_{0,2}\rbrace\)가 2차원으로 주어진다고 가정하면, 식 $(\mathrm{KRT})$ 는 다음과 같습니다.

\[x_{2,1}=\sum_{q=1}^{5}\Phi_{q}\left(\phi_{q,1}(x_{0, 1}) + \phi_{q,2} (x_{0, 2})\right) \tag{1}\]

이 경우 KAN의 computation graph는 다음과 같이 주어집니다.

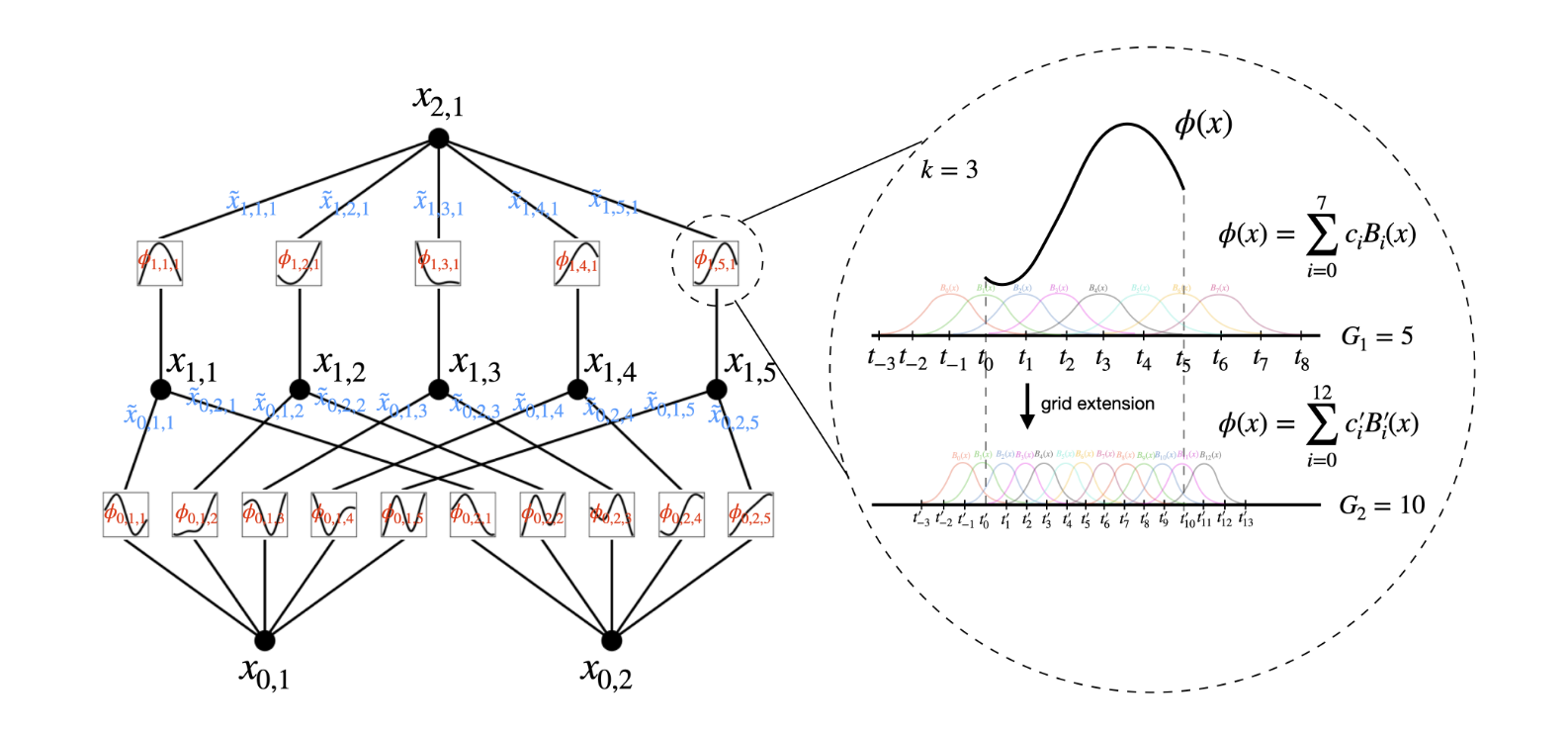Computation graph of $n=2$ KAN (Liu et al., 2024)

우선, 그래프의 각 노드 (검은색 정점)은 단변량의 함수값 혹은 데이터에 대응됩니다. 입력 데이터의 각 성분 $x_{0,1},x_{0,2}$ 가 계산 그래프의 아래 첫번째 노드들로 주어집니다. 이후 식 $(1)$에서 확인할 수 있듯이 각 성분에는 $\phi_{q,1}:q=1,\ldots,5$ 가 대응되기 때문에, $x_{0,1},x_{0,2}$에서 각각 5개의 엣지가 나가는 것을 확인할 수 있습니다 (그래프의 $\phi_{0,1,1}\ldots\phi_{0,2,5}$). 이후, 이들이 합해질 때에는 (식에서 덧셈 부분) $q$ 값이 동일한 함수값들끼리 더해지기 때문에 $\phi_{0,1,1}+\phi_{0,2,1} \ldots$ 끼리 각각 더해집니다. 이로부터 $x_{1,1},\ldots x_{1,5}$의 5개 성분을 갖는 hidden layer가 구성됩니다. 마지막으로, $\sum_{q}\Phi_{q}$ 부분의 연산이 이루어지기 위해 각각의 은닉층 성분에 함수값들을 더하고, 이것이 output $x_{2,1}$으로 구성됩니다. (위 그림에서는 표기의 통일성을 위해 $\phi,\Phi$를 구분하지 않고 $\phi$로 나타낸 것 같습니다.)

식 $(\mathrm{KRT})$ 는 2-layer-KAN에 대응됩니다.

또한, 각각의 함수 $\phi_{q,p},\Phi$ 들은 학습이 가능해야 하므로 spline을 이용하여, 각 함수들의 계수(coefficient)를 학습합니다. KAN 에서는 B-spline을 이용합니다. (ex. Spline 포스트의 natural cubic spline 참고)

KAN Layer

앞서 살펴본 KAN의 구조는 단일한 KRT에 대응되는 것으로, $2n+1$개의 너비를 갖는 hidden layer가 사용되었습니다. 그런데, MLP에 비하면 이는 매우 얕고 단순한 구조로 볼 수 있습니다. 따라서 이를 확장가능하게 만들어야 하는데, 이를 위해서는 우선 1개의 KAN layer가 무엇을 의미하는지에 대해 정의가 필요합니다.

입력 벡터가 $N$차원이고 출력 벡터가 $M$차원인 KAN layer는 다음과 같이 1차원 함수 $\phi_{q,p}$로 구성된 행렬로 정의할 수 있습니다.

\[\Phi=\lbrace \phi_{q,p}\rbrace ,\quad p=1,2,\cdots,N,\quad q=1,2,\cdots,M\]

따라서 위에서 살펴본 KRT에 대응하는 네트워크 구조는 $2\to5\to1$ 차원으로 순차적으로 변환되므로, 2개의 KAN layer로 구성된다고 할 수 있습니다. 이를 논문에서는 $[n,2n+1,1]$-KAN 으로 표현하기도 합니다. 또한, 이를 바탕으로 KAN layer를 순차적으로 쌓는 것으로부터 Deep KAN을 구성할 수 있게 됩니다.

\[\begin{align} \mathrm{KAN}(\mathbf{x}) &= \left(\Phi_{L-1}\circ \Phi_{L-2}\circ\cdots\circ\Phi_{1}\circ\Phi_{0}\right)(\mathbf{x})\\ &= \sum_{i_{L-1}=1}^{n_{L-1}}\phi_{L-1,i_{L},i_{L-1}}\left(\sum_{i_{L-2}=1}^{n_{L-2}}\cdots \left(\sum_{i_{1}=1}^{n_{1}}\phi_{1,i_{2},i_{1}}\left(\sum_{i_{0}=1}^{n_{0}}\phi_{0,i_{1},i_{0}}(x_{i_{0}})\right)\right)\cdots\right) \end{align}\]

Activation function

앞서 activation function $\phi$ 들을 학습가능하게끔 하기 위해 $B$-spline을 이용한다고 하였는데, KAN에서는 구체적으로 이를 다음과 같이 설정합니다.

  1. Residual activation functions

    \[\phi(x) = w(b(x) + \mathrm{spline}(x)).\]

    여기서 $b(x)$는 basis function 이라고 부르며 (spline basis와 다름에 유의), 일종의 residual connection 역할을 수행합니다. 다음과 같이 silu function으로 주어집니다.

    \[b(x) = \mathrm{silu}(x) = \frac{x}{1+e^{-x}}\]

    Spline의 경우 다음과 같이 $B$-spline의 선형결합으로 주어집니다.

    \[\mathrm{spline}(x) = \sum_{i}c_{i}B_{i}(x)\]

    $w$는 activation function의 출력값의 스케일을 조절하기 위해 사용되는 factor입니다.

  2. Initialization

    각 scale $w$는 Xavier initialization으로 초기화하며, 각 activation function $\phi$는 $\mathrm{spline}(x)\approx 0$ 이 되도록 초기화합니다. 이는 각 계수 $c_{i}$들을 $N(0,\sigma^{2})$ 로부터 샘플링하는 것으로 수행합니다. (KAN에서는 $\sigma=0.1$ 을 사용합니다.)

    \[\text{Initialize } c_{i} \overset{\mathrm{iid}}{\sim} N(0,\sigma^{2})\]

  3. Spline grid update 각 spline의 격자점(grid)을 업데이트하여, 활성함수의 함수값이 학습 중 고정된 범위를 넘어서는 것을 방지합니다.

이러한 방식으로 정의되는 KAN은 총

\[O(N^{2}L(G+k)) \sim O(N^{2}LG)\]

개의 parameter를 갖게 됩니다. 여기서 $L$은 레이어 개수(depth), $N$은 각 레이어의 너비(width), $k,G$는 각각 spline의 차수와 구간의 수(격자점 개수 - 1)을 의미합니다. 일반적으로 MLP가 $O(N^{2}L)$ 개의 parameter 수를 갖는 것에 비하면 더 많은 parameter를 갖는 것 처럼 보이지만, 실제로는 KAN이 요구하는 $N$의 수가 훨씬 적습니다.

KAT

4개의 변수를 갖는 함수

\[f(x_{1},x_{2},x_{3},x_{4}) = \exp(\sin(x_{1}^{2}+x_{2}^{2})+\sin(x_{3}^{2}+ x_{4}^ {2}))\]

는 3개의 레이어를 갖는 $[4,2,1,1]$ KAN으로 나타낼 수 있습니다. 이 경우 각 레이어는 $x^{2},\sin(x), \exp(x)$ 로 계산됩니다. 반면, 이를 2-layer KAN으로 나타내면 activation function $\phi$를 smooth하게 구성할 수 없다는 문제가 있습니다. 이로부터 레이어를 깊게 설정하는 KAN이 smooth한 activation function을 갖게 해준다는 장점이 있고, 이와 관련하여 다음의 Approximation theorem이 존재합니다.

(KAT) 입력 데이터 $\mathbf{x}\in \mathbb{R}^{n}$ 에 대해 함수 $f(\mathbf{x})$ 가 다음과 같이 KAN으로 표현된다고 하자.

\[f=(\Phi_{L-1}\circ\cdots\circ\Phi_{0})\mathbf{x}\]

그러면 상수 $C$가 존재하여 다음의 approximation bound가 성립한다.

\[\left\Vert f-(\Phi_{L-1}^{G}\circ\cdots\circ\Phi_{0}^{G})\mathbf{x}\right\Vert_{C^{m}} \le CG^{-k-1+m} \tag{KAT}\]

여기서 $G$는 $B$-spline에서 격자 크기(구간의 수)를, $k$는 smoothness order를 각각 의미하며 노음은 다음과 같이 정의한다.

\[\left\Vert g\right\Vert_{C^{m}} =\max_{\vert\beta\vert\le m} \sup_{x\in[0,1]^{n}}\left\vert D^{\beta}g(x)\right\vert\]

KAT의 핵심은 approximation bound가 입력 차원 N에 의존하지 않는다는 것입니다. 즉, spline의 가정 형태만 조절하면, 임의의 함수를 잘 근사할 수 있게 됩니다. 논문에서는 $k=3$, 즉 cubic spline을 사용하는 것이 적절하다고 제안한 반면, grid size $G$의 경우는 너무 fine하게 설정할 경우 test loss가 발산하는 overfitting 문제가 존재하는 것을 보였습니다. (아래) 만일 training data가 $n$개 있고, 전체 parameter 수가 $mG$개로 계산된다면, $G=\dfrac{n}{m}$ 을 넘지 않도록 설정하는 것이 적합하다고 합니다 (interpolation threshold).

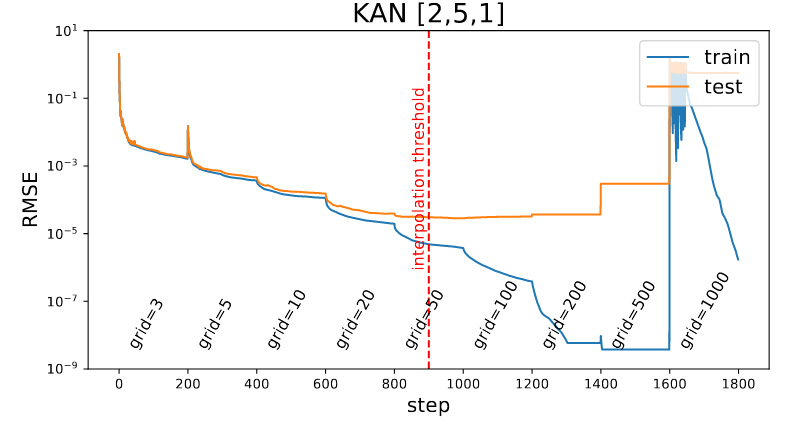[2,5,1] KAN의 loss graph

Symbolic regression

간단한 예시로, 2D input을 갖는 $f(x,y)=\exp(\sin(\pi x)+ {y^2})$로부터 생성된 데이터들이 있다고 가정해봅시다. 함수 $f$를 사전에 알고 있다면 이는 $[2,1,1]$-KAN으로 표현된다는 것을 알 수 있지만, 당면한 상황은 이를 모르는 상황입니다. 이 경우 충분히 큰 KAN을 먼저 가정한 후, sparsity regularization을 바탕으로 모델을 학습하여 불필요한 노드와 엣지를 제거하고 (prune), 이를 원래 함수로 나타냅니다. (아래 그림 참고)

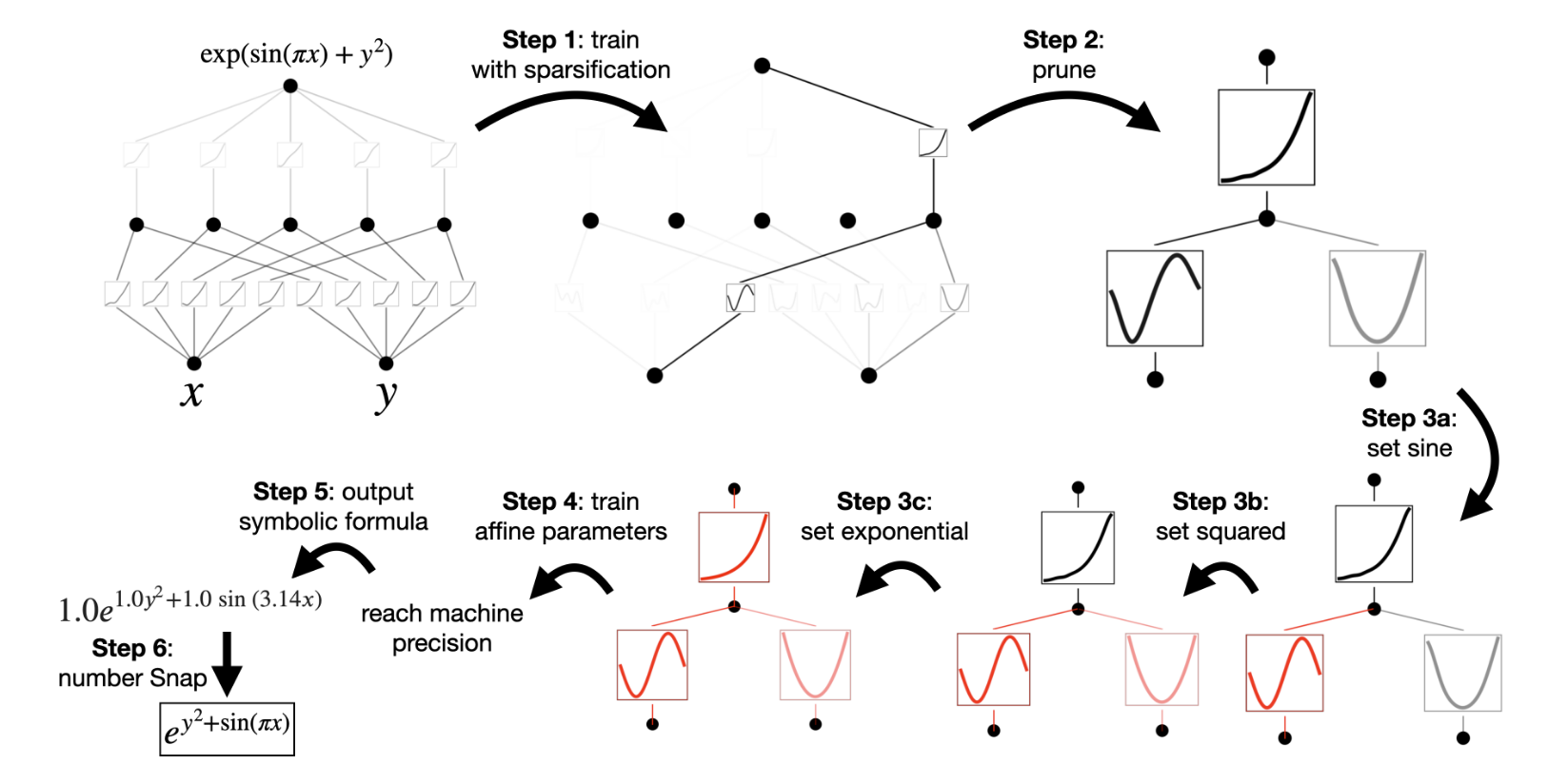
Sparsification

MLP에서는 regularization 기법을 이용해 가중치에 sparsity를 부여하였습니다. 이와 유사하게 KAN에서는 다음과 같이 레이어의 L1 노음을 정의합니다.

\[\left\vert \Phi\right\vert_{1}:=\sum_{i=1}^{n_\mathrm{in}}\sum_{j=1}^{n_\mathrm{out}}\left\vert \phi_{i,j}\right\vert_{1}\]

또한, 레이어의 엔트로피entropy를 다음과 같이 정의하여

\[S(\Phi) := \sum_{i=1}^{n_\mathrm{in}}\sum_{j=1}^{n_\mathrm{out}}\frac{\left\vert \phi_{i,j}\right\vert_{1}}{\left\vert \Phi\right\vert_{1}}\log \left(\frac{\left\vert \phi_{i,j}\right\vert_{1}}{\left\vert \Phi\right\vert_{1}}\right)\]

손실함수(목적함수)에 다음과 같이 regularization term을 추가합니다.

\[l_\mathrm{total} = l_\mathrm{pred} + \lambda \left(\mu_{1}\sum_{l=0}^{L-1}\left\vert \Phi_{l}\right\vert_{1}+ \mu_{2}\sum_{l=0}^{L-1}S(\Phi_{l})\right).\]

Prune

Sparsification으로 모델을 학습한 후, 각 $\phi$의 노음을 계산하여 이를 다음과 같은 incoming / outgoing score으로 정의합니다.

\[I_{l,i}=\max_{k}(\left\vert \phi_{l-1},k,i\right\vert_{1}),\quad O_{l,i}=\max_{j}(\left\vert \phi_{l+1},j,i\right\vert_{1})\]

만일 두 score가 정해진 threshold $\theta=0.01$을 넘는다면 해당 노드를 필요한 것으로 간주하고, 그렇지 않은 노드를 제거합니다. 이 과정으로부터 간단한 형태의 네트워크를 얻을 수 있습니다.

Symbolic functions

만일 일부 activation function이 로그함수, 지수함수와 같이 특정 함수로 표현가능하다면 $\phi$를 해당 함수의 아핀 변환affine transformation으로 고정할 수 있습니다. 이를 통해 파라미터 수를 줄일 수 있으며, 이후 해당 파라미터를 재학습하기 위해 모델을 재차 훈련합니다.

이러한 과정으로 모델을 학습하는 것을 symbolic regression이라고 하는데, 이는 위 예시처럼 간단한 함수의 학습에는 적용가능하지만 비교적 복잡한 함수에는 적용하기 어려운 문제가 있습니다. 위 symbolic regression은 KAN의 학습과정은 아니며, KAN의 학습은 함수공간에서 경사하강법을 사용하여 최적의 함수를 찾는 과정으로 이루어집니다. 다만 sparsification 등의 기법을 설명하기 위해 논문에 이러한 과정 역시 설명한 것으로 보입니다.

Pros

Accuracy

논문에서는 다양한 함수를 근사하는 문제에 MLP와 KAN을 사용하여 둘의 성능을 비교하였습니다. 실험을 통해 정확성(loss)과 모델 복잡성(parameter 수)에 대해 KAN이 더 나은 파레토 최적Pareto optimal을 달성하는 것을 보였습니다.

또한, KAN과 관련된 중요한 성질로 continual learning이 있습니다. 이는 하나의 문제를 해결하는 과정으로 모델이 학습된 이후, 다른 영역(domain)에서의 문제를 학습하는 것을 의미합니다. MLP 기반의 모델은 continual learning 문제에서 새로운 domain의 문제를 학습할 경우 이전의 풀이를 보존하지 못한다는 문제가 있습니다. 이는 activation function (ReLU, SiLU 등)의 globality에 의한 것으로 설명될 수 있습니다. (가중치의 업데이트가 $\mathbb{R}$ 전체에 영향을 미치기 때문)

반면 KAN은 새로운 단계의 문제를 해당 데이터의 영역에서만 해결하기 때문에 (locality), 이전 단계의 학습 결과를 비교적 잘 보존한다는 특징이 있습니다. (아래 그림 참고)

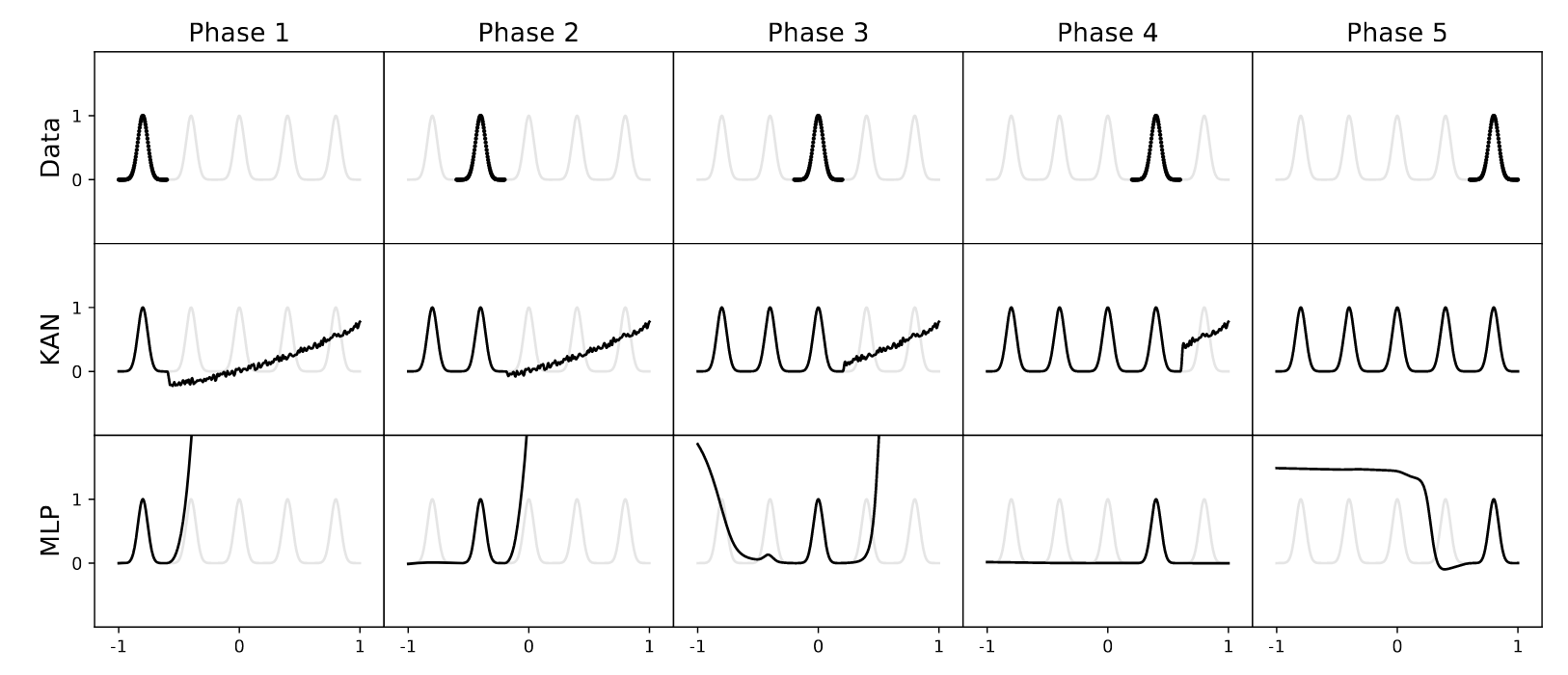MLP vs KAN : Continual Learning Task (Liu et al., 2024)

Interpretability

Symbolic regression에서 살펴본 것처럼, KAN은 학습된 함수를 해석하기 쉽다는 장점이 있습니다. 일부 연산자, 혹은 symbolic한 함수들은 KAN 구조로 쉽게 나타낼 수 있기 때문입니다 (아래 그림 참고).

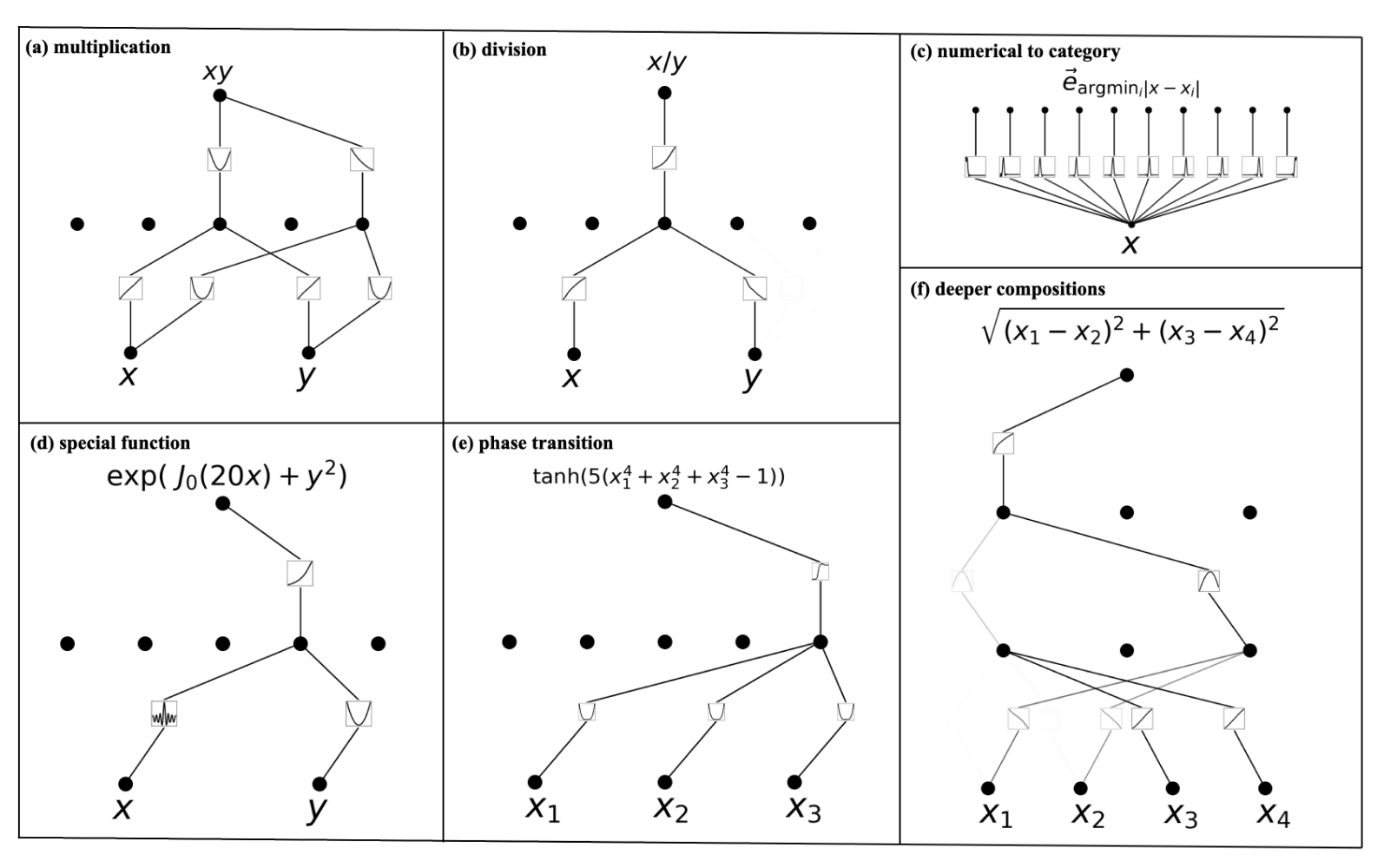Some symbolic tasks

Cons

위와 같은 장점에도 불구하고, KAN은 다음 몇 가지 단점들을 갖고 있습니다.

  1. Slow Training : 동일한 parameter 수를 갖는 MLP에 비해 10배 정도 느린 학습 속도
  2. Unable to batch training : KAN은 batch training이 불가능하며, 이는 학습 속도를 더욱 느리게 만듭니다. 이를 해결하기 위해 논문에서는 activation function들을 여러 그룹들로 묶어 각 그룹들에 동일한 function을 적용하는 방법을 제안합니다 (실제 사용 예시는 없음).

PyKAN

Python에서 KAN을 구현하기 위해 pykan 패키지를 이용해보도록 하겠습니다. pykan은 pytorch를 기반으로 구현되었으며, 다음과 같이 pip로 설치할 수 있습니다.

pip install pykan

공식 문서를 기반으로 간단한 함수추정 예시와 분류 문제를 다루어보도록 하겠습니다. 우선 필요한 라이브러리들은 다음과 같습니다.

import kan
import matplotlib.pyplot as plt
import numpy as np
import torch
from kan import KAN, create_dataset
from sklearn.datasets import make_classification, load_iris
from sklearn.model_selection import train_test_split

Symbolic regression

앞서 살펴본 간단한 이변량 함수

\[f(\mathbf{x}) = \exp(\sin(\pi x_{1})+x_{2}^{2})\]

를 추정하는 문제를 다루어보겠습니다. 우선 다음과 같이 torch.tensor 자료형을 갖는 데이터셋을 생성해줍시다.

f = lambda x: torch.exp(torch.sin(torch.pi*x[:,[0]]) + x[:,[1]]**2)

# Create dataset
torch.manual_seed(0)

X = torch.rand(1000, 2) * 2 - 1 # Random points in [-1, 1]^2
y = f(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
dataset = dict(train_input=X_train, train_label=y_train, test_input=X_test, test_label=y_test)

# Plot dataset
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(dataset['train_input'][:, 0], dataset['train_input'][:, 1], dataset['train_label'], c='c', marker='o')
plt.show()

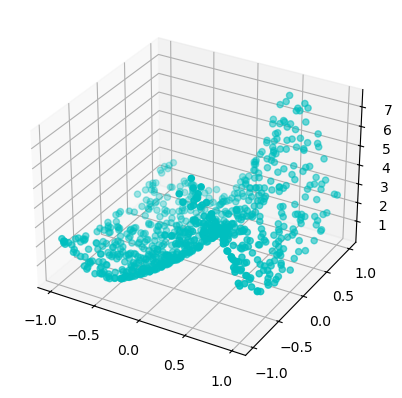Sample dataset

KAT에서 다룬 것 처럼 우선 $[2,5,1]$-KAN으로 해당 함수를 근사해보도록 하겠습니다. width 인자를 주어

# Create KAN
model = KAN(width=[2,5,1], grid=3, k=3, seed=0)

# Plot
model(dataset['train_input'])
model.plot(beta=100, in_vars=['$x_1$', '$x_2$'], out_vars=['y']) # beta controls the transparency of the plot

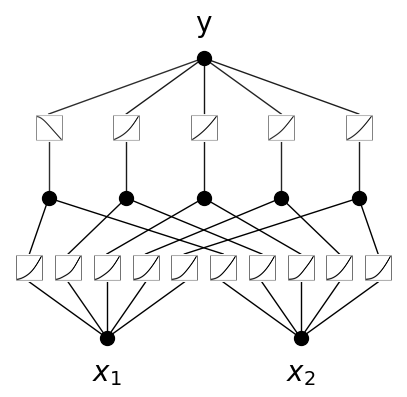
모델 학습은 다음과 같이 .train() 메소드로 가능합니다. 여기서는 L-BFGS optimizer를 사용하였고, sparsity 부여를 위해 $\lambda$를 지정해 주었습니다.

# Train KAN
res = model.train(dataset, opt="LBFGS", steps=20, lamb=0.01, lamb_entropy=10.)

res['train_loss'], res['test_loss'] 로 손실함수의 히스토리에 접근할 수 있습니다.

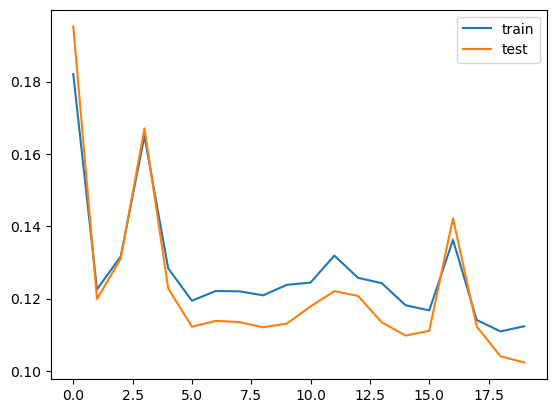
또한, 훈련 이후의 모델을 확인해보면 sparsity를 확인할 수 있습니다.

# After training
model.plot()

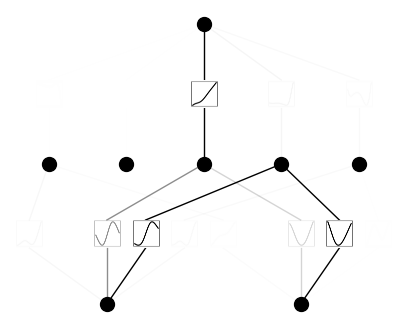
이를 바탕으로 가지치기(Prune) 작업을 진행하여, 불필요한 노드를 제거해줍시다.

# Prune
model2 = model.prune()
model2(dataset['train_input'])
model2.plot()

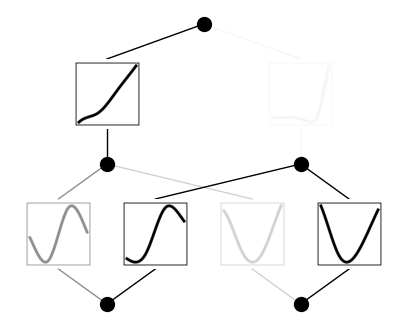
$[2,5,1]$-KAN이 $[2,1,1]$-KAN으로 줄어든 것을 확인할 수 있습니다. 또한, 아래 네 함수를 살펴보면 처음 두 개는 $\sin$ 함수를, 다음 두 개는 $x^{2}$ 함수를 따르는 것 처럼 보입니다. 실제로 적용가능한지 확인해보기 위해, 해당 함수를 symbolic function으로 바꾸었을 때 $R2$ 값이 어떻게 계산되는지 확인가능합니다. 제일 아랫줄의 제일 왼쪽 함수에 대해 확인하고자 한다면 model2.suggest_symbolic(0,0,0) 코드를 이용하면 됩니다. $(l,i,j)$은 각각 $l$번째 레이어, $i$번째 input, $j$번째 output을 연결하는 activation function을 지칭합니다.

function , r2
sin , 0.9967146515846252
gaussian , 0.9280341863632202
tanh , 0.8861169815063477
sigmoid , 0.8810763359069824
arctan , 0.8664839863777161

실제로 실행해보면 위와 같이 후보군들과 계산된 R2 값을 제공합니다. $\sin$ 함수가 높은 정확도를 갖는다는 것을 알 수 있고, model2.fix_symbolic(0,0,0, "sin") 코드로 해당 activation function을 $\sin$ 함수로 고정시킬 수 있습니다. 이 경우 plot을 그려보면 고정되었음을 나타내주기 위해 해당 함수 부분이 빨간색으로 나타납니다.

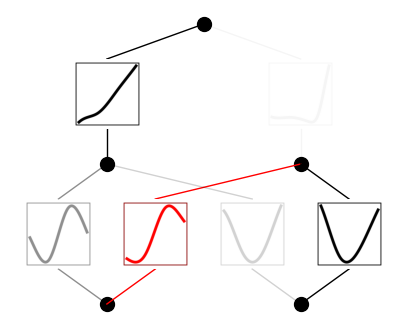
Classification

iris 데이터셋을 활용하여 분류 예시 문제를 살펴보겠습니다. 분류 문제의 경우, output vector를 $N \times c$차원 행렬로 지정해주어야 합니다 ($c$개의 클래스, $N$개의 데이터). 따라서 sklearn의 One-hot encoder를 이용해보도록 하겠습니다. 우선 데이터셋은 다음과 같이 구성해줍니다.

from sklearn.preprocessing import OneHotEncoder

enc = OneHotEncoder() 

# Iris dataset
iris = load_iris()
X = torch.tensor(iris.data, dtype=torch.float32)
y = enc.fit_transform(iris.target.reshape(-1, 1)).toarray()
y = torch.tensor(y, dtype=torch.float32)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

dataset = dict(train_input=X_train, train_label=y_train, test_input=X_test, test_label=y_test)

모델은 우선 $[4,9,3]$-KAN으로 설정하였습니다.

# Create KAN
model = KAN(width=[4,9,3], grid=3, k=3, seed=0)
model(X_train)
model.plot()

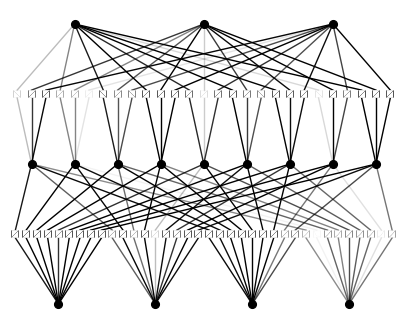
학습을 진행하기 위해, 손실함수를 설정해주어야 합니다. loss_fn 인자에 torch.nn.CrossEntropyLoss()를 설정해주고, 정확도를 별도의 metric으로 주어 히스토리가 남도록 설정해줍니다.

# Train KAN
from sklearn.metrics import accuracy_score

def train_acc():
    return torch.mean((torch.argmax(model(dataset['train_input']), dim=1) == torch.argmax(dataset['train_label'], dim=1)).float())

def test_acc():
    return torch.mean((torch.argmax(model(dataset['test_input']), dim=1) == torch.argmax(dataset['test_label'], dim=1)).float())

res = model.train(dataset, opt="LBFGS", metrics=[train_acc, test_acc], steps=20, lamb=0.01, lamb_entropy=10., loss_fn=torch.nn.CrossEntropyLoss())

# Accuracy plot
fig, ax = plt.subplots()
ax.plot(res["train_acc"], label="train")
ax.plot(res["test_acc"], label="test")
ax.legend()
plt.show()

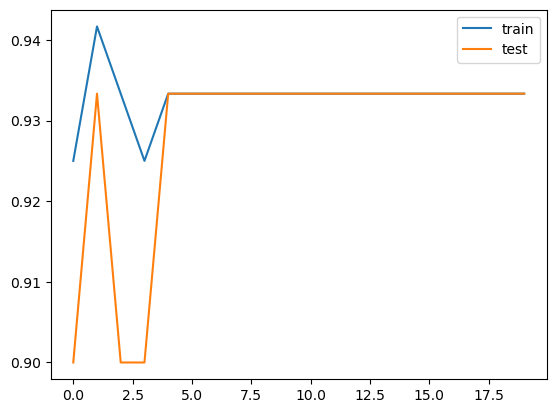Accuracy plot

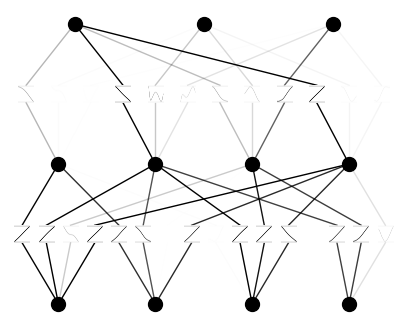
또한, 가지치기를 하면 다음과 같이 $[4,4,3]$-KAN으로 줄어든 것을 확인할 수 있습니다.

References

Leave a comment