Point Pattern on Linear Network

선형 네트워크Linear Network란 선분line segment들의 집합으로 구성되는 그래프 형태의 구조를 의미한다. 대표적으로 도시의 도로교통망이나 생태 분야에서 다루는 하천 네트워크 등이 이에 해당된다. 이번 글에서는 선형 네트워크 구조에서 주어지는 공간 점 과정에 대해 , intensity/density 추정이 어떻게 이루어지는지 설명하고자 한다. 주로 참고한 논문은 McSwiggan,G et al., Kernel Density Estimation on a Linear Network 이다.

Definition

Linear Network

선형 네트워크 $L\subset \mathbb{R}^{2}$은 2차원 유클리드공간에서 다음과 같이 주어지는 선분들의 집합이다.

\[\begin{align} l_{i}&=[\mathbf{u_{i}},\mathbf{v_{i}}] = \lbrace t\mathbf{u} + (1-t)\mathbf{v} : t\in[0,1]\rbrace \\ L &=\bigcup_{i=1}^{k}l_{i} \end{align}\]

선형 네트워크의 가장 큰 특징은, 각 선분들의 양 끝점 $\mathbf{u,v}$ 를 노드node로 하는 그래프 구조로 생각할 수 있다는 것이다. 즉 선분들의 집합으로부터 그래프를 생성할 수 있다. (Python에서는 momepy라는 패키지의 momepy.gdf_to_nx() 함수로 GeoDataFrame 객체를 networkx.Graph 객체로 변환할 수 있다. 아래 그림 참고.)

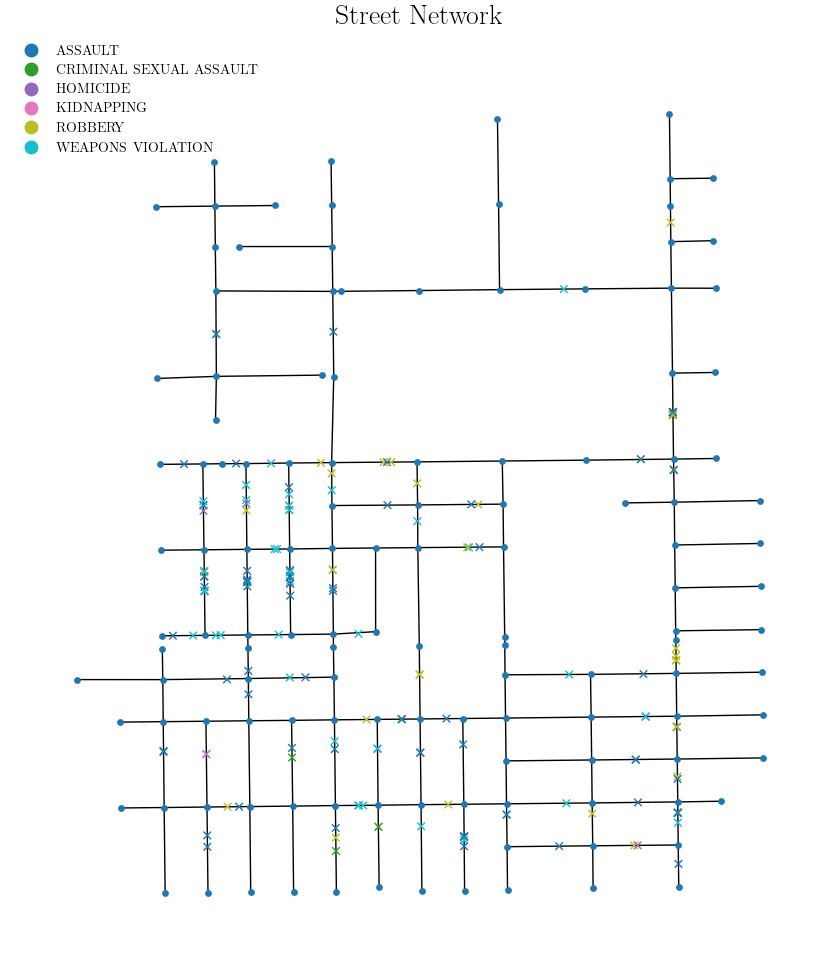
선형 네트워크 $L$에서 정의되는 point pattern $\mathbf{X}$를 Point pattern on Linear Network 라고 하며, 위 그림과 같이 각 evaluation이 그래프 위의 점으로 이루어진다는 것이 특징이다.

Geodesic

다만 일반적인 point pattern을 다룰 때와는 다른 접근 방식이 필요하다. 두 점 간의 거리를 측정할 때 기존의 유클리드 거리를 사용할 경우 그래프 구조를 반영하지 못하기 때문이다. 따라서, 그래프 구조 위에서 정의되는 거리를 사용해야 한다. 가장 널리 이용되는 것은 geodesic metric(혹은 shortest-path metric) 으로, 말 그대로 두 지점 간의 최단경로의 거리를 측정하는 metric이다.

\[d_{G}(u,v) = \inf\mathrm{len(\pi_{uv})}\]

으로 정의되며, 여기서 $\pi_{uv}$ 는 두 점 $u,v$을 잇는 경로를 나타낸다. 만일 두 점이 연결되지 않는다면 $d_{G}=\infty$ 로 정의된다. (아래는 nx.shortest_path() 함수를 이용해 구한 geodesic metric의 예시이다.)

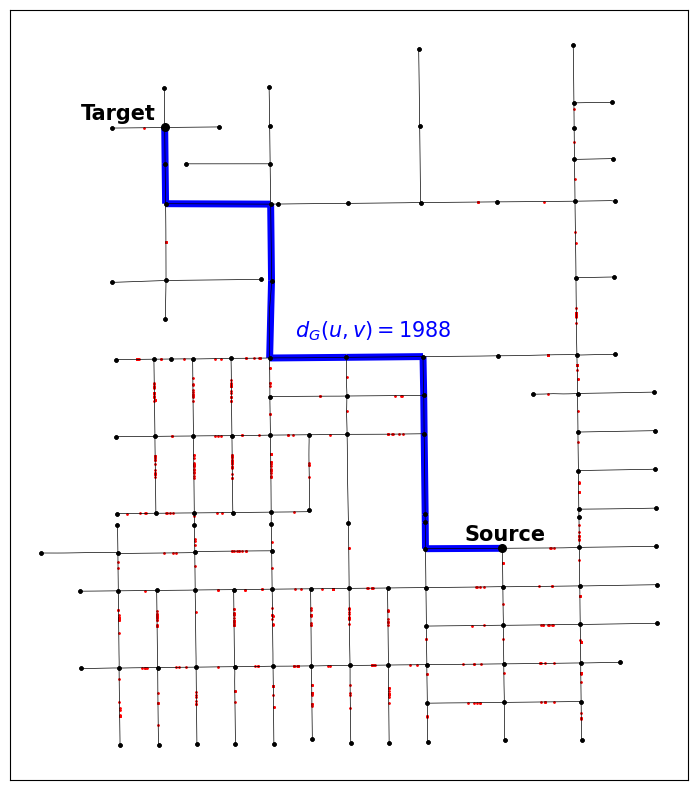Geodesic metric between source node(below) and target node(above)

선형 네트워크 상의 공간 점 과정에 대해서도 일반적인 공간 점 과정과 마찬가지로 intensity function $\lambda$를 다음과 같이 정의할 수 있다.

\[\mathrm{E}[N(B)] = \int _{B}\lambda (u) d_{1}u, B\subseteq L\]

여기서 $d_{1}u$는 각 선분에서 정의되는 1차원 적분을 의미한다.

Intensity estimator

일반적인 2차원 공간에서와 마찬가지로, 다음과 같은 밀도 추정량을 생각해보자.

\[\hat f(u) = \frac{1}{n}\sum_{i=1}^{n}K_{h}(d_{G}(u,x_{i})),\quad u\in L\tag{1}\]

이때 이러한 추정량은 mass-overflow 문제가 발생하게 된다. $u$와 패턴 $x_{i}$가 같은 선분 위에 존재하는 경우는 문제가 발생하지 않지만, 만일 다른 선분에 존재하는 경우 네트워크를 따라서 커널함수를 계산해야 한다 (아래 그림 참고). 그런데, 만일 커널 함수가 네트워크를 따라가다가 아래 그림처럼 나뉘어지는 형태가 되는 경우 $(1)$과 같이 정의를 하게 되면 동일한 커널을 각 엣지들에 부여하게 되며 커널의 총 적분값이 증가하게 된다. 즉, 커널의 전체 질량이 보존되지 않는 문제가 발생한다.

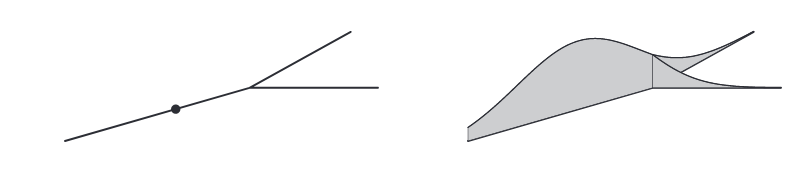Mass overflow problem. Source: Mcswiggan et al.

Equal-Split discontinuous Kernel

이러한 문제를 해결하기 위해 Okabe & Sugihara는 equal-split discontinuous kernel estimator를 제안했다. 이름에서 알 수 있듯이, 위 그림처럼 나뉘어지는 부분에 대해 커널 함수를 부여할 때 질량을 보존하기 위해 균등하게 나누어준다는 것이다. (아래 그림)

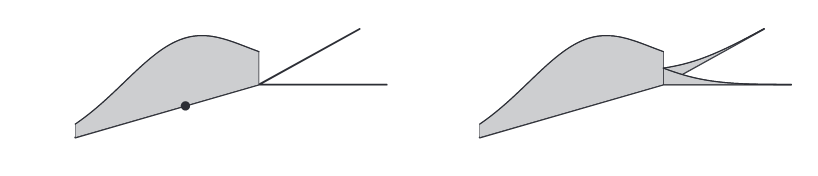Equal-split discontinuous kernel. Source: Mcswiggan et al.

다만 이러한 경우 커널 함수가 각 노드에서 불연속이 된다는 문제가 존재한다. 또한, 커널 함수가 전파되다가 그래프의 끝에 도달하게 될 경우(degree=1인 노드) truncation이 발생하게 되어 bias를 갖게 된다. 이를 edge-effect라고 한다. 이를 해결하기 위해 equal-split continuous kernel 역시 제안되었는데(Okabe, 2012), 이는 계산 비용이 훨씬 복잡하여 일반적으로는 discontinuous 버전을 사용한다.

Diffusion Kernel

2017년에 제안된 heat kernel(혹은 diffusion kernel) 기반의 방법은 네트워크 상에서 정의되는 heat equation의 solution으로 확률밀도를 정의한다.

Heat Equation

$\mathbb{R}$에서 정의되는 Brownian motion $\lbrace X(t):t\ge 0\rbrace $ 은 임의의 time points $0\le t_{1}< t_{2},<\cdots< t_k$ 에 대해

\[X(t_{2})-X(t_{1}),\cdots,X(t_{k})-X(t_{k-1}) \overset{iid}{\sim} N(\mathbf{0}, \mathrm{diag}(t_{2}-t_{1},\ldots,t_{k}-t_{k-1}))\]

인 random process를 의미한다. 평균이 0이고 분산이 $t$인 정규분포의 확률밀도함수를 $\phi_t(x)$ 라고 나타내면 $X(0)\sim p$ 일 때, $X(t)$의 확률밀도함수는 다음과 같이 주어진다.

\[f_{t}(x) = \int p(u)\phi_{t}(x-u)du\]

이때, 위 $f_{t}(x)$는 초기값이 $f_{0}=p$ 인 heat equation

\[\frac{\partial f}{\partial t}=\frac{1}{2}\cdot \frac{\partial^{2}f}{\partial x^{2}} \tag{2}\]

의 해가 된다.

On a Linear Network

앞서 살펴본 것과 같이 일반적으로 사용하는 가우시안 커널은 heat kernel로 사용될 수 있다. 다만, 네트워크 구조에서는 Brownian motion이 다르게 정의되는데, 만일 Brownian motion이 네트워크의 (차수가 $d$인) 노드에 도달하면, 이후에는 $1/d$ 의 균등한 확률로 $d$개의 연결된 엣지(기존의 엣지 포함) 중 하나로 이어진다.

선형 네트워크 위의 Brownian motion에 대한 $t$ 시점의 확률밀도를 $f_{t}(x),x\in L$ 라고 두면 이는 앞선 heat equation $(2)$를 만족한다. 추가적으로, 임의의 노드 $v\in V(L)$에서 $f_{t}$는 연속이고 ($V(L)$ 은 노드집합) 다음과 같은 heat flow conservation을 만족해야 한다.

\[\sum_{v'\sim v}\frac{\partial f}{\partial x_{[v,v']}}\bigg\vert_{v}= 0\]

여기서

\[\frac{\partial f}{\partial x_{[v,v']}}\bigg\vert_{v} =\lim_{h\to0}\frac{f(v+h(v'-v))}{h\Vert v-v'\Vert}\]

는 노드 $v$에서 인접엣지로 연결된 노드 $v’$ 방향으로의 변화율을 의미한다. 즉, 위 conservation의 의미는 노드에서 다음 단계의 Brownian motion이 나아가는 방향이 보존된다는 것으로 볼 수 있다.

또한 선형 네트워크 상에서 heat equation의 해는 다음과 같은 형태로 구해진다.

\[f_{t}(x) = \int_{L}p(u) K_{t}(x\mid u)d_{1}u\]

여기서 주어지는 $K_{t}$를 heat kernel 이라고 하며, 명시적인 형태는 아래 정리로 주어진다.

Kostrykin et al., 2007

선형 네트워크의 heat kernel은 다음과 같다.

\[K_{t}(u\mid x) = \sum_{\pi}a(\pi )\phi_{t}(\mathrm{len}(\pi ))\]

여기서 $\pi$는 $x\in L$에서 $u\in L$로 가는 경로를 의미하며, 모든 경로에 대해 위 합을 계산한다. 또한

\[a(\pi) = \prod_{v_{i}\in \pi}\left(\frac{2}{\mathrm{deg}(v_{i})}-\delta_{i}\right)\]

이고 $\delta_{i}=\mathbf{1}(e_{i}=e_{i-1})$ 을 나타낸다. 즉, $\delta_{i}=1$인 경우는 경로가 노드 $v_{i}$에서 반사직전 노드로 다시 진행되는 경우를 의미한다.

위 정리를 살펴보면, heat kernel은 모든 경로에 대해 합을 계산하기 때문에 계산이 매우 복잡할 것이라고 추측할 수 있다. 그러나 실제 계산은 iterative한 알고리즘을 이용하며, 수렴 속도가 충분히 빨라 기존의 equal-split estimator보다 훨씬 빠른 속도로 계산이 이루어진다고 한다.

이러한 heat kernel을 기반으로 다음과 같이 intensity에 대한 diffusion estimator를 정의할 수 있다.

\[\hat\lambda(u) = \sum_{i=1}^{n}K_{\sigma^{2}}(u\mid x_{i}),\quad u\in L\]

Diffusion estimator의 경우, 앞서 언급한 edge effect가 발생하지 않는다는 특징도 존재하는데, 이로 인해 edge-correction과 같은 작업을 해줄 필요가 없다는 것은 계산 속도의 측면에서 큰 장점이라고 볼 수 있다.

Python Implementation

networkx, shapely, geopandas 등의 패키지를 기반으로 diffusion estimator를 계산할 수 있는 패키지를 만들었으며(링크), Linnet() 클래스로 선형 네트워크 객체를 생성하고 다루도록 하였다. (R의 spatstat 패키지 차용)

필요한 패키지는 다음과 같다. 데이터 예시는 링크된 저장소에서 다운로드할 수 있다.

import geopandas as gpd
from linnet import Linnet, discretize_network, plot_network
from diffusion import diffusion
import matplotlib.pyplot as plt

crimes = gpd.read_file('data/crimes.shp')
streets = gpd.read_file('data/streets.shp')
crimes.crs == streets.crs

Linnet 객체는 다음과 같이 생성할 수 있다. 네트워크 정보로는 각 엣지의 geometry가 지정된 geopandas.GeoSeries 혹은 GeoDataFrame 객체를 주어야 한다.

linnet = Linnet(streets)

# Plot
fig, ax = plt.subplots(1, 1, figsize=(5, 5))
plot_network(linnet, ax=ax)
plt.show()

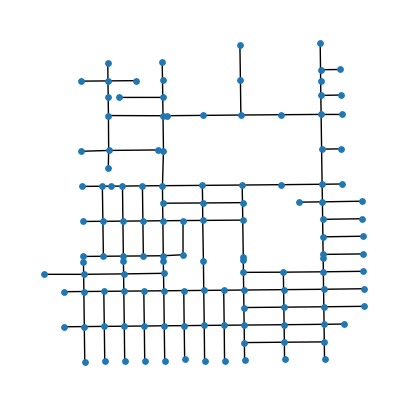
diffusion() 함수를 이용하여 diffusion estimator를 추정할 수 있다. bw는 커널의 대역폭을 의미하며, resolution은 추정 과정에서 네트워크를 균등하게 나눌 때 해상도를 의미한다. 해상도가 작을 경우 더 smooth한 추정 결과를 그릴 수 있지만 많은 계산 시간이 요구된다.

intensity = diffusion(linnet=linnet, points=crimes, bw=300, resolution=20)

# Plot
fig, ax = plt.subplots(1, 1, figsize=(7, 7))
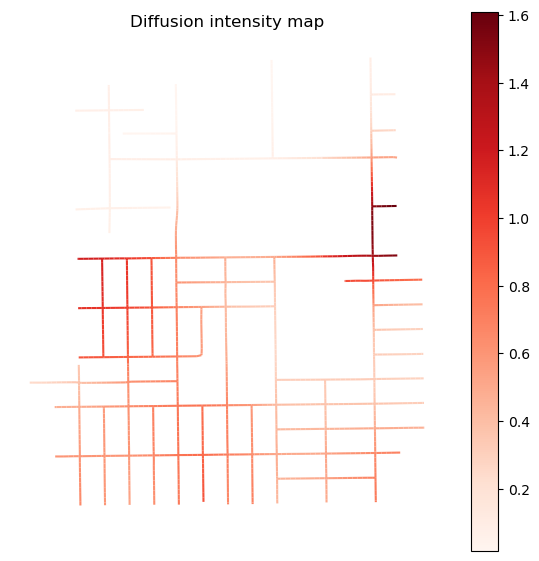
intensity.plot(column='intensity', cmap='Reds', legend=True, ax=ax)
ax.set_axis_off()
ax.set_title('Diffusion intensity map')
plt.show()

References

Leave a comment