Monte Carlo Sampling

Generating random samples

이번 글에서는 주어진 확률분포로부터 랜덤 샘플들을 생성하는 방법에 대해 살펴보도록 하자.

Simple method

만약 표본을 추출하고자 하는 대상 확률분포가 분포함수(cdf)로 주어지고, 그것의 역함수를 구할 수 있다면 다음 정리로부터 쉬운 표본추출이 가능하다.

Theorem

만약 확률변수 $U$가 균등분포 $\mathrm{Unif}[0,1]$ 을 따르면, 새로운 확률변수 $F^{-1}(U)$ 는 대상 분포 $F$를 따른다.

증명.

\[\begin{align} P(F^{-1}(U)\leq x) &= P(U\leq F(x))\\ &= F(x) \end{align}\]

즉, 위 정리로부터 우리는 균등분포로부터의 난수(0과 1 사이)만 추출할 수 있다면 그것의 역함수를 취해 대상 분포의 표본으로 삼을 수 있다.

Example. Standard Normal

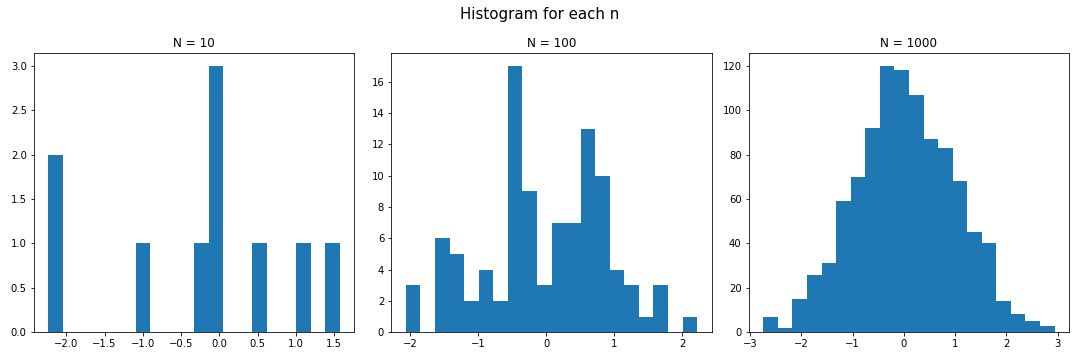
Python의 scipy.special.ndtri 는 표준정규분포 $N(0,1)$ 의 누적분포함수의 역함수를 제공한다. 이를 이용하여 다음과 같이 표준정규분포로부터의 random sampling을 수행할 수 있다.

# Monte Carlo sampling

from scipy.special import ndtri
import numpy as np 
import matplotlib.pyplot as plt

# Generate random samples from uniform[0,1]

ns = [10, 100, 1000]
np.random.seed(11)

# plot histogram of result for each n

fig, axes = plt.subplots(1,3, figsize=(15,5))
fig.suptitle("Histogram for each n", fontsize = 15)

# for n in ns:
for idx, n in enumerate(ns):
    ax = axes[idx]
    ax.hist(ndtri(np.random.rand(n)), bins=20)
    ax.set_title(f"N = {n}")

fig.tight_layout()
plt.show()

Importance sampling

랜덤표본추출을 사용하는 가장 큰 이유는 어떤 확률변수의 함수에 대한 적분값(기댓값)을 구하고자 할 때 몬테카를로 방법을 사용하기 위함이다. 즉, 확률변수 $x$ 에 대한 함수 $\phi(x)$ 의 기댓값을

\[\mathbb{E}\phi(x) = \int \phi(x)\pi(x)dx\]

로 구해야 하지만, 직접 적분하는 것이 어려운 상황이 많기 때문에, 우리는 몬테카를로(Monte Carlo) 방법을 이용하여 다음과 같이 적분의 근사값을 계산한다.

\[\mathbb{E}\phi(x)\approx \sum_{n=1}^{N}W_{n}\phi(x_{n})\]

여기서 $x_n$ 은 target distribution $\pi(x)$로부터 추출된 $N$개의 표본을 의미한다. 그런데, 앞서 살펴본 것처럼 추출 대상분포의 누적분포함수 및 그것의 역함수가 쉽게 구해지면 가능하지만, 대부분의 계산 상황에서 역함수를 구하는 것은 매우 어렵기 때문에 importance sampling(중요도 추출 혹은 중요도 샘플링) 기법을 이용한다.

Direct importance sampling

Direct importance sampling에서는 대상 분포 $\pi(x)$ 의 형태를 알고있지만, 이로부터 샘플링이 어려운 상황을 고려한다. $\pi(x)$로부터의 표본추출이 어렵기 때문에, 표본 추출이 보다 쉬운 표준정규분포 등을 proposal distribution(제안분포)로 삼고 그것으로부터 표본추출을 진행한다. 이를 Direct importance sampling(직접 중요도 추출)이라고 한다. 원리는 다음과 같이 매우 간단하다.

\[\int\phi(x)\pi(x)dx = \int\phi(x)\frac{\pi(x)}{q(x)}q(x)dx\]

즉, 기댓값을 대상 분포에 대해 취하는 것이 아닌, 제안분포에 대해 취함으로써 계산한다. 또한, 위 식으로부터 제안분포가 $0$이 되면 안된다는 것을 확인할 수 있고, 몬테카를로 근사는 다음과 같이 이루어진다.

\[\mathbb{E}\phi(x)\approx \frac{1}{N_{s}}\sum_{n=1}^{N_{s}} \frac{{\pi(x_{n})}}{q(x_{n})}\phi(x_{n})= \frac{1}{N_{s}}\sum_{n=1}^{N_{s}}\tilde w_{n}\phi(x_{n})\]

이로부터 얻은 결과는 실제 기댓값 $\mathbb{E}\phi(x)$ 에 대한 불편추정량(unbiased estimator)이 된다.

Self-normalized importance sampling

만일 대상분포 $\pi(x)$ 가 형태를 특정하기 어려우면 직접 중요도 추출을 진행하기 어렵다. 예를 들어, 대상분포가 조건부 확률분포 $p(x\vert y)$ 형태로 주어지는 경우, 분포를 특정하기 어려운 경우가 많다. 이러한 경우 다음과 같은 unnormalized target distribution

\[\begin{align} \tilde\gamma(x)&= Z\pi(x)\\ Z &= \int\tilde\gamma(x)dz \end{align}\]

의 특정이 더 쉽고, 이때 normalization constant $Z$ 를 중요도 추출을 이용해 근사하게 된다. 이러한 방법을 self-normalized importance sampling(SNIS)라고 하는데, 대상분포가 조건부 확률분포 $p(x\vert y)$ 인 경우 $\tilde\gamma(x)=p(x,y),Z=p(y)$ 가 된다.

구체적으로 살펴보면, SNIS의 근사 과정은 다음과 같다.

\[\begin{align} \mathbb{E}\phi(x) &= \int \phi(x)\pi(x)dx \\ &= \frac{{\int\phi(x)\tilde\gamma(x)dx}}{{\int\tilde\gamma(x)dx}}\\ &= \frac{{\int[\frac{{\tilde\gamma(x)}}{q(x)}\phi(x)]q(x)dx}}{{\int[\frac{{\tilde\gamma(x)}}{q(x)}]q(x)dx}}\\ &\approx \frac{\frac{1}{N_{s}}\sum_{n=1}^{N_{s}}\tilde w_{n}\phi(x_{n})}{\frac{1}{N_{s}}\sum_{n=1}^{N_{s}}\tilde w_{n}} \tag{*} \end{align}\]

여기서 unnormalized weights $\tilde w$ 는 다음과 같이 정의된 것이다.

\[\tilde w_{n} =\frac{\tilde \gamma(x_{n})}{q(x_{n})}\]

또한, 마지막 식 ($\star$)을 다음과 같이 간단하게 쓸 수도 있다.

\[\begin{align} \mathbb{E}\phi(x)&\approx \sum_{n=1}^{N_{s}}W_{n}\phi(x_{n})\\ W_{n} &= \frac{\tilde w_{n}}{\sum_{n^{\prime}=1}^{N_{s}}\tilde w_{n^{\prime}}} \end{align}\]

References

• Probabilistic Machine Learning - Advanced Topics