Neural ODE and FFJORD
Neural ODE
Neural ODENeural Ordinary Differential Equation를 다루기 전에 우선 깊이가 $L$인 (Hidden layer의 수가 $L$인) Residual NetworkResnet를 생각해보자 (아래 그림).
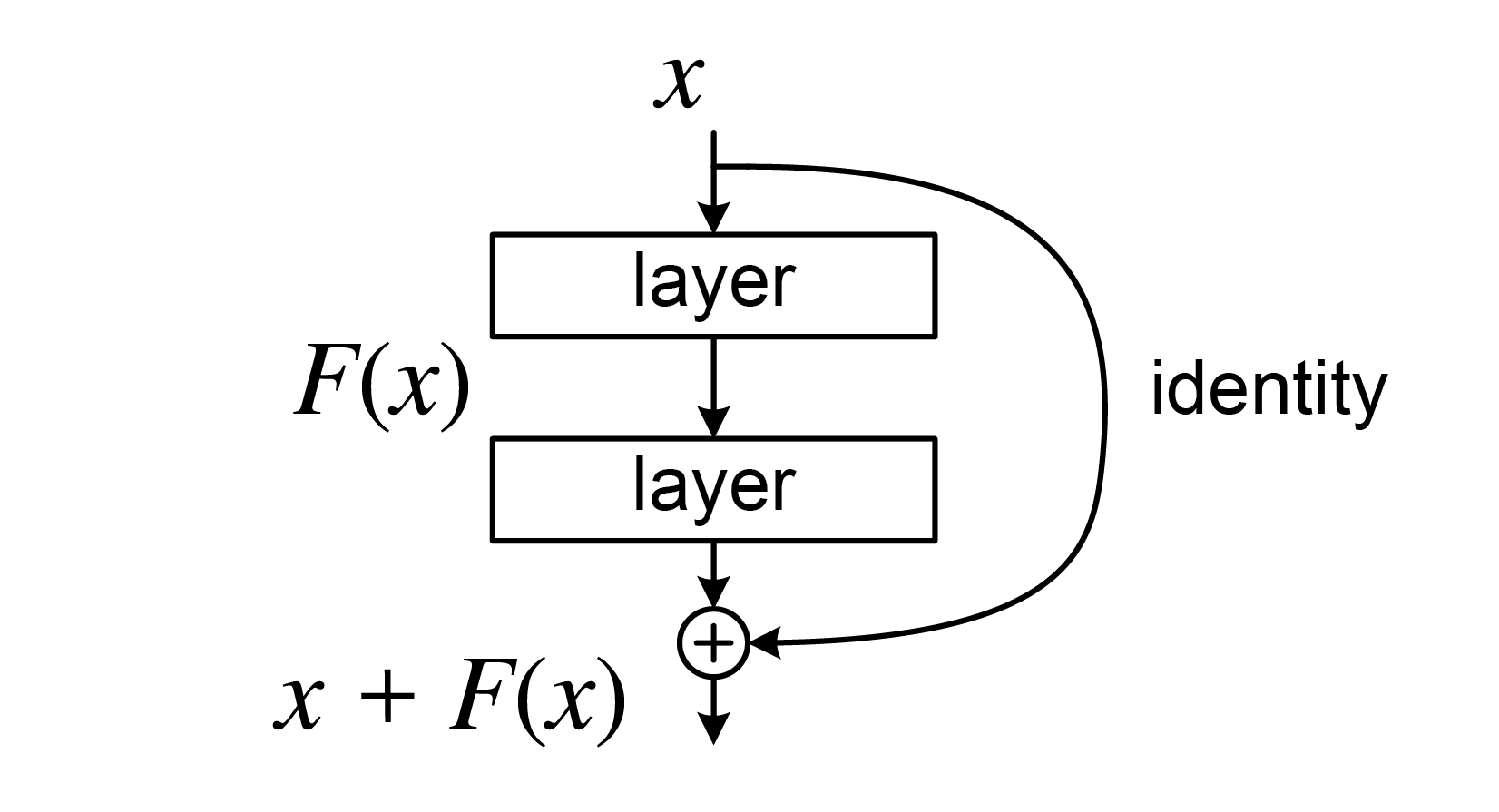 Residual network (He et al., 2015)
Residual network (He et al., 2015)
일반적으로 Resnet은 각 레이어에 대해 다른 파라미터를 적용하고 잔차항이 두 레이어에 걸쳐 더해지지만, 여기서는 각 레이어가 동일한 함수 $f_{\theta}$로 주어지고 각 레이어마다 잔차항이 추가된다고 가정하자. 그러면 위 네트워크의 구조는 다음과 같이 표현할 수 있다.
\[\begin{align} h_{\theta}(X) &= z_{L}\\ z_{L}&= z_{L-1} + f(z_{L-1},\theta, L-1)\\ \vdots\\ z_{1}&= z_{0} + f(z_{0}+\theta,0)\\ z_{0}&= X \end{align}\]여기서 $X$는 입력 데이터를 나타낸다.
Definition
Resnet에서는 각 레이어가 불연속적으로 주어진다. 즉, 각각의 레이어가 $1\sim L$ 번째 레이어에 대응되기 때문에, 위 식과 같이 $\lbrace z_{n}\rbrace $ 형태의 sequence로 나타낼 수 있다. Neural ODE는 미분 방정식을 통해 ResNet의 레이어를 연속적으로 확장한 것으로 볼 수 있다. 즉, 각 레이어에서의 상태 $z(t)$가 시간 $t$에 따라 변화하는 것으로 정의한다. 이때, $z(t)$는 다음과 같은 미분 방정식을 만족한다.
\[\begin{align} h_{\theta}(X) &= z(1) \\ \dot z(s) &= f(z(s),\theta, s)\quad s\in[0,1]\\ z(0) &= X \\ \end{align}\]여기서 $s$를 pseudo-time 이라고 하며, $z(s)$는 $s$에 따라 변화하는 상태를 나타낸다. 이때, $f(z(s),\theta, s)$는 $z(s)$에서의 gradient를 나타내며, $f$는 연속이고 미분가능한 함수이다. 일반적으로 $f$는 neural network 구조를 갖는다.
Solving ODE
위 상미분방정식의 초기값 문제를 풀면 $z(s)$를 구할 수 있다. 해는 다음과 같이 주어진다.
\[z(s) = X + \int_{0}^{s} f(z(t),\theta,t)dt\]Adjoint State Method
$\dot z(s) = f(z(s),\theta, s)$를 푸는 것과 동시에, $\theta$에 대한 그래디언트 $\frac{\partial L}{\partial \theta}$가 계산되어야 모델의 학습을 진행할 수 있다 (여기서 $L$은 손실함수를 나타낸다). 다만, $\frac{\partial L}{\partial \theta}$를 직접 계산하기는 어렵다. 이때, Adjoint State Method를 사용하면 $\frac{\partial L}{\partial \theta}$를 효율적으로 계산할 수 있다.
Adjoint State
Pseudo-time $s$에서의 Adjoint state $a(s)$는 다음과 같이 정의된다.
\[a(s) = \frac{\partial L}{\partial z(s)}\]이때, 이를 바탕으로 joint state
\[(a(s), b(s)) = (\frac{\partial L}{\partial z(s)}, \frac{\partial L}{\partial \theta(s)})\]를 정의하면, 다음과 같은 미분방정식을 얻을 수 있다.
\[\begin{align} \dot a(s) &= -a(s)^{T}\frac{\partial f(z(s),\theta,s)}{\partial z}\\ \dot b(s) &= -a(s)^{T}\frac{\partial f(z(s),\theta,s)}{\partial \theta}\\ a(1) &= \frac{\partial L}{\partial z(1)}\\ b(1) &= 0 \end{align}\]위 ODE를 풀면 $b(0) = \frac{\partial L}{\partial \theta}$를 얻을 수 있다.
FFJORD
Neural ODE를 이용하여 생성모델을 학습하는 대표적인 방법으로 FFJORDFFJORD: Free-form Jacobian of Reversible Dynamics 모델이 있다. 이는 Normalizing Flow의 변형으로 볼 수 있다. Noramlizing flow가 상태 $t=1,\ldots,T$에서 변수 변환(Change of variable)을 통해 확률밀도함수를 학습하는 것처럼, FFJORD는 연속적인 상태 $t\in[0,1]$에서 변수 변환을 통해 확률밀도함수를 학습한다.
일반적인 생성모델에서와 같이, 잠재변수 $Z$와 샘플 $X$를 고려하자. FFJORD는 다음과 같은 미분방정식을 풀어 확률밀도함수를 학습한다.
\[\begin{align} X &= z(1)\\ \dot z(s) &= f(z(s),\theta,s)\\ z(0) &= Z \sim p_Z \end{align}\]이때, Neural ODE에서처럼 $f(z(s),\theta,s)$는 neural network 구조를 갖는다. 위 미분방정식을 이용해 모델을 학습하기 위한 손실함수 $L$로 다음과 같은 Negative Log-Likelihood를 사용한다.
\[\min_{\theta} L(\theta) = -\mathbb{E}_{Z\sim p_Z}\left[\log p_{\theta}(X)\right]\]Theorems
FFJORD의 학습 과정에 다음과 같은 정리가 이용된다.
Theorem
\[\begin{align} \frac{d}{ds} \log p_{\theta}(z(s)) &= -\text{Tr}\left(\frac{\partial f(z(s),\theta,s)}{\partial z}\right)\\ &= -\nabla_{z} f(z(s),\theta,s) \end{align}\]여기서 $\nabla_z$는 divergence operator를 나타내며, 이는 Jacobi’s formula를 이용하여 증명할 수 있다.
Log likelihood
위 정리를 이용하면, 로그가능도 $\log p_{\theta}(X)$를 다음과 같이 ODE로 표현할 수 있다.
\[\begin{align} \log p_{\theta}(X) &= l(1) \\ \dot l(s) &= -\nabla_{z} f(z(s),\theta,s)\\ l(0) &= \log p_Z(z(0)) \end{align}\]혹은 다음과 같은 역방향 ODE를 이용하여 표현할 수도 있다.
\[\begin{align} \log p_{\theta}(X) &= \log p_Z(z(0)) + l(0) \\ \dot l(s) &= -\nabla_{z} f(z(s),\theta,s)\\ l(1) &= 0 \end{align}\]따라서, 로그가능도는 위 두 방향 중 하나의 ODE를 풀어 얻을 수 있다. 다만, 이 경우 $z(s)$를 모든 $s$에 대해 저장해야 하므로, 메모리 사용량이 늘어날 수 있다는 문제가 존재한다. 이를 해결하기 위해, 다음과 같이 $z(s), l(s)$에 대해 동시적으로 역방향 ODE를 풀어나가는 방법을 사용할 수 있다.
\[\begin{align} \log p_{\theta}(X) &= p_Z(z(0)) + l(0)\\ \frac{d}{ds}\begin{bmatrix}z(s)\\l(s)\end{bmatrix} &= \begin{bmatrix}f(z(s),\theta,s)\\-\nabla_{z} f(z(s),\theta,s)\end{bmatrix}\\ \begin{bmatrix}z(1)\\l(1)\end{bmatrix} &= \begin{bmatrix}X\\0\end{bmatrix} \end{align}\]위 ODE를 풀기 위해서는 역전파 과정에서 $\nabla_z f=\text{Tr}\left(\frac{\partial f(z(s),\theta,s)}{\partial z}\right)$ 에 대한 역전파를 진행해야 한다. 그러나 이를 계산하는 것은 $O(d)$만큼의 계산량이 필요하다(여기서 $d$는 $z$의 차원). 이를 해결하기 위해 FFJORD에서는 다음과 같은 트릭을 사용한다.
Hutchinson’s Trace Estimation
임의의 행렬 $A\in \mathbb{R}^{d\times d}$에 대해, $A$의 trace는 다음과 같이 추정할 수 있다.
\[\text{Tr}(A) = \mathbb{E}_{\epsilon}\left[\epsilon^{T}A\epsilon\right]\]여기서 $\epsilon$은 $d$차원의 표준정규분포를 따르는 랜덤벡터이다. 이를 이용하면, $\nabla_z f$를 다음과 같이 추정할 수 있다.
\[\begin{align} \log p_\theta(X) &= \log p_Z(z(0)) - \int_0^1 \text{Tr}\left(\frac{\partial f(z(s),\theta,s)}{\partial z}\right)ds\\ &= \log p_Z(z(0)) - \int_0^1 \mathbb{E}_{\epsilon}\left[\epsilon^{T}\frac{\partial f(z(s),\theta,s)}{\partial z}\epsilon\right]ds\\ &\approx \log p_Z(z(0)) - \int_0^1 \epsilon^{T}\frac{\partial f}{\partial z}\epsilon ds \end{align}\]결론적으로 divergence 대신 $\epsilon^{T}\frac{\partial f}{\partial z}\epsilon$를 사용하여 역전파를 진행한다는 것인데, 이러한 방법의 장점은 계산량이 $O(1)$로 줄어든다는 것이다. 이를 바탕으로 다음과 같이 ODE를 다시 구성할 수 있다.
\[\begin{align} \log p_{\theta}(X) &= p_Z(z(0)) + l(0)\\ \frac{d}{ds}\begin{bmatrix}z(s)\\l(s)\end{bmatrix} &= \begin{bmatrix}f(z(s),\theta,s)\\-\epsilon^{T}\frac{\partial f(z(s),\theta,s)}{\partial z}\epsilon\end{bmatrix}\\ \begin{bmatrix}z(1)\\l(1)\end{bmatrix} &= \begin{bmatrix}X\\0\end{bmatrix} \end{align}\]그래디언트의 계산은 Neural ODE와 동일하게 Adjoint State Method를 사용하여 진행하면, FFJORD 모델을 학습할 수 있다.
References
- He, K., Zhang, X., Ren, S., & Sun, J. (2015). Deep Residual Learning for Image Recognition (arXiv:1512.03385). arXiv. https://doi.org/10.48550/arXiv.1512.03385
- Chen, R. T. Q., Rubanova, Y., Bettencourt, J., & Duvenaud, D. (2019). Neural Ordinary Differential Equations (arXiv:1806.07366). arXiv. https://doi.org/10.48550/arXiv.1806.07366
- Grathwohl, W., Chen, R. T. Q., Bettencourt, J., Sutskever, I., & Duvenaud, D. (2018). FFJORD: Free-form Continuous Dynamics for Scalable Reversible Generative Models (arXiv:1810.01367). arXiv. https://doi.org/10.48550/arXiv.1810.01367
Leave a comment