Optimal Transport

Optimal Transport는 하나의 확률분포를 다른 확률분포로 옮기는데 필요한 비용을 계산하는 문제라고 생각하면 된다. 즉, 두 확률분포 간의 거리를 측정하는 것이 주요 목적이다. 이러한 문제는 다양한 분야에서 활용되는데, 예를 들어 이미지 처리에서는 두 이미지 간의 색상 분포를 매핑하는데 사용할 수 있다. 이번 포스트에서는 Optimal Transport의 개념과 이를 구현하는 방법에 대해 알아보도록 하자.

Distance of densities

확률변수 $X,Y$가 분포 $P,Q$를 갖고, 확률밀도함수를 각각 $p,q$라고 하자. 확률밀도함수 간의 거리를 측정하는 방법에는 여러 종류가 있다. 대표적으로, 다음과 같은 것들이 있다. (각각 Total Variation, Hellinger distance, L2 distance 이고 $\mu$는 Lebesgue measure를 의미한다.)

\[\begin{align} TV(P,Q) &:= \frac{1}{2}\int\vert p-q\vert d\mu\\ H(P,Q) &:= \sqrt{\int(\sqrt{p}-\sqrt{q})^{2}} d\mu\\ L_{2}(p,q) &:= \int (p-q)^{2}d\mu \end{align}\]

그러나, 이러한 거리 개념들은 분포 간의 거리를 측정할 때 위치 정보를 반영하지 못한다는 문제가 있다. 아래 그림을 살펴보면 이해가 가능하다.

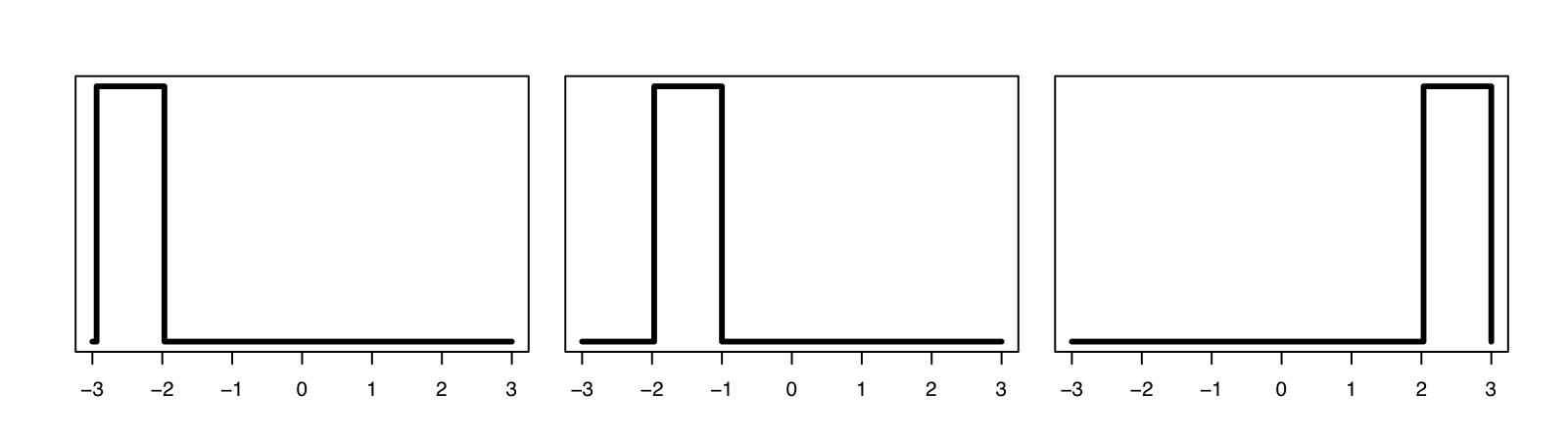
위 세 개의 밀도함수는 TV, Hellinger distance, L2 distance 등의 관점에선 서로 동일한 거리를 갖는다. 그러나, 1번과 2번의 밀도함수가 더 가깝다는 정보를 반영하고 싶다면 해당 거리함수는 사용할 수 없게 된다. 이러한 관점을 반영한 것이 optimal transport이다.

Optimal Matching

우선, optimal transport를 살펴보기 이전에 간단한 warm-up example을 살펴보도록 하자.

각각 $n$개의 점으로 구성된 두 개의 집합 $(\mathbf{x}_{1},\ldots,\mathbf{x}_{n})$, $(\mathbf{y}_{1},\ldots,\mathbf{y}_{n})$을 생각하자. 이때, 각 집합의 원소는 $\mathcal{X}$의 원소이다. 매칭^matching이란, 두 집합 사이의 전단사함수^bijective를 의미한다. 이는 각 원소끼리의 대응인 $(i,j)\in \lbrace 1,\ldots,n\rbrace ^{2}$ 들로 표현할 수 있으며, 이를 permutation $\sigma$로 나타내기로 하자. 즉,

\[\mathbf{x}_{i}\mapsto \mathbf{y}_{\sigma_{i}}\]

와 같이 대응이 이루어진다 ($j=\sigma_{i}$ 로 대응). 그런데, 이러한 매칭은 $n!$ 개가 존재한다. 따라서, 최적의 매칭^{optimal matching}을 생각할 수가 있으며, 이를 위해서는 매칭의 비용을 측정하는 함수가 필요하다. 이를 cost function $C_{ij}=c(\mathbf{x}_{i},\mathbf{y}_{j})$로 나타내어 $\mathbf{x}_{i},\mathbf{y}_{j}$를 연결하는 것의 비용으로 정의하자.

그렇다면, 최적의 매칭을 찾는 것은 다음과 같은 최적화 문제로 나타낼 수 있다.

\[\min_{\sigma}E(\sigma ) = \sum_{i=1}^{n}c(\mathbf{x}_{i},\mathbf{y}_{\sigma_{i}}) \tag{OM}\]

이는 $n!$개의 $\sigma$를 탐색하여 풀 수 있지만, Hungarian algorithm을 이용하면 $O(n^{3})$ 시간에 풀 수 있는 문제가 된다는 것이 알려져 있다.

Optimal Transport

앞서 살펴본 optimal matching problem (식 $(\mathrm{OM})$)을 일반적인 상황으로 확장한 것이 optimal transport 문제라고 생각하면 된다. Optimal matching은 다음과 같은 상황에서 최적화 문제가 잘 정의되지 않기 때문이다.

두 집합의 원소의 개수가 동일하지 않을 때
연속형 측도를 다룰 때 : 두 확률밀도함수 간의 optimal matching을 어떻게 정의할 것인가?

Mass Splitting

Optimal transport를 쉽게 이해하기 위해 다음과 같은 예시 상황을 생각해보자. 우선, $n$명의 사람(worker)과 $n$개의 작업(task)이 존재하여, 각 작업을 효율적으로 처리하고자 한다. 이때, 다음과 같이 각 사람과 작업에 대한 능력을 정의할 수 있다.

$\mathbf{x}_{i}$ : $i$번째 사람의 작업 수행 능력
$\mathbf{y}_{j}$ : $j$번째 작업이 요구하는 능력
여기서 능력이란, 단위 시간 내 일을 처리하는 능력이라기보다는, 종류를 의미한다고 보면 적절하다 (ex. 청소, 분해, 조립 등 : 아래 그림과 같이 좌표상의 위치로 표현가능함)

그러면, 앞서 살펴본 것 처럼 $(\mathbf{x}_{1},\ldots,\mathbf{x}_{n})$과 $(\mathbf{y}_{1},\ldots,\mathbf{y}_{n})$에 대한 optimal matching을 구할 수 있을 것이다. $n=5$일 때 다음 그림과 같이 optimal matching $\sigma^{\ast}$를 구할 수 있다.

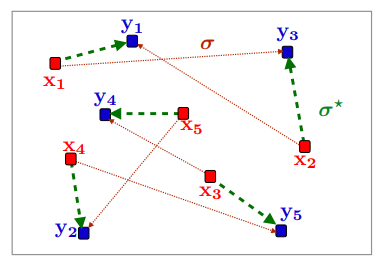Optimal matching when $n=5$ (Source : Murphy, 2023)

그런데, 실제 상황에서는 반드시 한 사람이 한 작업에 대응되어야 할 필요는 없다. 따라서, 사람의 능력을 나누어 여러 작업을 처리하도록 하거나, 한 작업을 나누어 여러 사람이 처리하도록 할 수 있다. 이러한 mass-splitting 세팅에서의 optimal matching을 다룬 것이 아래 Kantorovich의 설정이다.

Kantorovich formulation

Kantorovich의 설정에서는 더 일반적인 상황을 다룬다. 우선, 앞선 예시를 확장해보자.

$n$명의 작업자는 $(\mathbf{a}_{i},\mathbf{x}_{i})$로 나타난다. (for $i=1,\ldots,n$)
$\mathbf{a}_{i}$는 $i$번째 작업자가 제공가능한 시간을 의미한다.
$m$개의 작업은 $(\mathbf{b}_{j},\mathbf{y}_{j})$로 나타난다. ($n\neq m$일 수 있음)
$\mathbf{b}_{j}$는 $j$번째 작업에 필요한 소요 시간을 의미한다.

이 경우, 전체 작업자에 대한 능력의 합은

\[\sum_{i}\mathbf{a}_{i},\delta_{\mathbf{x}_{i}}\]

로 나타낼 수 있을 것이다. ($\delta$는 dirac delta measure를 의미함 : 한 점에서만 확률이 1로 정의되는 확률측도) 마찬가지로, 전체 작업에 대한 요구 능력의 합은 $\sum_{i}\mathbf{b}_{i},\delta_{\mathbf{y}_{i}}$ 로 나타낼 수 있다. 여기서 $\sum_{i}\mathbf{a}_{i}=\sum_{i}\mathbf{b}_{i}$ 라는 가정을 추가한다면, Kantorovich의 optimal transport는 다음과 같이 정의된다.

\[\mathrm{OT}(\mathbf{a,b}) \triangleq \min_{P\in \mathbb{R}^{n\times m}_{+},P\mathbf{1}_{n}=\mathbf{a},P^{\top}\mathbf{1}_{m}=\mathbf{b}} \langle P,C\rangle \triangleq \sum_{i,j}P_{ij}C_{ij}\]

정의가 어려워 보이지만, 행렬 $P$ 관점에서는 매우 간단하다. 우선 $n\times m$ 행렬 $P$의 $(i,j)$ 번째 원소는 각각 $i$번째 작업자가 $j$번째 작업에 사용하는 시간을 나타낸다. 따라서 $P\mathbf{1}_{n}=\mathbf{a}$와 $P^{\top}\mathbf{1}_{m}=\mathbf{b}$ 제약 조건이 필요하다. 즉, 위 최적화 문제는 이러한 행렬 $P$를 최적화하는 문제로 생각하면 되며, 이는 다음 그림과 같이 나타낼 수 있다.

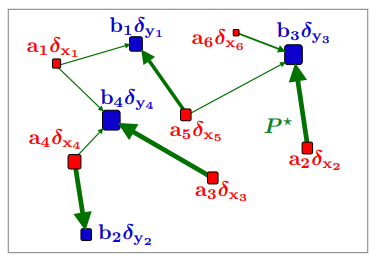Kantorovich Optimal matching when $n=5$ (Source : Murphy, 2023)

Monge Formulation

앞서 살펴본 Kantorovich 정의는 일반적인 discrete distribution간의 매칭으로 확장이 가능했다. 그런데, 이는 두 분포를 잇는 mapping의 관점에서는 적절한 정의가 아닐 수 있다. 하나의 확률분포를 다른 분포로 변환한다는 것은, 각 점 $\mathbf{x}_{i}$를 $\mathbf{y}_{j}$로 유일하게 연결해야 적절한데 Kantorovich의 정의는 하나의 점이 여러 개의 점에 대응될 수 있기 때문이다.

이를 해결하는 방법이 Monge의 정의이다. 이는 확률측도 $\mu$가 density function을 갖게끔만 가정하면, 간단하게 정의하여 해결된다. 이를 위해 우선 push-forward라는, 두 측도 간의 mapping을 정의하자.

함수 $T:\mathbb{R}^{d}\to \mathbb{R}^{d}$ 에 대해 분포 $P$의 push-forward를 다음과 같이 정의한다.

\[T_{\#}P(A) = P(\lbrace x:T(x)\in A\rbrace ) = P(T^{-1}(A)).\]

그러면 Monge optimal transport를 다음과 같이 정의할 수 있다.

\[\inf_{T} \int \Vert x-T(x)\Vert^{p}dP(x) \tag{1}\]

직관적으로는 분포 $P$를 $Q$로 옮기는데 필요한 비용을 측정하는 것이다. 만일 이를 최소로 하는 $T^{\star}$ 가 존재한다면 이를 optimal transport map이라고 하며, 다음 그림과 같다.

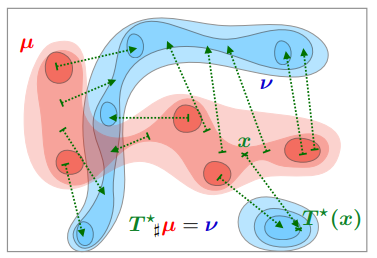Optimal Transport map (Source : Murphy, 2023)

다만 optimal transport map이 존재하지 않을 수 있다.

\[P=\delta_{0}\quad Q=\frac{1}{2}\delta_{-1}+ \frac{1}{2}\delta_{1}\]

여기서 $\delta_{x}$는 $x$에서의 Dirac delta function을 의미한다. 즉, $P$는 $x=0$에서 확률이 1이고, $Q$는 $x=-1,1$에서 확률이 1/2인 분포이다. 이러한 예시의 경우, 두 분포의 support가 다르기 때문에 $P$에서 $Q$를 매핑하는 사상이 존재하지 않게 된다. Monge optimal transport는 $P$의 support에 속하는 $x$를 $T(x)$로 옮기는 $T$를 찾는 것이기 때문에, 이러한 경우에는 optimal transport map이 존재하지 않는다.

또한, 실제로 optimal transport를 구하기 위해 push-forward $T$에 대한 최적화를 진행하려고 해도, 위 최적화 문제 $(1)$은 non-convex이라는 문제가 있다.

이를 해결하기 위해, 앞서 살펴본 Kantorovich formulation을 다시금 가져와서 이를 연속형 확률에 정의하고자 한다.

Kantorovich formulation - Revisited

이산형 확률분포에 대한 Kantorovich formulation은 행렬 $P$를 최적화하는 것이었다. 대신에, 결합확률분포들의 모임에서 결합확률분포를 최적화하는 것으로 문제를 변환하자.

\[\min_{P\in \mathbb{R}^{n\times m}_{+},P\mathbf{1}_{n}=\mathbf{a},P^{\top}\mathbf{1}_{m}=\mathbf{b}} \Rightarrow \min_{\pi\in \Pi(\mu,\nu)}\]

여기서 $\Pi$는 주변확률분포가 두 측도 (변환 대상)인 결합확률분포들의 모임을 의미한다. 구체적으로는 다음과 같이 정의된다.

\[\Pi(\mu,\nu) \triangleq \lbrace \pi \in \mathcal{P}(\mathcal{X}^{2}) : \forall A\subset \mathcal{X}, \pi(A\times \mathcal{X})=\mu(A),\pi(\mathcal{X}\times A)=\nu(A)\rbrace\]

이 경우 Optimal transport는 다음과 같이 정의할 수 있다.

\[\mathrm{OT}_{c}(\mu,\nu) \triangleq \inf_{\pi\in \Pi(\mu,\nu)}\int_{\mathcal{X}^{2}}cd\pi\]

이때, 목적함수 $c$가 metric(ex. L2 distance)으로 주어지는 경우, 위 최적화 문제의 해는 다음 Wasserstein distance로 변환된다.

Wasserstein Distance

Wasserstein distance에 대한 wikipedia의 직관적인 설명은 다음과 같다.

Intuitively, if each distribution is viewed as a unit amount of earth (soil) piled on $M$, the metric is the minimum “cost” of turning one pile into the other, which is assumed to be the amount of earth that needs to be moved times the mean distance it has to be moved.

직관적으로, 각 분포가 $M$에 쌓인 흙더미로 본다면, 이 거리(Wasserstein distance)는 한 더미를 다른 더미로 바꾸는 최소 “비용”이다. 이 비용은 이동해야 하는 토양의 양에 이동해야 하는 평균 거리를 곱한 것이라고 가정한다.

이러한 설명에서 Wasserstein distance를 ‘earth mover distance’라고도 부르기도 한다. Wasserstein distance는 다음과 같이 정의된다.

\[W_{p}(P,Q) = \bigg(\inf_{J\in \mathcal{J}(P,Q)}\int\Vert x-y\Vert^{p}dJ(x,y)\bigg)^{\frac{1}{p}}\]

여기서 $\mathcal{J}(P,Q)$는 $(P,Q)$를 각각 marginal distribution으로 하는 모든 결합확률분포의 모임이다. 즉, $T_{X\#}J=P, T_{Y\#}J=Q$를 의미한다. Monge 정의와의 차이점은, Wasserstein distance로부터는 optimal transport가 항상 존재한다는 점이다.

$p=1$인 경우, 다음과 같이 간단한 형태를 얻을 수 있다.

\[W_{1}(P,Q) = \sup\bigg\lbrace \int f(x)dP(x)-\int f(x)dQ(x) : f\in\mathcal{F}\bigg\rbrace\]

여기서 $\mathcal{F}$는 $\vert f(y)-f(x)\vert\leq \Vert x-y\Vert$ 를 만족하는 함수집합을 의미한다.

$d=1$인 경우, Wasserstein distance는 다음과 같은 형태로 나타낼 수 있다.

\[W_{p}(P,Q)=\bigg(\int_{0}^{1}\vert F^{-1}(z)-G^{-1}(z)\vert^{p}dz\bigg)^{\frac{1}{p}}\]

여기서 $F,G$는 $P,Q$의 누적분포함수를 의미한다.

Geodesics

두 확률분포 $P_{0},P_{1}$이 있을 때, $c(0)=P_{0},c(1)=P_{1}$을 만족하도록 사상 $c:[0,1]\to\mathcal{P}$를 정의할 수 있다. 또한, 이렇게 만들어진 사상에 대해 길이 $L(c)$를 정의할 수 있는데, 이 경우 $L(c)=W_{p}(P_{0},P_{1})$을 만족하는 사상 $c$가 존재한다. 즉, $(P_{t}:0\leq t\leq 1)$ 은 $P_{0},P_{1}$을 연결하는 geodesic이 된다.

Barycenter

확률분포 $P_{1},\cdots, P_{N}$이 존재할 때, 확률분포들을 요약하여 하나의 분포로 나타내는 과정을 생각해보자. 일반적으로 확률분포들의 평균함수를(유클리드 평균) 사용하게 될 경우, 확률분포의 특성을 제대로 반영할 수 없다. 이를 해결하기 위해 중앙값과 유사하게 서로 간의 Wassestein distance를 계산하여, 중앙 분포를 대표 분포로 사용한다. 이를 barycenter라고 한다.

Optimization

Optimal transport를 구하는 최적화 풀이 방법에 대한 자세한 내용은 여기서는 생략하기로 한다.

(K. Murphy (2023)의 chapter 6에 잘 정리되어 있음)

Python Implementation

POT (Python Optimal Transport) 패키지를 이용하면 파이썬에서 optimal transport를 간단하게 구현할 수 있다.

Optimal Transport between 1D Gaussian

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import ot
import ot.plot
import scipy

n = 100
x = np.arange(n, dtype=np.float64)

# Gaussian distributions
a = scipy.stats.norm.pdf(x, loc=20, scale=5)
b = scipy.stats.norm.pdf(x, loc=60, scale=10)

# Loss matrix
M = ot.dist(a.reshape((n, 1)), b.reshape((n, 1)))
M /= M.max()

plt.subplots(1,1,figsize=(6,6))
plt.plot(x, a, label='Source distribution')
plt.plot(x, b, label='Target distribution')
plt.legend()
plt.show()

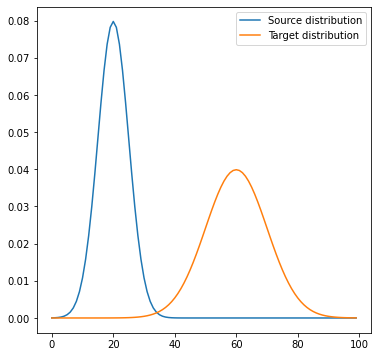
scipy로 위와 같은 두 가우시안 분포를 생성하여, 두 분포 간 Optimal Transport를 계산해보자.

plt.figure(2, figsize=(6, 6))
ot.plot.plot1D_mat(a, b, M, 'Cost matrix M')

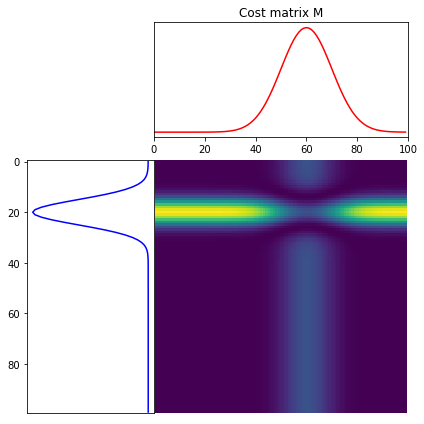
Cost matrix는 위와 같고, Sinkhorn 알고리즘을 사용하여 아래와 같이 최소 cost matrix를 구할 수 있다.

# Optimal transport
Gs = ot.sinkhorn(a, b, M, 1e-3, verbose=True)

plt.figure(3, figsize=(6, 6))
ot.plot.plot1D_mat(a, b, Gs, 'OT matrix Sinkhorn')

plt.show()

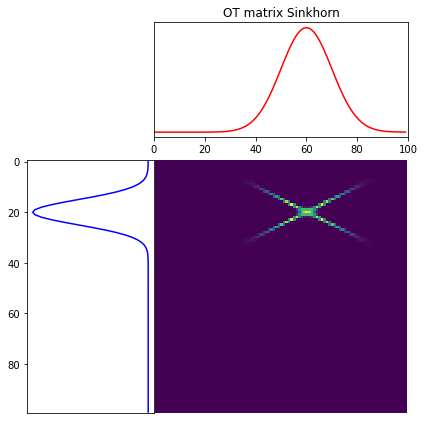
Image adaptation

Optimal transport는 이미지 데이터에 사용하기 좋은데, 한 이미지의 RGB 분포를 다른 이미지의 RGB 분포로 Transport하는 OT를 찾게 되면, 이미지의 colormap을 다른 이미지로 옮길 수 있게 된다. 이러한 과정을 image adaptation이라고 한다. 아래와 같은 두 이미지를 고려해보자.

위 두 이미지의 colormap을 산점도로 나타내면 다음과 같다.

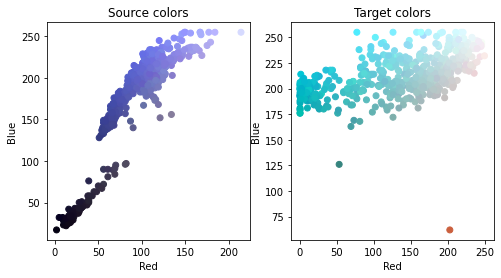
우리가 찾고자 하는 OT는 두 색상 분포간의 mapping이며, 이를 적용한 결과는 다음과 같다.

확인해보면, Target 이미지의 색상 분포가 기존 source 이미지에 학습된 것을 확인할 수 있다.

References

https://pythonot.github.io/
Murphy, K. P. (2023). Probabilistic machine learning: Advanced topics. The MIT Press.
서울대학교 M2480.001200 인공지능을 위한 이론과 모델링 강의노트

Optimal Transport

Distance of densities

Optimal Matching

Optimal Transport

Mass Splitting

Kantorovich formulation

Monge Formulation

Kantorovich formulation - Revisited

Wasserstein Distance

Geodesics

Barycenter

Optimization

Python Implementation

Optimal Transport between 1D Gaussian

Image adaptation

References

Leave a comment