Rényi Differential Privacy

Rényi Differential Privacy

Differential privacy는 초기 Dwork의 논문에서 $\epsilon$-DP, $(\epsilon,\delta)$-DP 형태로 제안되었습니다. 이후 CDP^{concentrated DP} 등 다양한 형태의 변형이 등장하였고, 최근에는 가설검정 형태에 기반한 Gaussian DP (혹은 $f$-DP)의 개념도 등장하였습니다. 이러한 시도들은 privacy loss에 대한 bound를 구성하는 과정을 좀 더 tight하게 만들기 위해 이루어졌고, 이번에 살펴볼 Renyi DP(RDP) 역시 DP의 변형된 정의 중 하나입니다. 참고한 논문은 Ilya Mironov의 Rényi Differential Privacy(2017) 와 Yuxiang Wang의 Subsampled Renyi Differential Privacy and Analytical Moments Accountant(2019) 입니다.

Variants of Differential Privacy

$\epsilon$-DP

Differential privacy는 데이터셋 $D$에 대해, 1개의 데이터 포인트에 의해 발생하는 정보 유출을 확률적으로 제한하는 것을 목표로 합니다. 가장 기본적인 형태는 $\epsilon$-DP로, 다음과 같이 정의됩니다.

\[\Pr(f(D)\in S) \le e^\epsilon \Pr(f(D')\in S)\]

여기서 $D$와 $D’$는 1개의 데이터 포인트만 다르고, $f$는 데이터셋 $D$에 대한 함수를 의미합니다 ($D\sim D’$ 와 같이 나타내기도 합니다). 이때 $f(D)$는 $D$에 대한 함수 $f$의 결과값을 의미하며, $S$는 $f$의 결과값이 속할 수 있는 집합(measurable set)을 의미합니다.

Laplace Mechanism

$\epsilon$-DP를 만족하는 대표적인 메커니즘은 Laplace 메커니즘입니다. Laplace 메커니즘은 $f(D)$에 대한 노이즈를 추가하는 방식으로, 다음과 같이 정의됩니다.

\[\mathbf{L}_\epsilon f(x) \triangleq f(x) + \text{Lap}\left(\frac{\Delta_1 f}{\epsilon}\right)\]

여기서 $\text{Lap}(\lambda)$는 평균이 0이고 scale이 $\lambda$인 Laplace 분포를 의미하며, $\Delta_1 f$는 $f$의 L1-민감도^sensitivity를 의미합니다. 민감도는 $f$의 결과값이 변할 수 있는 최대 변화량을 의미하며, 다음과 같이 정의됩니다.

\[\Delta_1 f = \max_{x\sim x'}\|f(x) - f(x')\|_1\]

$(\epsilon,\delta)$-DP

$(\epsilon,\delta)$-DP는 확률적인 형태로 $\epsilon$-DP를 만족하는 것을 의미합니다. 즉, $\delta$의 확률을 제외하고는 $\epsilon$-DP를 만족한다는 것을 의미합니다. $(\epsilon,\delta)$-DP는 다음과 같이 정의됩니다.

\[\Pr(f(D)\in S) \le e^\epsilon \Pr(f(D')\in S) + \delta\]

$\delta=0$인 경우는 $\epsilon$-DP와 동일하기 때문에 $\epsilon$-DP와 유사하다고 생각할 수 있지만, $\delta$의 존재로 인해 $\epsilon$-DP와 $(\epsilon,\delta)$-DP는 다른 성질을 가지게 됩니다.

Gaussian Mechanism

$(\epsilon,\delta)$-DP를 만족하는 대표적인 메커니즘은 Gaussian 메커니즘입니다. Gaussian 메커니즘은 $f(D)$에 대한 정규분포 노이즈를 추가하는 방식으로, 다음과 같이 정의됩니다.

\[\begin{align} \mathbf{G}_{\epsilon,\delta} f(x) &\triangleq f(x) + N(0,\sigma^2) \\ \sigma &> \sqrt{2\log(1.25/\delta)}\Delta_2 f/\epsilon \end{align}\]

$\Delta_2 f$는 $f$의 L2-민감도를 의미합니다. 주의할 것은, Gaussian mechanism은 $\epsilon$-DP를 만족하지 않는다는 것입니다. 또한, 일반적으로 가우시안 분포는 좋은 성질(ex. 두 가우시안 분포의 합은 가우시안 분포)을 가지기 때문에, Laplace mechanism보다 더 많이 사용되는 편입니다.

Concentrated Differential Privacy (CDP)

CDP는 2016년에 두 논문 (Bun & Steinke, 2016 : zCDP), (Dwork & Rothblum, 2016 : CDP) 에 의해 정립된 개념으로, subgaussian tail에 기반해 정의합니다. 여기서는 Dwork이 2016에 제안한 CDP에 대해 간략히 소개하겠습니다.

Subgaussian Random Variable

확률변수 $X$가 다음을 만족하면 이를 $\tau$-subgaussian ($\tau>0$) 인 확률변수라고 정의합니다.

\[\forall \lambda\in \mathbb{R}: \mathrm{E}[e^{\lambda X}] \le \exp \left(\frac{\lambda^{2}\tau^{2}}{2}\right)\]

이를 해석해보면 moment generating function(MGF)가 표준편차가 $\tau$인 정규분포의 MGF보다 항상 작거나 같음을 의미합니다. 또한, 다음과 같이 표준편차의 최소값으로서 subgassian standard $\tau(X)$를 정의합니다.

\[\tau(X) := \inf\lbrace \tau\ge 0 : X \text{ is }\tau-\text{subgaussian}\rbrace\]

Privacy Loss Random Variable

Support가 동일한 두 개의 이산확률변수 $Y,Z$가 주어졌을 때, privacy loss random variable $L_{(Y\Vert Z)}$은 다음과 같이 정의됩니다.

\[L_{(Y\Vert Z)} = \log \left(\frac{\Pr(Y=y)}{\Pr(Z=y)}\right),\quad y\sim Y\]

즉, 기댓값을 취하면 다음 관계가 성립합니다.

\[\mathrm{E}_{Y}\left[L_{(Y\Vert Z)}\right]=\mathrm{KL}(Y\Vert Z)\]

Subgaussian Divergence

두 확률변수 $Y,Z$에 대해 다음 두 조건을 만족하는 것을 $D_\mathrm{subG}(Y\Vert Z)\preceq (\mu,\tau)$ 라고 정의합니다.

1. $\mathrm{E}\left[L_{(Y\Vert Z)}\right]\le \mu$

2. 중심화^centered된 $L_{(Y\Vert Z)}- \mathrm{E}L_{(Y\Vert Z)}$ 가 subgaussian이고,

   \[\tau(L_{(Y\Vert Z)}- \mathrm{E}L_{(Y\Vert Z)})\le \tau\]

   가 성립한다.

$(\mu,\tau)$-CDP

Randomized algorithm $f$이 모든 이웃한 데이터셋 $D\sim D’$ 에 대해 $D_\mathrm{subG}(f(D) \Vert f(D’))\preceq (\mu,\tau)$ 이면 $(\mu,\tau)$-CDP 라고 정의합니다. 또한, $(\mu,\tau)$-CDP인 $f$에 대해서는 다음과 같은 성질이 성립합니다.

\[\Pr(L_{(Y\Vert Z)}\ge \mu+ t\cdot\tau) \le \exp \left(- \frac{t^{2}}{2}\right)\]

CDP나 zCDP는 모두 privacy loss variable $L_{(Y\Vert Z)}$ 을 설정하여, $L_{(Y\Vert Z)}$의 모든 moment^적률에 대한 bound를 가정합니다 (MGF 기반의 subgaussian 정의에 의함). 반면, 이후 살펴볼 RDP의 경우는 하나의 moment만을 이용한다는 차이가 있습니다. 우선 Renyi divergence^발산에 대해 다루어보도록 하겠습니다.

Renyi Divergence

Divergence는 두 확률측도(분포) 간의 거리를 재는 방식입니다. Rényi divergence는 이들 중 하나로, 두 확률분포 $P,Q$에 대한 $\alpha$-Renyi divergence는 다음과 같이 정의됩니다.

\[D_{\alpha}(P\Vert Q) \triangleq \frac{1}{\alpha-1}\log \mathrm{E}_{Q}\left(\frac{P(x)}{Q(x)}\right)^{\alpha} \tag{1}\]

$\alpha>1$ 로 주어지는데, $\alpha=1$일 경우는 극한을 취하여 얻을 수 있으며 이 경우 KL divergence와 동일한 것을 확인할 수 있습니다.

\[D_{1}(P\Vert Q) = \mathrm{E}_{P} \log \frac{P(x)}{Q(x)}\]

마찬가지로, $\alpha=\infty$ 인 경우는 다음과 같이 정의합니다.

\[D_{\infty}(P\Vert Q) = \sup_{x\in \mathrm{supp}(Q)}\log \frac{P(x)}{Q(x)}\]

$(\alpha,\epsilon)$-RDP

앞선 divergence 정의로부터, randomized mechanism $f$의 $\epsilon$-DP를 이끌어낼 수 있습니다. 만일 두 이웃한 데이터셋 $D\sim D’$ 에 대해

\[D_{\infty}(f(D)\Vert f(D')) \le \epsilon\]

을 만족한다면 $f$는 $\epsilon$-DP임이 확인가능합니다.

이에 착안하여, 다음과 같이 임의의 $\alpha>1$에 대한 DP를 고안할 수 있습니다. 이를 $(\alpha,\epsilon)$-RDP 라고 정의하며, 다음을 만족하는 randomized mechanism $f$를 의미합니다.

\[D_{\alpha}(f(D)\Vert f(D')) \le \epsilon\]

Properties

$(\alpha,\epsilon)$-RDP인 $f$에 대해 다음 성질들이 성립합니다.

Composition

\(f:\mathcal{D}\to \mathcal{R}_{1}\)이 \((\alpha,\epsilon_{1})\)-RDP이고 \(g:\mathcal{R}_{1}\times \mathcal{D}\to \mathcal{R}_{2}\) 가 \((\alpha,\epsilon_{2})\)-RDP 라고 하자. 그러면 $X\leftarrow f(D)$, $Y\leftarrow g(X,D)$ 로 정의되는 (결합) 메커니즘 $(X, Y)$은 \((\alpha,\epsilon_{1}+\epsilon_{2})\)-RDP를 만족한다.

RDP to $(\epsilon,\delta)$-DP

$f$가 $(\alpha,\epsilon)$-RDP를 만족하는 메커니즘이면 이는 동시에 $(\epsilon + \frac{\log 1/\delta}{\alpha-1},\delta)$-DP를 만족한다. ($\delta$는 0과 1사이 임의의 실수)

이외에도 여러 성질들이 존재하는데, 다음 표는 $\epsilon$-DP와 해당 성질들을 비교한 것입니다.

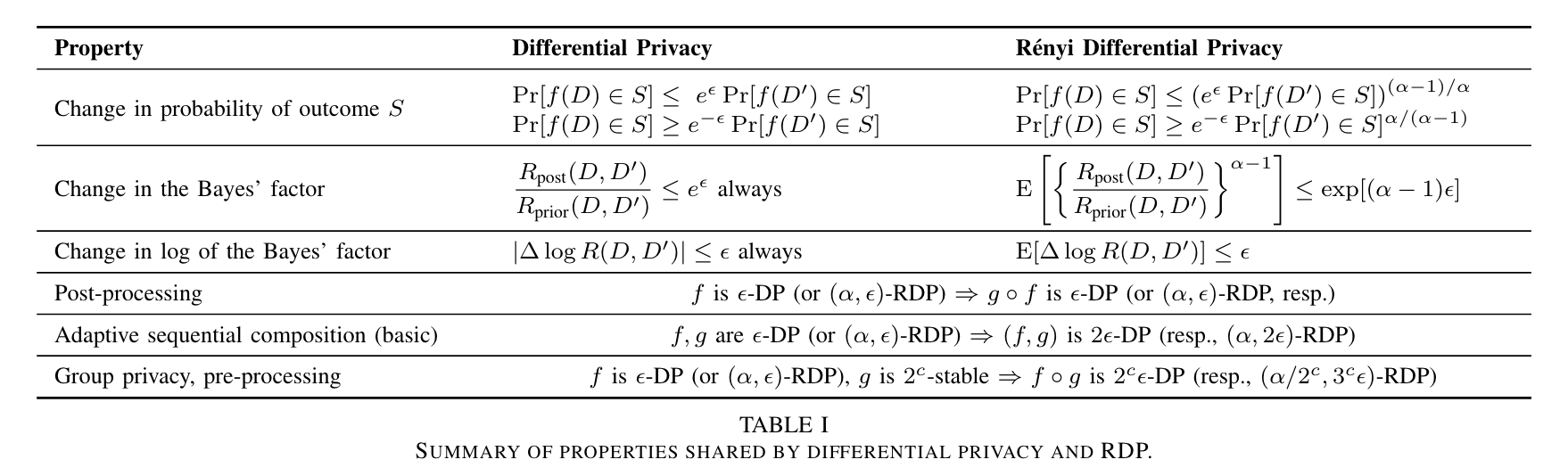Source: Ilya Mironov, “Rényi Differential Privacy,” (2017)

RDP and Moments Accountant

DP-SGD에서 사용한 moments accountant의 개념을 RDP에도 적용할 수 있습니다. Moments accountant 개념은 본질적으로 CGF^{Cumulative Generating Function}의 bound $\alpha_\mathcal{M}(\lambda)$를 이용하여 privacy loss의 bound를 구하는 방식입니다. 또한 이를 이용하면 초기 설정한 $\epsilon$으로부터 $\delta$를 계산하거나, 반대로 $\delta$로부터 $\epsilon$을 계산할 수도 있습니다. (자세한 내용은 여기를 참고하세요)

\[\begin{align} \delta\Rightarrow \epsilon:\quad &\epsilon(\delta)= \min_{\lambda}\frac{\log(1/\delta)+\alpha_\mathcal{M}(\lambda)}{\lambda}\\ \epsilon\Rightarrow \delta:\quad &\delta(\epsilon) =\min_{\lambda}\exp \left(\alpha_\mathcal{M}(\lambda)-\lambda\epsilon\right) \end{align}\]

(DP-SGD 포스트에서와의 통일성을 위해 randomized mechanism을 $\mathcal{M}$으로 표기했습니다.)

우선, $(\alpha,\epsilon)$-RDP에서 $\epsilon$을 $\alpha$의 함수로 볼 수 있습니다. 이를 나타내기 위해 $\epsilon_\mathcal{M}(\alpha)$ 로 표기하도록 하겠습니다. 그러면 RDP의 정의는 다음과 같이 다시 쓸 수 있습니다.

\[\sup_{D\sim D'} D_{\alpha}(\mathcal{M}(D)\Vert \mathcal{M}(D'))\le \epsilon_\mathcal{M}(\alpha)\]

이때, Renyi divergence의 정의로부터 다음 관계가 성립합니다.

\[\begin{align} \alpha_\mathcal{M}(\lambda:D,D') &= \log \mathrm{E}_{z\sim \mathcal{M}(D)} \left[\left(\frac{\mathcal{M}(D)(z)}{\mathcal{M}(D')(z)}\right)^{\lambda}\right]\\ &= \log \mathrm{E}_{z\sim \mathcal{M}(D')} \left[\left(\frac{\mathcal{M}(D)(z)}{\mathcal{M}(D')(z)}\right)^{\lambda+1}\right] \end{align}\]

여기서 $\alpha_\mathcal{M}(\lambda:D,D’)$ 는 privacy loss random variable $L$의 CGF를 의미합니다. 두번째 등식은 측도 변환으로부터 얻어집니다.

Moments accountant에서 DP와 moment bound가 동치임을 보였는데, 위 설정으로부터 RDP와 moment bound가 역시 동치임을 보일 수 있습니다. 이는 다음과 같이 주어집니다.

\[\text{Moment bound }\alpha_\mathcal{M}(\lambda) \Leftrightarrow \left(\lambda+1 ,\frac{\alpha_\mathcal{M}(\lambda)}{\lambda}\right)-\mathrm{RDP}\]

References

• I. Mironov, “Rényi Differential Privacy,” in 2017 IEEE 30th Computer Security Foundations Symposium (CSF), Santa Barbara, CA: IEEE, Aug. 2017, pp. 263–275. doi: 10.1109/CSF.2017.11.
• Y.-X. Wang, B. Balle, and S. P. Kasiviswanathan, “Subsampled Renyi Differential Privacy and Analytical Moments Accountant,” in Proceedings of the Twenty-Second International Conference on Artificial Intelligence and Statistics, PMLR, Apr. 2019, pp. 1226–1235. Accessed: May 13, 2024. [Online]. Available: https://proceedings.mlr.press/v89/wang19b.html
• M. Bun and T. Steinke, “Concentrated Differential Privacy: Simplifications, Extensions, and Lower Bounds.” arXiv, May 06, 2016. doi: 10.48550/arXiv.1605.02065.
• C. Dwork and G. N. Rothblum, “Concentrated Differential Privacy.” arXiv, Mar. 16, 2016. doi: 10.48550/arXiv.1603.01887.