Randomized Experiment

Randomized Experiment

Randomized Experiment, 혹은 Randomized Control Test(RCT)라고 부르는 실험 계획 방식은 일반적인 연구방법에 약간의 확률변수를 추가하여 인과추론을 가능하게끔 하는 실험 방식이다. 일반적인 관찰 연구에서는(ex. 의학/약학 연구) 실험군(treatment group)과 대조군(control group)을 나누기 위해 여러 샘플링 방법론 등을 사용한다(ex. Stratified sampling). 하지만 이러한 방식은 초기 실험 집단 설정에 많은 비용을 필요로하고, 결국 confounder를 완벽하게 제거하기는 어렵다는 문제가 있다. 따라서 이 문제를 해결하기 위해, 실험군을 설정하는 과정을 완전 랜덤으로 설정하는 방식을 고안했는데, 이것이 바로 RCT이다.

가장 간단한 예시는 동전 던지기를 생각하면 된다. 예를 들어 약물의 효과성을 검정하고자 할 때, 동전을 던져 앞면이 나오면 약물을 투여하고($T=1$), 뒷면이 나오면 약물을 투여하지 않는($T=0$) 방식을 생각해보자. 이 경우 약물 투여(treatment)는 오로지 확률이 0.5인 베르누이 독립시행에만 의존하므로, confounder의 영향을 받지 않게 된다. 또한, 이렇게 구성한 RCT에서는 association이 correlation이라는 성질이 존재한다. 즉, 상관관계를 파악하는 것 만으로도 인과관계를 검정할 수 있게 되는 효과가 존재한다는 것이다. 이에 대해서는 아래의 세 가지 관점으로 증명할 수 있다.

Covariate Balance

Definiton

실험군과 무관하게, 공변량(covariate)들의 확률분포가 동일하다면 이를 covariate balance가 존재한다고 표현한다. 즉,

\[P(X\vert T=1)\overset{d}{=}P(X|T=0)\]

이다.

RCT에서는 실험군의 선택이 공변량과 독립인 확률분포(ex. 베르누이 독립 시행)로부터 얻어지므로, 결국 다음과 같다.

\[P(X|T=1)=P(X)\quad \mathrm{and} \quad P(X|T=0)=P(X)\]

즉, RCT에서는 covariate balance가 존재한다는 것을 의미한다.

그렇다면, covariate balanace가 존재하는 경우 연관관계가 인과관계가 될 수 있음을 파악해야 하는데, 이는 다음과 같이 증명할 수 있다.

Proof

집합 $X$를 모든 조절효과의 집합이라고 하자(관측되지 않은 조절효과들도 포함한다). 이때 조절효과란 종속변수와 독립변수의 관계에 영향을 미칠 수 있는 모든 변수를 의미한다. 연관관계가 인과관계임을 보이기 위해서는 다음 관계를 보이는 것으로 충분하다.

\[P(y|do(t))=P(y|t)\]

이때, 다음이 성립한다. 이를 backdoor adjustment라고도 한다.

\[\begin{aligned} P(y|do(t))&= \sum_{x\in X}P(y|do(t),x)P(x|do(t))\\ &= \sum_{x\in X} P(y|t,x)P(x|do(t))\\ &= \sum_{x\in X} P(y|t,x)P(x) \end{aligned}\]

이로부터 다음과 같이 유도해나갈 수 있다.

\[\begin{align} &= \sum_{x}\frac{P(y|t,x)P(t|x)P(x)}{P(t|x)}\\ &= \sum_{x}\frac{P(y,t,x)}{P(t|x)}\\ &= \sum_{x}\frac{P(y,t,x)}{P(t)}\tag{a}\\ &= \sum_{x}P(y,x|t)\\ &= P(y|t) \end{align}\]

(a) 유도과정은 $X\perp T$ 로부터 얻어진다(RCT assumption).

Exchangeability

RCT에서는 실험군과 대조군 간의 교환가능성(exchangeability)이 존재한다. 즉, 실험군과 대조군을 바꿔도 전체 실험 결과에는 영향을 주지 못하는데, 애초에 동전 던지기와 같은 독립 확률변수로부터 실험군을 설정하였으므로 동전의 앞면 뒷면의 의미만 바꾸는 것은 실험 자체에 영향을 미치지 못한다. 이러한 교환가능성 개념으로부터도 다음과 같이 연관관계가 인과관계임을 보일 수 있다.

Proof

우선, 교환가능성은 다음과 같이 나타낼 수 있다.

\[\begin{align} \mathbb{E}[Y(1)|T=1] = \mathbb{E}[Y(1)|T=0]\tag{1} \\ \mathbb{E}[Y(0)|T=1] = \mathbb{E}[Y(0)|T=0]\tag{2} \end{align}\]

식 (1)에서는 실험군($T=1$)과 대조군($T=0$)이 바뀌어도 실험 결과가 $Y=1$ 인 것에 영향을 주지 못한다는 것을, 식 (2)에서는 다른 실험 결과에서의 교환 가능성을 의미한다. 이때, 실험 참가 대상이 실험군과 대조군에 포함될 확률은 모두 $0.5$로 같으므로, 다음이 성립한다.

\[\begin{align} \mathbb{E}Y(1)=\mathbb{E}[Y(1)|T=1] = \mathbb{E}[Y(1)|T=0] \\ \mathbb{E}Y(0)=\mathbb{E}[Y(0)|T=1] = \mathbb{E}[Y(0)|T=0] \end{align}\]

따라서, 다음 결과를 얻을 수 있다.

\[\begin{aligned} \mathbb{E}Y(1)-\mathbb{E}Y(0)&= \mathbb{E}[Y(1)|T=1]-\mathbb{E}[Y(0)|T=0]\\ &= \mathbb{E}[Y|T=1]=\mathbb{E}[Y|T=0] \end{aligned}\]

No Backdoor Paths

만일 confounder $X$가 존재하여 $T\leftarrow X\rightarrow Y$ 의 backdoor path가 존재하면 인과관계의 파악이 어려운 문제가 존재한다. (아래)

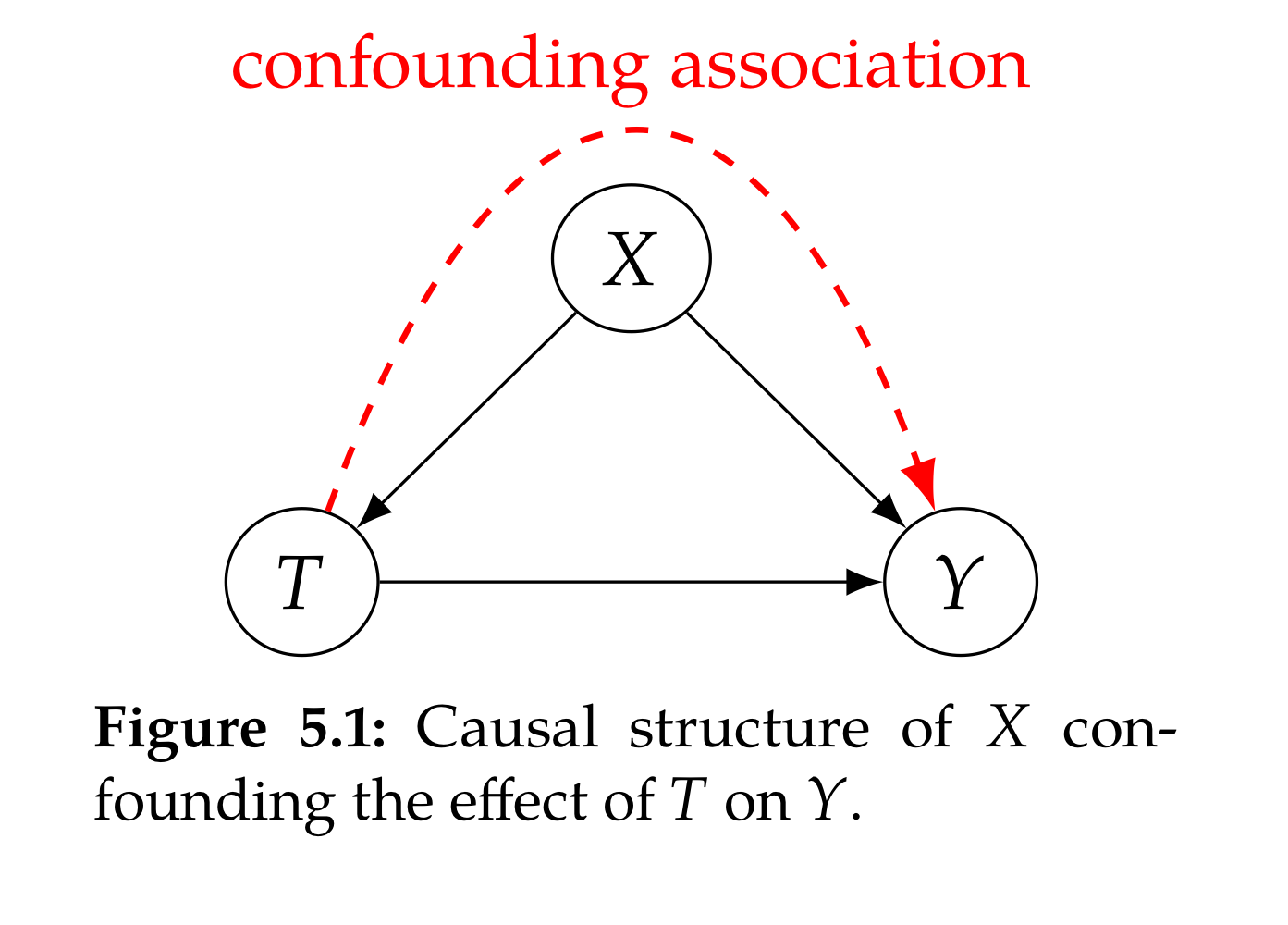
RCT를 이용하면 처치효과에 confounder 영향을 배제할 수 있으므로, 결국 $Y$에 미치는 $T$의 영향을 측정하기만 한다면 이러한 연관관계를 이용해 인과관계를 설정할 수 있다(아래).

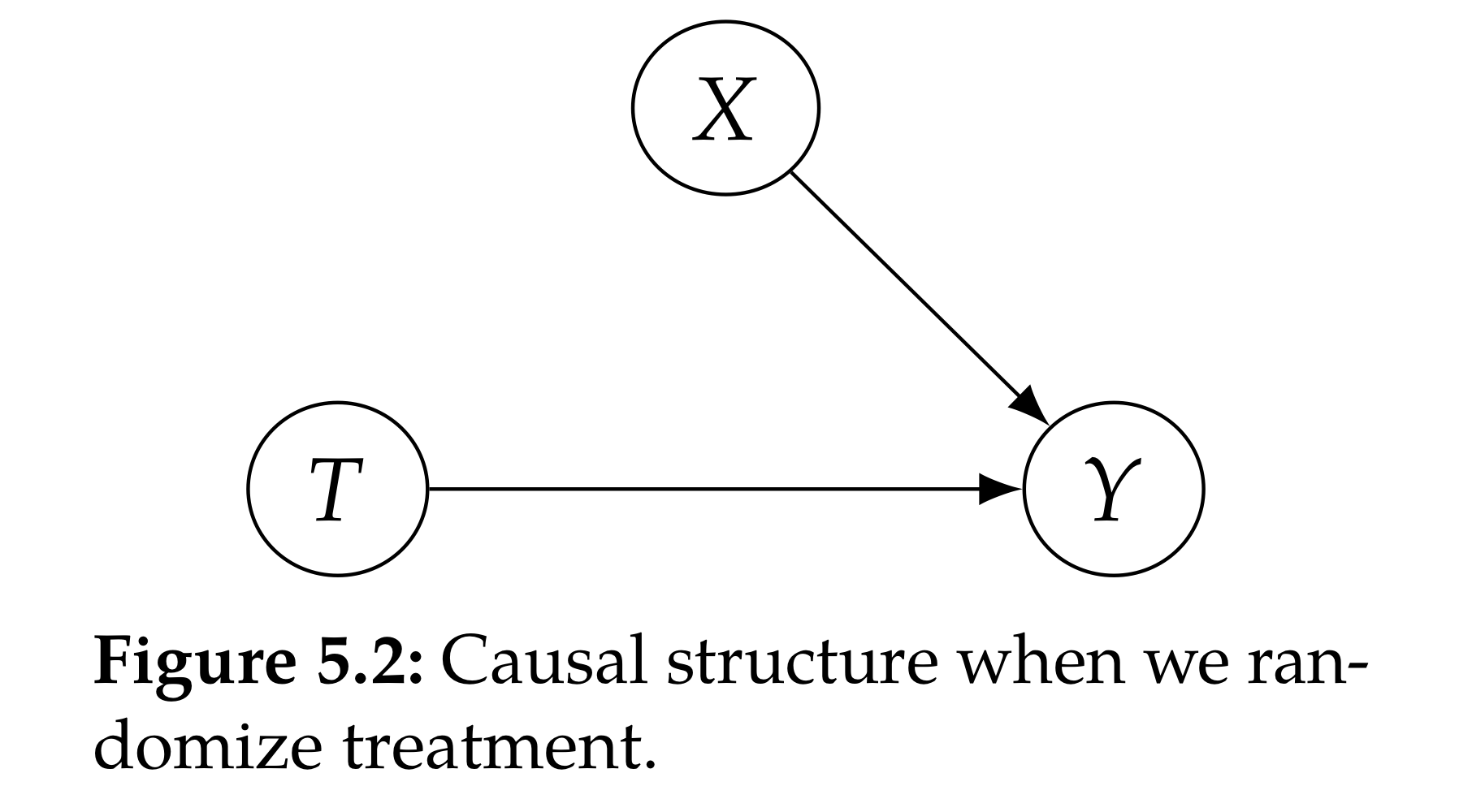
References

• Brady Neal - Introduction to Causal Inference