최근 Mamba (Gu & Dao, 2024)의 등장으로 상태공간모형(State-Space Model, 이하 SSM)은 Transformer를 대체할 수 있는 아키텍처의 후보로 여겨지고 있습니다. 이번 글에서는 보다 일반적인 상태공간모형과, 이를 딥러닝에 적용한 S4, HiPPO 등의 아키텍쳐에 대해 다루어보도록 하겠습니다.

State Space Model

Revisit: State Space Model in Time Series Analysis

통계학에서 다루는 상태공간모형(State-Space Model, 이하 SSM)은 일반적인 SSM을 불연속적인 Markov chain으로 변환한 것으로, 관측가능한 데이터 \(\mathbf{y}_{t}, \mathbf{x}_{t}\) 와 hidden state data \(\mathbf{h}_{t}\) 가 결합된 모델입니다. 이를 수식으로 나타내면 다음과 같습니다.

\[\begin{cases} \mathbf{h}_{t} = \Phi\mathbf{h}_{t-1}+\gamma \mathbf{x}_{t}+w_{t}\\ \mathbf{y}_{t} = A_{t}\mathbf{h}_{t}+\Gamma\mathbf{x}_{t}+ v_{t} \end{cases}\]

이때 noise vector $w_{t}, v_{t}$ 는 각각 정규분포 $N_{p}(0,Q), N_q(0,R)$ 을 따르며 각각 독립이라는 가정이 필요합니다. 이러한 정규성 가정(Gaussian assumption)은 상태공간모형에서 매우 중요합니다. 이렇게 주어지는 상태공간모형은 Kalman Filter로 hidden state를 추정할 수 있습니다.

시퀀스로 주어지는 hidden state $\mathbf{h}_t$ 를 사용한다는 점에서 위 구조는 다음과 같이 주어지는 RNNRecurrent Neural Network과 유사한 구조를 가지고 있습니다 (Elman network).

\[\begin{aligned} \mathbf{h}_t &= \sigma_h(\mathbf{W}_h\mathbf{x}_t + \mathbf{U}_h\mathbf{h}_{t-1} + \mathbf{b}_h)\\ \mathbf{y}_t &= \sigma_y(\mathbf{W}_y\mathbf{h}_t + \mathbf{b}_y) \end{aligned}\]

State Space Model

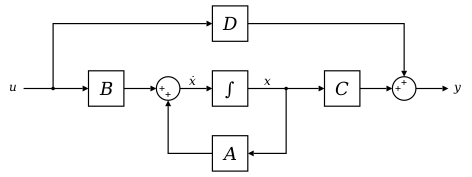SSM representation. Source: wikipedia

앞서 다룬 시계열 데이터 분석에서의 SSM은 discrete-time 상태공간모형입니다. 일반적인 형태의 상태공간모형은 continuous-time SSM 으로, 이는 다음과 같이 미분방정식 형태로 주어집니다.

\[\begin{cases} \dot{\mathbf{x}}(t) = A\mathbf{x}(t) + B\mathbf{u}(t)\\ \mathbf{y}(t) = C\mathbf{x}(t) + D\mathbf{u}(t) \end{cases}\]

이때, $\mathbf{x}(t)$ 는 hidden state, $\mathbf{u}(t)$ 는 control input, $\mathbf{y}(t)$ 는 observation을 나타냅니다.

딥러닝 모델들에서 다루는 SSM은 두번째 식인 output의 출력 과정을 간단하게 변형한 형태로 주어집니다.

\[\begin{cases} \dot{\mathbf{x}}(t) = \mathbf{A}\mathbf{x}(t) + \mathbf{B}\mathbf{u}(t)\\ \mathbf{y}(t) = \mathbf{C}\mathbf{x}(t) \end{cases}\]

위 미분방정식의 해는 variation of parameters를 사용하여 다음과 같이 계산됩니다.

\[\mathbf{x}(t) = e^{At}\mathbf{x}(0) + \int_{0}^{t}e^{A(t-\tau)}\mathbf{B}\mathbf{u}(\tau)d\tau\]

Discretization

실제로 위 SSM을 딥러닝 모델로 구현할 때에는, continuous-time SSM을 discrete-time SSM으로 변환하여 사용해야 합니다. 이러한 과정을 discretization 이라고 하는데 (아래 그림 참고), 이를 통해 continuous-time SSM을 RNN과 같은 구조로 변환하여 사용할 수 있습니다.

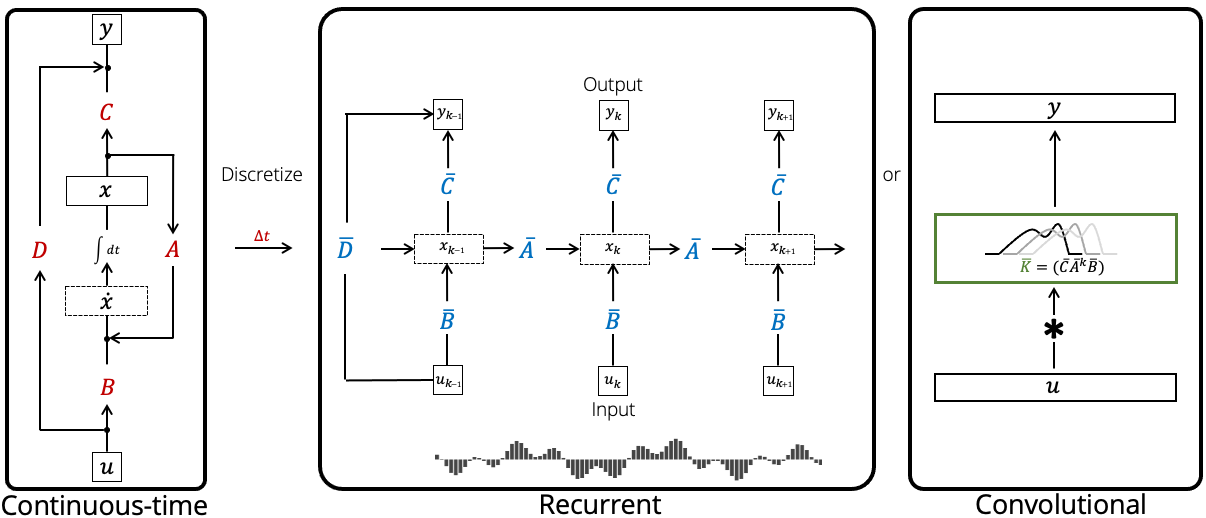Source: https://hazyresearch.stanford.edu/blog/2022-01-14-s4-3

임의의 $t\ge 0, \Delta t >0$ 에 대해 다음 미분방정식

\[\dot{\mathbf{x}}(t) = A\mathbf{x}(t) + B\mathbf{u}(t)\]

의 해는 다음을 만족합니다.

\[\mathbf{x}(t+\Delta t) = \mathbf{x}(t) + \int_{t}^{t+\Delta t}A\mathbf{x}(\tau)d\tau + \int_{t}^{t+\Delta t}B\mathbf{u}(\tau)d\tau\]

이때 적분을 근사하기 위해 다음과 같은 방법들이 사용됩니다.

  • Forward Euler discretization:

    \[\mathbf{x}(t+\Delta t) \approx (I+\Delta tA)\mathbf{x}(t) + \Delta tB\mathbf{u}(t)\]

  • Backward Euler discretization:

    \[\mathbf{x}(t+\Delta t) \approx (I-\Delta tA)^{-1}\mathbf{x}(t) + \Delta t(I-\Delta tA)^{-1}B\mathbf{u}(t)\]

  • Bilinear discretization:

    \[\mathbf{x}(t+\Delta t) \approx \left(I-\frac{\Delta t}{2}A\right)^{-1}\left(I+\frac{\Delta t}{2}A\right)\mathbf{x}(t) + \Delta t\left(I-\frac{\Delta t}{2}A\right)^{-1}B\mathbf{u}(t)\]

  • Generalized bilinear discretization: For $\alpha\in(0,1)$,

    \[\mathbf{x}(t+\Delta t) \approx \left(I-\alpha\Delta tA\right)^{-1}\left(I+(1-\alpha)\Delta tA\right)\mathbf{x}(t) + \Delta t\left(I-\alpha\Delta tA\right)^{-1}B\mathbf{u}(t)\]

HiPPO

우선 현재 사용되는 SSM 모델의 근간이 되는 HiPPO (Gu et al., 2020) 에 대해 알아보도록 하겠습니다. HiPPO는 High-order Polynomial Projection Operator의 약자로, RNN의 단점을 극복하기 위해 제안된 모델입니다.

현재 사용되는 언어 모델의 de facto standard는 Transformer 입니다. Transformer의 등장 이전에는 RNN(Recurrent Neural Network)이 그 역할을 수행하였는데, RNN은 데이터를 순차적으로 처리하는 특성상 병렬화가 어렵다는 단점이 있었습니다.

또한, LSTM과 같은 RNN 구조는 sequence 정보를 보존하긴 하지만, 긴 시퀀스에 대한 정보를 잘 보존하지 못한다는 단점이 있습니다. 다만, RNN 구조는 시퀀스 생성에서는 계산 비용 측면에서 transformer에 비해 큰 장점을 갖습니다. Generation cost가 시퀀스 길이에 선형적으로 증가하기 때문입니다 ($O(n)$).

HiPPO는 이러한 RNN의 장점을 유지하면서, 시퀀스 정보에 대한 기억(memory) 문제를 해결하기 위해 제안된 구조입니다.

Memory Units

Memory 문제를 해결하기 위해, HiPPO는 memory units라는 개념을 이용합니다. 이는 Voelker et al. (2019) 에서 제안된 것으로, memory unit $c(t)$은 input sequence $f_{\le t}={f(\tau)}_{\tau\in[0,t]}$ 에 대한 정보를 저장합니다. 이때 memomry unit $c(t)$ (혹은 discrete 관점에서 $c_l$) 가 좋은 memomry를 갖는다는 것은, 다음 reconstruction mechanism

\[c(t) \mapsto \hat{f}_{\le t}\]

가 존재하여 \(\hat{f}_{\le t} \approx f_{\le t}\) 가 성립한다는 것을 의미합니다. 이를 위해 HiPPO에서는 $c(t)\in \mathbb{R}^N$ 을 다항함수의 계수로 사용하여, 다음과 같은 reconstruction mechanism $g$로 $f_{\le t}$ 를 다항함수로 근사합니다.

\[g^{(t)}(x) = \sum_{i=0}^{N-1}c_i(t)P_i^{(t)}(x)\]

이때, basis function $P_i^{(t)}(x)$ 는 $t$ 시점의 $i$차 다항함수를 나타냅니다. 구체적으로는, $[0,t]$에서 정의되는 time-varying measure $\mu^{(t)}$ 를 사용하여

\[\Vert f_{\le t} - g^{(t)} \Vert_{\mu^{(t)}}\]

를 최소화하는 $c(t)$ 를 찾습니다. 이를 위해 각 다항계수 $c_i(t)$ 는 다음과 같이 계산됩니다.

\[\begin{aligned} c_i(t) &= \langle f, P_i^{(t)} \rangle_{\mu^{(t)}} \\ &= \int_0^t f(x)P_i^{(t)}(x)d\mu^{(t)}(x) \\ &= \int_0^t f(x)P_i^{(t)}(x) \omega(t,x) dx \end{aligned}\]

여기서 $\omega(t,x)$ 는 measure $\mu^{(t)}$ 에 대응하는 weight function 입니다.

매 step $t$마다 위 식을 통해 $c(t)$ 를 계산하는 것은 계산 비용이 매우 큽니다. 그러나 HiPPO 논문에서는 $c(t)$가 다음과 같은 ODE를 따른다는 것을 보였습니다.

\[\dot{c}(t) = \mathbf{A}(t)c(t) + \mathbf{B}(t)f(t)\]

이때, $\mathbf{A}(t), \mathbf{B}(t)$ 는 각각 $N\times N, N\times 1$ 행렬로, measure $\mu^{(t)}$ 에 따라 계산됩니다. HiPPO 논문에서는 두 가지 measure에 대해 각각 다음과 같은 ODE를 제안하였습니다.

HiPPO-LegT

첫 번째 경우는 최근 $\tau$ 시점들에 대한 uniform measure

\[\omega(t,x) = \frac{1}{\tau}\mathbf{1}_{[t-\tau,t]}(x)\]

와 다음과 같이 정의되는 Legendre polynomial basis

\[\begin{aligned} &P_0(x) = 1\\ &P_1(x) = x\\ &(1-x^2)P_n''(x) - 2xP_n'(x) + n(n+1)P_n(x) = 0 \end{aligned}\]

를 사용한 경우로, Translated Legendre Measure 라고 부릅니다. 이때, memory unit에 대한 ODE는 다음과 같습니다.

\[\begin{aligned} &\dot{c}(t) = -\frac{1}{\tau}Ac(t) + \frac{1}{\tau}Bf(t),\quad c(0) = 0\\ &A_{nk} = (2n+1)^{\frac{1}{2}}(2k+1)^{\frac{1}{2}}\begin{cases} 1 & \text{if } k\le n\\ (-1)^{n-k} & \text{if } k \ge n \end{cases}\\ &B_n = (2n+1)^{\frac{1}{2}} \end{aligned}\]

Uniform measure를 사용한다는 것은, 이전 시점들에 대해 동일한 가중치를 부여한다는 것을 의미합니다 (아래 그림의 왼쪽).

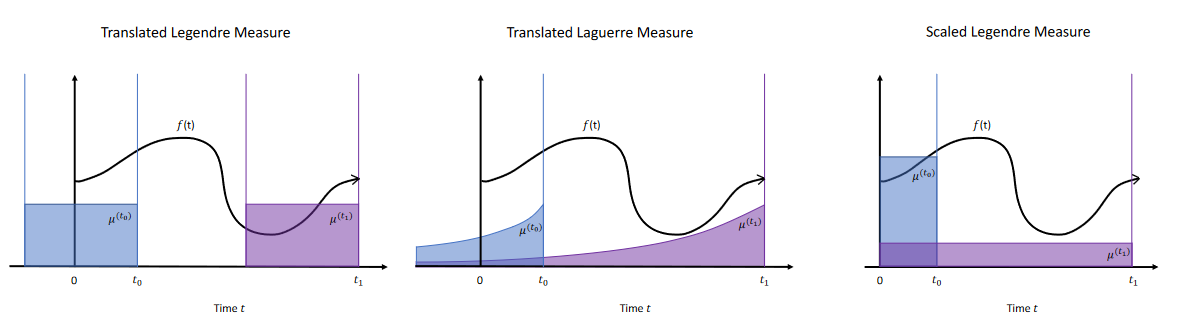Source: Gu et al. (2020)

HiPPO-LagT

Translated Laguerre measure는 Laguerre polynomial basis와 exponential weight function을 사용하는 경우입니다. 이때, weight function은 다음과 같이 주어집니다.

\[\omega(t,x) = (t-x)^\alpha e^{-(t-x)} \mathbb{I}_{(-\infty,t)}(x)\]

이는 최근 시점들에 대해 더 높은 가중치를 부여하는 것으로 볼 수 있습니다 (위 그림의 가운데 참고). 이때, memory unit에 대한 ODE는 다음과 같습니다.

\[\begin{aligned} \dot{c}(t) &= -Ac(t) + Bf(t),\quad c(0) = 0\\ A_{nk} &= \begin{cases} 1 & \text{if } n \ge k\\ 0 & \text{if } n < k \end{cases}\\ B_n &= 1 \end{aligned}\]

HiPPO-LegS

마지막으로, Scaled Legendre measure는 이전까지의 전 시점에 대해 uniform weight을 부여하는 측도입니다.

\[\omega(t,x) = \frac{1}{t} \mathbb{I}_{[0,t]}(x)\]

이에 대한 memory unit ODE는 다음과 같습니다.

\[\begin{aligned} \dot{c}(t) &= -\frac{1}{t}Ac(t) + \frac{1}{t}Bf(t),\quad c(0) = 0\\ A_{nk} &= \begin{cases} (2n+1)^{\frac{1}{2}}(2k+1)^{\frac{1}{2}} & \text{if } n>k\\ n+1 & \text{if } n = k\\ 0 & \text{if } n < k \end{cases}\\ B_n &= (2n+1)^{\frac{1}{2}} \end{aligned}\]

Discrete-time SSM

Memory-unit ODE를 풀기 위해, 위 ODE를 discrete-time으로 변환하여 사용합니다. 예를 들어 Hippo-LegS (scaled Legendre measure)에 대해 forward Euler discretization을 사용하면 다음과 같이 주어집니다.

\[\begin{aligned} c((k+1)\Delta t) - c(k\Delta t) &= -\frac{\Delta t}{\Delta tk}Ac(k\Delta t) + \frac{\Delta t}{\Delta tk}Bf_k\\ c((k+1)\Delta t) &= (I-\frac{1}{k}A) c(k\Delta t) + \frac{1}{k}Bf_k \\ &\triangleq \bar A_k c_k + \bar B_k f_k \end{aligned} \tag{1}\]

이러한 방식으로 SSM을 RNN과 유사한 구조로 변환하여 사용할 수 있습니다. 그러나 이 역시 RNN과 마찬가지로 병렬 연산이 불가능하기 때문에, 이를 해결하고자 S4 모델에서는 convolution representation을 사용합니다.

LSSL and S4

Linear State-Space Layer

앞선 내용들에서는 memory unit을 기반으로 상태공간모형을 정의하였고, 이를 discretize할 경우 식 $(1)$과 같은 꼴로 표현된다는 것을 확인할 수 있었습니다. 이러한 linear dynamic system으로부터, input sequence \(\{u(t)\}_{t\in[0,T]}\) 를 받아 output sequence \(\{y(t)\}_{t\in[0,T]}\) 를 도출하는 seq2seq 형태의 레이어를 구성할 수 있습니다. 이러한 레이어를 Linear State-Space LayerLSSL 이라고 부릅니다.

\[\begin{align} \dot x(t) &= Ax(t) + Bu(t) \in \mathbb{R}^{n}\\ y(t) &= Cx(t) \in \mathbb{R} \end{align} \tag{LSSL}\]

위 미분방정식을 초기값 조건 $x(0)=\mathbf{0}\in \mathbb{R}^{n}$ 에 대해 풀면

\[y(t) = \int_{-\infty}^{\infty}K(t-s)u(s)ds = (K\ast u)(t)\]

를 얻게 되고, 여기서 $K,u$는 다음과 같이 정의됩니다.

\[\begin{aligned} K(t) &= \begin{cases} Ce^{tA}B&\text{for } t \ge 0\\ 0 & \text{otherwise} \end{cases}\\ u(t) &= \begin{cases} u(t)\ge 0 & \text{for }t \ge 0\\ 0&\text{otherwise} \end{cases} \end{aligned}\]

이렇게 정의되는 seq2seq layer를 continuous-time LSSL 이라고 합니다.

Initialization

위와 같이 정의되는 $(\mathrm{LSSL})$ 을 실제로 사용하기 위해서는 초기값 설정 문제가 매우 중요합니다. 일반적으로 행렬 $A$는 HiPPO-LegS를 사용하여 다음과 같이 초기화합니다.

\[A_{nk}= \begin{cases} (2n+1)^{\frac{1}{2}}(2k+1)^{\frac{1}{2}} & \text{if } n>k\\ n+1 & \text{if } n = k\\ 0 & \text{if } n < k \end{cases}\]

이때 중요한 점은, 행렬 $A$가 time-invariant 하다는 것입니다. 이는 time-varying한 행렬 $A(t)$ 를 사용하는 HiPPO와의 차이점입니다. 또한, $B$는 랜덤한 초기값을 사용합니다.

Discrete-time LSSL

HiPPO에서 살펴본 것과 마찬가지로 위 $(\mathrm{LSSL})$ 을 discrete-time으로 변환하여 사용할 수 있습니다. 즉 다음과 같은 형태가 됩니다.

\[\begin{cases} x_k = \bar A x_{k-1} + \bar B u_k \\ y_k = C x_k \end{cases} \tag{2}\]

식 $(1)$ 의 형태로 주어지는 discretized SSM을 다시 살펴보도록 하겠습니다. Discretized SSM은 다음과 같이 주어집니다. (Notation을 변경하였습니다)

여기서 $x_{-1}=0$ 으로 두고 위 식을 계속해서 전개하면 다음과 같은 표현이 가능합니다.

\[\begin{aligned} y_k &= C \bar A^k \bar B u_0 + C \bar A^{k-1} \bar B u_1 + \cdots + C \bar A \bar B u_{k-1} + C \bar B u_k \\ y &= \overline{\mathbf{K}} \ast u \end{aligned}\]

이때, $\overline{\mathbf{K}}$ 는 다음과 같이 주어집니다.

\[\begin{aligned} \overline{\mathbf{K}} &\triangleq \mathcal{K}_L(\bar A, \bar B, C) \\ &:= \begin{pmatrix} C \bar B & C \bar A \bar B & \cdots & C \bar A^{L-1} \bar B \end{pmatrix} \end{aligned}\]

즉, SSM의 연산과정은 하나의 convolution 연산으로 표현할 수 있고 이로 인해 FFT와 같은 효율적인 연산이 가능해집니다. 이렇게 정의되는 $\overline{\mathbf{K}}$ 를 SSM convolution kernel 이라고 부릅니다.

S4 Model

Discretized SSM (식 $(2)$)을 계산하는 것은 $L$번의 반복된 행렬곱 연산을 필요로 합니다. 즉, $O(N^2L)$ 번의 연산과 $O(NL)$ 만큼의 메모리가 요구됩니다. 이를 해결하기 위해 S4에서는 행렬 $A$를 대각화하여 다음과 같이 표현합니다.

Theorem

앞서 제시된 HiPPO ODE (그 종류에 관계 없이)에서의 행렬 $A$는 다음과 같이 나타낼 수 있습니다.

\[A = V\Lambda V^\ast - PQ^\top = V(\Lambda - (V^\ast P)(V^\ast Q)^\ast)V^\ast\]

여기서 $V$ 는 unitary matrix, $\Lambda$ 는 diagonal matrix, $P,Q$ 는 low-rank factorization을 나타냅니다 (rank $r$). 이러한 형태를 Normal Plus Low-Rank (NPLR) 이라고 합니다.

그러나 위 정리를 이용해도 $A$의 거듭제곱을 구하는 것은 느리다는 문제가 있습니다. 이를 해결하기 위해 S4에서는 다음과 같은 알고리즘을 제시합니다.

S4 Algorithm

  1. SSM generating function(SSMGF) 을 길이 $L$까지 계산합니다.

    \[\tilde C \leftarrow \left(\mathbf{I}- \bar A^{L}\right)^{\ast}\bar C\]

    여기서 SSM generating function은 다음과 같은 다항전개 형태를 말합니다.

    \[\sum_{k=0}^{\infty} \overline{\mathbf{K}}_k z^k\]

    ($z$ is root of unity단위근 : $z = e^{2\pi i/L}$)

  2. Black-box Cauchy kernel

    \[\begin{bmatrix} k_{00}(\omega) & k_{01}(\omega) \\ k_{10}(\omega) & k_{11}(\omega) \end{bmatrix} \leftarrow \begin{bmatrix} \tilde C & Q \end{bmatrix}^\ast \left(\frac{2}{\Delta}\cdot \frac{1-\omega}{1+\omega}-\Lambda\right)^{-1} \begin{bmatrix} B & P \end{bmatrix}\]

  3. Woodbury identity

    \[\hat{\mathbf{K}} \leftarrow \frac{2}{1+\omega}[k_{00}(\omega) - k_{01}(\omega)(1+k_{11}(\omega))^{-1}k_{10}(\omega)]\]

  4. Evaluate SSMGF at $z \in \Omega_L$

    \[\hat{\mathbf{K}}_k = \{\hat{\mathbf{K}}(\omega): \omega = \exp(2\pi i k/L)\}\]

  5. Inverse FFT

    \[\overline{\mathbf{K}} = \text{IFFT}(\hat{\mathbf{K}})\]

위와 같이 S4 모델은 Linear State-Space Layer를 효율적으로 계산하기 위한 방법을 제시하고 있습니다. 파라미터 수, 계산 비용 등에서 기존의 Attention mechanism을 사용하는 Transformer 아키텍쳐에 비해 효율적인 구조를 가지고 있다는 것이 S4의 장점입니다. (아래 표 참고)

Source: Gu et al. (2022)

여기서 $L$은 sequence length, $B$는 batch size, $H$는 hidden state의 차원을 나타냅니다. 저자는 S4 모델이 Convolution 연산과 Recurrence 연산의 장점만을 취한 형태로 볼 수 있다고 설명합니다.

References

Leave a comment