Spatio-Temporal Graph Convolutional Networks

Graph Convolutional Network는 Graph Neural Network의 가장 대표적인 모델 중 하나입니다. Graph Neural Network는 그래프 구조를 이용하여 노드의 특성을 업데이트하는 방법으로, 최근에는 다양한 분야에 적용되고 있습니다.

이번 글에서는 Graph Convolutional Network (GCN) 과 이를 시공간 데이터에 적용한 Spatio-Temporal Graph Convolutional Networks (STGCN), 그리고 이에 Attention Mechanism을 추가한 Attention Based Spatial-Temporal Graph Convolutional Networks (ASTGCN) 에 대해 알아보겠습니다.

Graph Convolutional Network (GCN)

우선, GCN에 대해 살펴보도록 하겠습니다. GCN은 2017년에 Kipf와 Welling에 의해 제안된 논문에서 처음 소개되었습니다. GCN은 그래프 구조를 이용하여 노드의 특성을 업데이트하는 방법입니다.

$N$개의 노드로 구성된 Graph $G = (V, E)$ (여기서 $V$는 노드 집합, $E$는 엣지 집합) 가 주어졌을 때, graph Laplacian $L$은 다음과 같이 정의됩니다.

\[L = D - A\]

여기서 $D$는 degree matrix로, $D_{ii} = \sum_j A_{ij}$ 입니다. $A$는 adjacency matrix^인접행렬로, $A_{ij} = 1$이면 노드 $i$와 $j$ 사이에 엣지가 존재함(connected)을 의미합니다. GCN은 이러한 그래프 구조를 이용하여 노드의 특성을 업데이트하는 방법입니다. 노드 $i$의 특성을 $X_i$라고 할 때, GCN은 다음과 같이 노드의 특성을 업데이트합니다. (여기서 특성이란 노드에 대응하는 변수들을 의미합니다.)

\[H^{(l+1)} = \sigma(\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}H^{(l)}W^{(l)}) \tag{1}\]

여기서 $H^{(l)}$는 $l$번째 레이어의 노드 특성을 의미하며, $\tilde{A} = A + I$는 self-loop를 추가한 adjacency matrix입니다. $\tilde{D}$는 $\tilde{A}$에 대응하는 degree matrix입니다. $W^{(l)}$는 $l$번째 레이어의 가중치 행렬이며, $\sigma$는 활성화 함수(ReLU)입니다. 이러한 방식으로 GCN은 그래프 구조를 이용하여 노드의 특성을 업데이트합니다.

Spectral Graph Convolution

위 식 $(1)$이 도출되는 과정은 spectral graph convolution이라는 연산을 이용하여 설명할 수 있습니다. Spectral graph convolution은 그래프 신호를 Fourier domain에서 다루는 방법입니다.

각 노드에 대해 스칼라 값으로 이루어진 신호 $x \in \mathbb{R}^N$가 주어졌을 때, filter(혹은 kernel) $g_\theta$ 에 대한 graph convolution operator $\ast_G$ 는 다음과 같이 정의됩니다.

\[g_\theta \ast_G x = U g_\theta U^Tx \tag{2}\]

여기서 $U$는 그래프 $G$의 normalized graph Laplacian $L = I - D^{-\frac{1}{2}}AD^{-\frac{1}{2}} = U\Lambda U^\top$의 eigenvector로 이루어진 행렬입니다. $g_\theta$는 $L$의 eigenvalue에 대응하는 filter로, $g_\theta = \text{diag}(\theta)$ 입니다. 이러한 방식으로 spectral graph convolution은 그래프의 eigenvector를 이용하여 노드의 특성을 업데이트합니다.

Chebyshev Polynomial Approximation

다만, 식 $(2)$는 계산량이 매우 크다는 문제점이 있습니다 ($O(N^2)$). 이를 해결하기 위해 Kipf와 Welling은 Chebyshev polynomial approximation을 이용하여 spectral graph convolution을 근사하는 방법을 제안했습니다. 이는 다음과 같이 정의됩니다.

\[g_{\theta'}(\Lambda) \approx \sum_{k=0}^K \theta_k T_k(\tilde{\Lambda}) \tag{3}\]

즉, kernel $g_{\theta’}$ 를 $K$차까지의 Chebyshev polynomial $T_k$ 로 근사하는 것입니다. Chebyshev polynomial은 다음과 같이 재귀적으로 정의됩니다.

\[\begin{aligned} T_0(x) &= 1 \\ T_1(x) &= x \\ T_{k+1}(x) &= 2xT_k(x) - T_{k-1}(x) \end{aligned}\]

이를 이용하면, graph convolution operator는 다음과 같이 근사될 수 있습니다.

\[g_{\theta'} \ast_G x \approx \sum_{k=0}^K \theta_k T_k(\tilde{L})x \tag{4}\]

여기서 $\tilde{L} = 2L/\lambda_{\max} - I$는 normalized graph Laplacian $L$을 이용하여 정의한 것입니다. 이러한 방식의 근사는, 계산 비용을 $O(\vert E\vert )$로 줄일 수 있습니다.

Layer-wise Propagation

위의 spectral graph convolution (식 $(4)$)을 기반으로 neural network를 구성할 수 있습니다. 우선, 식 $(4)$를 $K=1$로 설정하면, 다음과 같이 나타낼 수 있습니다.

\[g_{\theta'} \ast_G x \approx \theta'_0 x + \theta_1' (\tilde{L}x) \tag{5}\]

또한, 나아가 $\lambda_{\max} = 2$로 설정하면, $\tilde{L} = L - I$가 됩니다. 이를 이용하면, 식 $(5)$는 다음과 같이 나타낼 수 있습니다.

\[\begin{aligned} g_{\theta'} \ast_G x &\approx \theta_0' x + \theta_1'(L-I)x \\ &= \theta_0' x - \theta_1' D^{-\frac{1}{2}}AD^{-\frac{1}{2}}x \end{aligned} \tag{6}\]

이때 두 개의 parameter $\theta_0$과 $\theta_1$을 이용하여 노드의 특성을 업데이트할 수 있습니다. 또한, 이를 더 간단히 하여 $\theta = \theta_0’ = -\theta_1’$로 설정하면, 다음과 같이 나타낼 수 있습니다.

\[g_{\theta'} \ast_G x \approx \theta(I + D^{-\frac{1}{2}}AD^{-\frac{1}{2}})x \tag{7}\]

$\lambda_{\max} = 2$로 설정하였기 때문에 $I+D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$의 eigenvalue는 $[0, 2]$ 사이에 있습니다. 또한, 위 연산자 $(7)$을 반복적으로 사용할 경우 gradient vanishing/exploding 문제가 발생할 수 있습니다. 이를 해결하기 위해 Kipf와 Welling은 다음과 같은 renormalization trick을 제안하였습니다.

\[\begin{aligned} &I + D^{-\frac{1}{2}}AD^{-\frac{1}{2}} \rightarrow \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}} \\ &\tilde A = A + I\\ &\tilde D_{ii} = \sum_j \tilde A_{ij} \end{aligned}\]

이를 일반화하여, signal matrix $X\in \mathbb{R}^{N\times C}$에 대해 다음과 같이 노드의 특성을 업데이트할 수 있습니다 ($C$차원 feature vector). 이것이 바로 GCN의 layer-wise propagation 방식입니다. (식 $(1)$)

\[Z = \sigma(\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}XW) \tag{8}\]

$W\in \mathbb{R}^{C\times F}$는 가중치 행렬이며, 출력 행렬은 $Z\in \mathbb{R}^{N\times F}$입니다. 이러한 방식의 계산은 총 $O(\vert E\vert CF)$의 계산량을 가지며, 이를 이용하여 GCN을 구성할 수 있습니다.

PyTorch Implementation

Graph convolution layer를 PyTorch로 구현하면 다음과 같습니다.

import torch
import torch.nn as nn

class GraphConvolution(nn.Module):
    def __init__(self, in_features, out_features):
        super(GraphConvolution, self).__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.weight = nn.Parameter(torch.FloatTensor(in_features, out_features))
        self.reset_parameters()

    def forward(self, input, adj):
        support = torch.mm(input, self.weight)
        output = torch.spmm(adj, support)
        return output

    def reset_parameters(self):
        nn.init.xavier_uniform_(self.weight)

forward 메소드에서는 입력 input과 adjacency matrix adj를 이용하여 노드의 특성을 업데이트합니다. 이때 input은 노드의 특성을 나타내는 행렬이며, adj는 adjacency matrix입니다. reset_parameters 메소드에서는 가중치 행렬을 초기화합니다. 또한, torch.spmm은 sparse matrix와 dense matrix의 곱을 계산하는 함수입니다. 이를 이용하여 GCN을 구성할 수 있습니다.

import torch
import torch.nn as nn

class GCN(nn.Module):
    def __init__(self, in_features, hidden_features, out_features):
        super(GCN, self).__init__()
        self.gc1 = GraphConvolution(in_features, hidden_features)
        self.gc2 = GraphConvolution(hidden_features, out_features)

    def forward(self, x, adj):
        x = F.relu(self.gc1(x, adj))
        x = self.gc2(x, adj)
        return x

Spatio-Temporal Graph Convolutional Networks (STGCN)

이제 STGCN에 대해 알아보도록 하겠습니다. STGCN은 B. Yu, H. Yin, and Z. Zhu에 의해 2018년에 제안된 논문에서 처음 소개되었습니다. STGCN은 GCN을 시공간 데이터에 적용한 방법입니다. 이 논문에서는 교통량 예측에 STGCN을 적용하여 좋은 성능을 보였습니다.

STGCN Structure

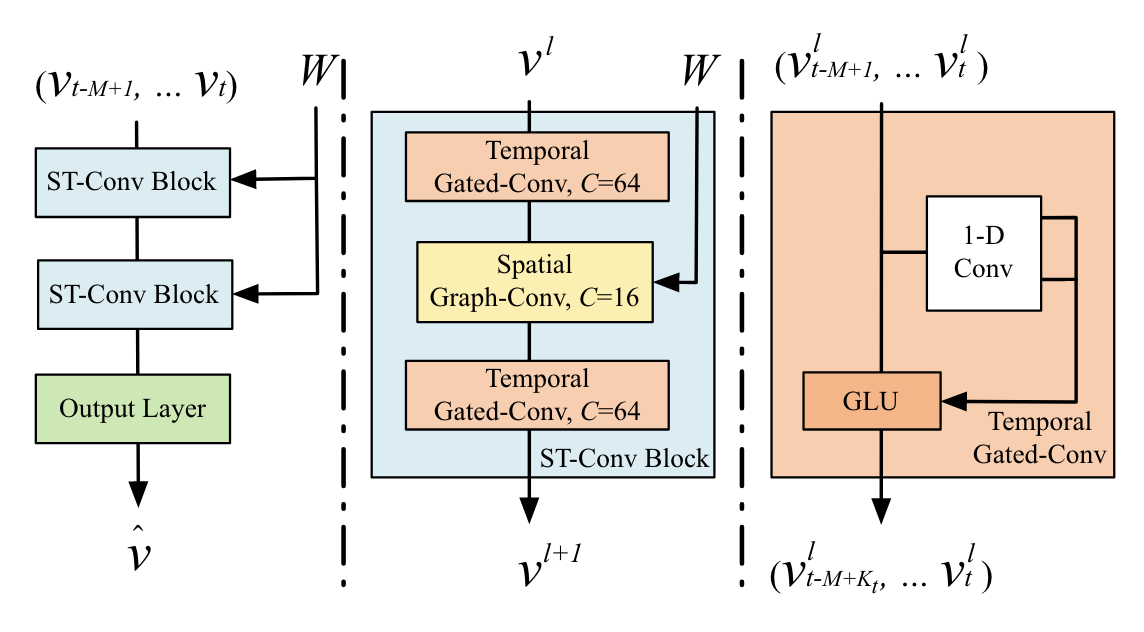STGCN Structure (Source: B. Yu, H. Yin, and Z. Zhu, 2018)

교통량 예측은 각 도로에 대해 일정 시간 간격으로 측정된 교통량 데이터를 이용하여 미래의 교통량을 예측하는 문제입니다. 이전 $M$ 시점의 교통량을 이용하여 $H$ 시점까지의 교통량을 예측하는 문제를 고려해보도록 하겠습니다. 전체 노드의 개수를 $n$ 이라고 하고 (여기서는 도로가 노드에 해당합니다) $v_t\in \mathbb{R}^{n}$ 을 시점 $t$ 의 각 노드의 교통량을 나타내는 벡터라고 하겠습니다. 그러면, 교통량 예측 문제는 다음과 같이 정의됩니다.

\[\begin{aligned} \hat{v}_{t+1},\ldots,\hat{v}_{t+H} &= \mathop{\arg\max}_{v_{t+1},\ldots,v_{t+H}} \log \Pr(v_{t+1},\ldots,v_{t+H} \vert v_{t-M+1},\ldots,v_t) \end{aligned}\tag{*}\]

공간적인 특성을 고려하는 것은 앞서 살펴본 GCN을 이용하여 풀 수 있습니다. 다만 시간적인 특성을 고려하는 것 역시 중요한데, 이를 해결하기 위해 STGCN에서는 Temporal Gated Convolution을 사용합니다.

Temporal Gated Convolution

위 그림의 오른쪽 부분을 살펴보면 Temporal Gated Convolution이라는 구조를 볼 수 있습니다. Temporal convolution layer는 다음과 같이 정의됩니다.

\[\begin{aligned} \Gamma \ast_{\cal T} Y &\triangleq P \odot \sigma(Q) \\ &\in \mathbb{R}^{(M-K_t + 1)\times C_o} \end{aligned} \tag{9}\]

식 $(9)$ 의 의미를 살펴보도록 하겠습니다. 우선, temporal convolution 연산은 너비가 $K_t$인 kernel을 이용한 1D convolution과 gated linear unit (GLU)를 이용합니다. 이때, 1D convolution 연산은 padding을 이용하지 않아, $M$개의 input은 $M-K_t+1$개의 output을 생성합니다.

즉, 각 노드에 대한 temporal convolution의 input이 $Y \in \mathbb{R}^{M\times C_i}$ 라면 convolution kernel은 $\Gamma \in \mathbb{R}^{K_t\times C_i\times C_o}$이며, output은

\[\begin{bmatrix}P & Q\end{bmatrix} \in \mathbb{R}^{(M-K_t+1)\times 2C_o}\]

입니다. 이때, $C_i$ 는 input feature의 차원, $C_o$ 는 output feature의 차원입니다. 또한, $P,Q$ 는 각각 $C_o$ 차원의 channel을 가집니다.

식 $(9)$에서 $\sigma$는 sigmoid 함수이며, $\odot$ 는 element-wise product^{Hadamard product}을 의미합니다. 따라서, Temporal Gated Convolution은 1D convolution으로 두 개의 output $P,Q$ 를 생성하고 이를 element-wise product하여 최종 output을 도출합니다.

Spatio-Temporal Convolution

이제, spatial convolution과 temporal convolution을 결합하여 Spatio-Temporal Convolution^ST-Conv을 정의할 수 있습니다. (위 그림의 2번째) 우선, 시공간성을 모두 고려해야 하므로 input, output은 모두 3D tensor로 정의됩니다.

$l$ 번째 ST-Conv block에 대한 Input tensor $v^l \in \mathbb{R}^{n\times M\times C^l}$ 는 $n$개의 노드, $M$ 개의 시점, $C^l$ 개의 feature로 이루어진 tensor입니다. 이때 output tensor는 다음과 같이 계산됩니다.

\[\begin{aligned} v^{l+1} &= \text{ST-Conv}(v^l) \\ &\triangleq \Gamma_1^l \ast_{\cal T} \text{ReLU}(g_\theta^l \ast_{G} (\Gamma_0^l \ast_{\cal T} v^l)) \\ &\in \mathbb{R}^{(M-2(K_t - 1))\times n\times C^{l+1}} \end{aligned}\]

2개의 temporal convolution layer와 1개의 graph convolution layer를 이용하여 ST-Conv을 구성합니다. 이러한 조합을 ST-Conv block이라고 부르며, STGCN은 2개의 ST-Conv block과 1개의 fully connected layer로 구성됩니다 (위 그림의 왼쪽).

Attention Based Spatial-Temporal Graph Convolutional Networks (ASTGCN)

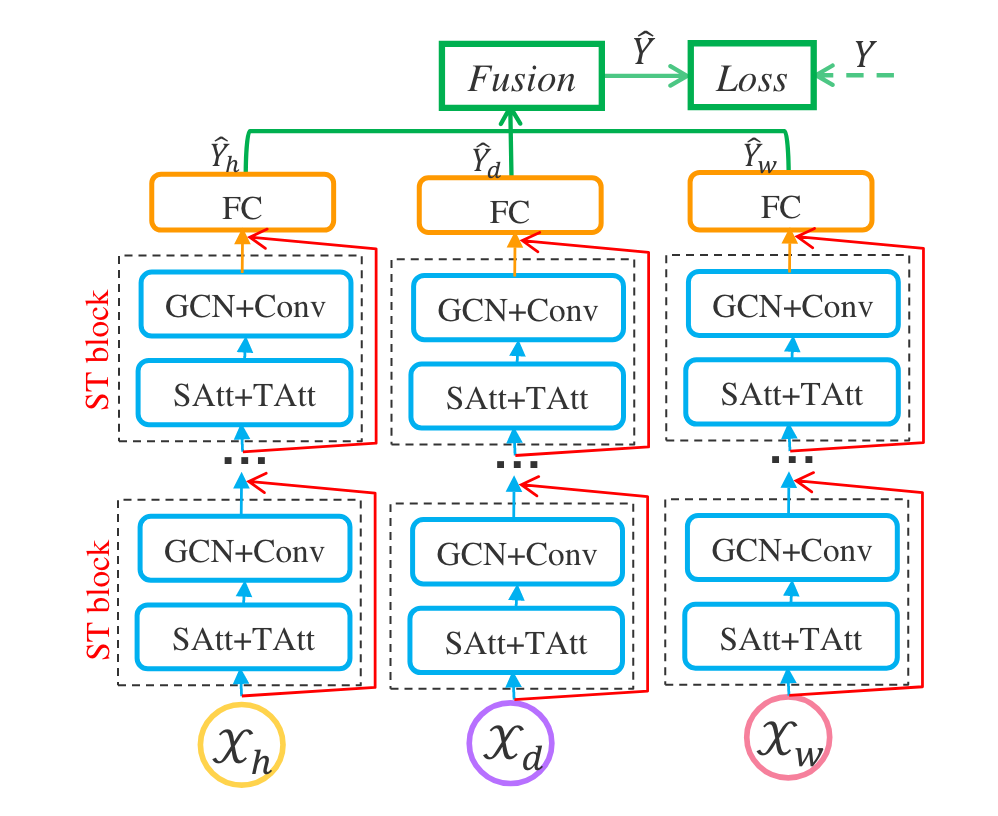ASTGCN Structure (Source: S. Guo, Y. Lin, N. Feng, C. Song, and H. Wan, 2019)

ASTGCN은 Attention Mechanism을 이용하여 STGCN을 개선한 방법입니다. 위 그림처럼 세 개의 동일한 네트워크를 학습하는데, 각각의 네트워크는 recent, daily-periodic, weekly-periodic pattern을 학습합니다. 이를 Fusion layer를 이용하여 결합하여 예측 결과를 도출합니다. 데이터가 수집된 주기를 $q$라고 하고, 예측할 시간 단위를 $H$라고 하겠습니다.

• Recent segment는 최근 $T_h$ 시간 단위의 데이터를 이용합니다. Input tensor는 $Y_h\in \mathbb{R}^{N \times F \times T_h}$이며, $N$은 노드의 개수, $F$는 feature의 개수, $T_h$는 시간 단위입니다. $Y_h$는 다음과 같이 주어집니다.

  \[Y_h = \begin{pmatrix} \mathbf{X}_{t-T_h+1}, \mathbf{X}_{t-T_h+2}, \ldots, \mathbf{X}_t \end{pmatrix}\]

• Daily-periodic segment는 일별 주기성을 학습합니다. Input tensor는 $Y_d\in \mathbb{R}^{N \times F \times T_d}$이며, $T_d$는 일 단위입니다. $Y_d$는 다음과 같이 주어집니다.

  \[Y_d = \begin{pmatrix} \mathbf{X}_{t-(T_d/H)*q+1}, \ldots, \mathbf{X}_{t-(T_d/H)*q+H}, \mathbf{X}_{t-(T_d/H-1)*q+1}, \ldots, \mathbf{X}_{t-(T_d/H-1)*q+H}, \ldots, \mathbf{X}_{t-q+1}, \ldots, \mathbf{X}_{t-q+H} \end{pmatrix}\]

  여기서 $q$는 샘플링이 이루어진 빈도를 의미하며, $H$는 예측할 시간 단위입니다 (식 $(*)$).

• Weekly-periodic segment는 주별 주기성을 학습합니다. Input tensor는 $Y_w\in \mathbb{R}^{N \times F \times T_w}$이며, $T_w$는 주 단위입니다. $Y_w$는 다음과 같이 주어집니다.

  \[Y_w = \begin{pmatrix} \mathbf{X}_{t-7(T_w/H)*q+1}, \ldots, \mathbf{X}_{t-7(T_w/H)*q+H}, \mathbf{X}_{t-7(T_w/H-1)*q+1}, \ldots, \mathbf{X}_{t-7(T_w/H-1)*q+H}, \ldots, \mathbf{X}_{t-7q+1}, \ldots, \mathbf{X}_{t-7q+H} \end{pmatrix}\]

  위와 같이, daily-periodic segment와 weekly-periodic segment는 각각 일별, 주별 주기성을 학습합니다. 또한, 위 정의에 따라 $T_h, T_d, T_w$ 는 모두 $q$의 배수가 되어야 합니다. 다음 그림을 참고하면, 각 segment의 구조를 쉽게 이해할 수 있습니다.

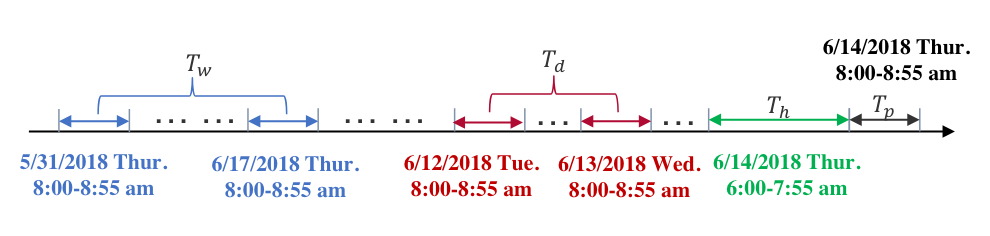Recent, Daily, Weekly segment (Source: S. Guo, Y. Lin, N. Feng, C. Song, and H. Wan, 2019)

Spatial-Temporal Attention Mechanism

ASTGCN에서 핵심이 되는 아이디어는 Spatial-Temporal Attention Mechanism입니다. 각 노드가 다른 노드에 미치는 영향을 고려하기 위해 Attention Mechanism을 이용합니다.

우선, Spatial attention은 다음과 같이 정의됩니다.

\[\begin{aligned} \mathbf{S} &= \mathbf{V}_s\cdot \sigma((Y_h^{(r-1)}\mathbf{W}_1)\mathbf{W}_2(\mathbf{W}_3Y_h^{(r-1)})^\top + \mathbf{b}_s) \\ \mathbf{S}_{ij}' &= \text{softmax}(\mathbf{S}_{ij}) \\ &= \frac{\exp(\mathbf{S}_{ij})}{\sum_{j=1}^N \exp(\mathbf{S}_{ij})} \end{aligned}\]

여기서 $Y_h^{(r-1)}\in\mathbb{R}^{N\times C_{r-1}\times T_{r-1}}$은 $r$번째 spatial-temporal block의 input tensor이며, $C_{r-1}$은 이전 block의 feature 차원을, $T_{r-1}$은 이전 block의 시간 길이를 의미합니다. $r=1$인 경우 $T_0$은 recent, daily-period, weekly-period component에서 각각 $T_h, T_d, T_w$를 의미합니다.

\(\mathbf{V}_s, \mathbf{W}_1, \mathbf{W}_2, \mathbf{W}_3, \mathbf{b}_s\) 는 학습 가능한 parameter입니다. $\sigma$는 활성화 함수로, 여기서는 sigmoid 함수를 사용합니다. $\mathbf{S}_{ij}’$는 spatial attention matrix로, 각 노드가 다른 노드에 미치는 영향을 나타냅니다.

이를 통해 계산한 $\mathbf{S}\in\mathbb{R}^{N\times N}$를 spatial attention matrix 라고 부르며, 이것에 softmax 함수를 적용하여 spatial attention matrix를 정규화합니다. $\mathbf{S}_{ij}’$는 노드 $i$와 노드 $j$의 correlation을 나타냅니다.

Temporal Attention Mechanism

다음으로, Temporal attention 역시 유사하게 정의할 수 있습니다.

\[\begin{aligned} \mathbf{E} &= \mathbf{V}_e\cdot \sigma(((Y_h^{(r-1)})^\top\mathbf{W}_4)\mathbf{W}_5(\mathbf{W}_6Y_h^{(r-1)}) + \mathbf{b}_e) \\ \mathbf{E}_{ij}' &= \text{softmax}(\mathbf{E}_{ij}) \\ &= \frac{\exp(\mathbf{E}_{ij})}{\sum_{j=1}^{T_{r-1}} \exp(\mathbf{E}_{ij})} \end{aligned}\]

Matrix $\mathbf{E}\in\mathbb{R}^{T_{r-1}\times T_{r-1}}$는 temporal attention matrix로, 이는 두 시점 간의 correlation을 나타냅니다.

Fusion Layer

마지막 단계에서는 세 개의 segment에서 얻은 정보를 결합하여 예측 결과를 도출합니다. 이를 위해 Fusion layer를 이용합니다. 이는 세 개의 learable weight matrix $\mathbf{W}_s, \mathbf{W}_d, \mathbf{W}_w$를 이용하여 다음과 같이 계산됩니다.

\[\hat{\mathbf{Y}} = \mathbf{W}_s \odot \mathbf{Y}_s + \mathbf{W}_d \odot \mathbf{Y}_d + \mathbf{W}_w \odot \mathbf{Y}_w\]

References

• B. Yu, H. Yin, and Z. Zhu, “Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting,” in Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, Jul. 2018, pp. 3634–3640. doi: 10.24963/ijcai.2018/505.
• S. Guo, Y. Lin, N. Feng, C. Song, and H. Wan, “Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting,” Proceedings of the AAAI Conference on Artificial Intelligence, vol. 33, no. 01, Art. no. 01, Jul. 2019, doi: 10.1609/aaai.v33i01.3301922.
• T. N. Kipf and M. Welling, “Semi-Supervised Classification with Graph Convolutional Networks.” arXiv, Feb. 22, 2017. doi: 10.48550/arXiv.1609.02907.