최근 공간 데이터에 대한 인과추론에 대해 관심을 가지고 여러 논문을 살펴보는 중인데, 기존 인과추론(Rubin의 인과 모델) 프레임워크는 SUTVAStable Unit Treatment Value Assumption 가정을 기반으로 하는데, 이 중 No interference라는 가정이 공간 데이터에서는 성립하지 않는 경우가 많습니다. 예를 들어, 특정 지역에 대한 처치가 인근 지역에 영향을 미치는 경우가 많기 때문입니다 (ex. 범죄학에서의 전이 효과 : 범죄예방 프로그램이 특정 지역에서 시행되면 인근 지역의 범죄율이 증가하는 경우). 이러한 문제를 spatial spillover effect 라고도 하는데, 최근에 이를 해결하기 위해 다양한 방법론들이 제안되고 있는 분야입니다. 이번 글과 향후 몇 개의 글을 통해 공간 데이터에서의 인과추론에 대한 최근 연구들을 정리해보려고 합니다.

Causal Inference with Spatio-Temporal Point Patterns

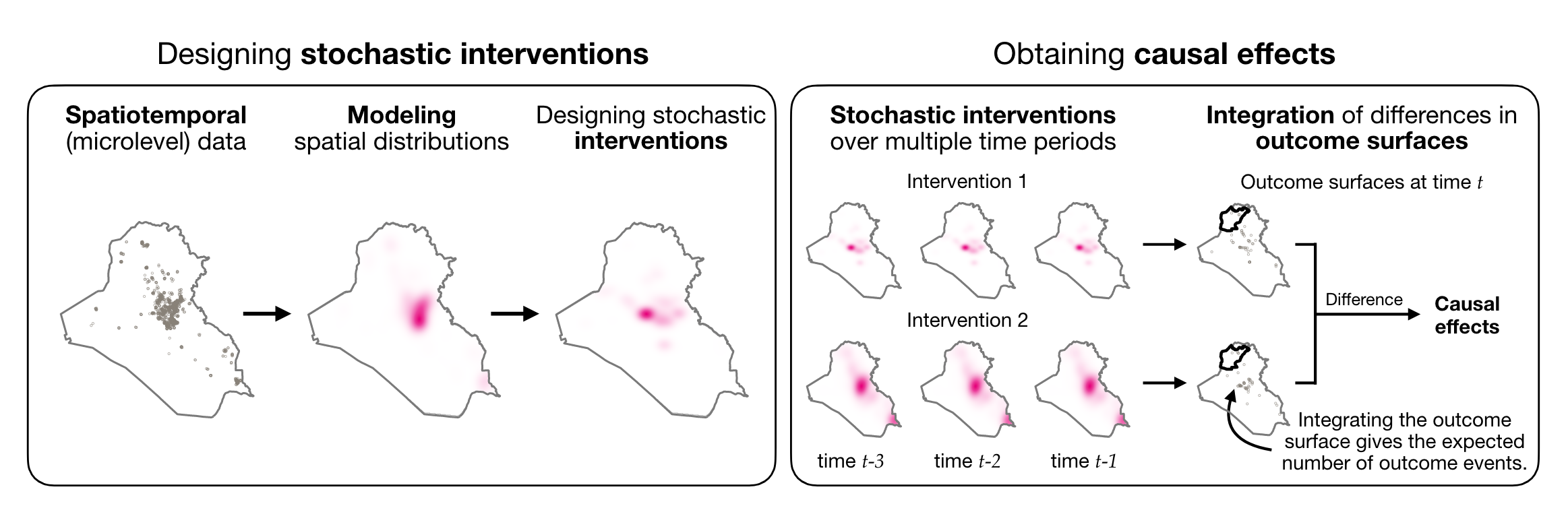프레임워크 요약 : M. Mukaigawara et al., 2025

이번 글에서는 Papadogeorgou et al., 2022 논문을 바탕으로 시공간 점 패턴(spatiotemporal point pattern)에서의 인과추론 방법론을 소개합니다. (시)공간 점 패턴은 특정 지역에 사건이 발생하는 패턴을 분석하는 방법으로, 예를 들어 범죄 사건, 질병 발생, 식물 분포 등을 분석할 때 사용됩니다. 이 논문에서는 공중 폭격(point)이 이라크 내 반란(point)에 미치는 영향을 분석하기 위해 공간 점 패턴을 활용한 인과추론 방법론을 제안합니다.

\[\text{Airstrike} \rightarrow \text{Insurgent violence}\]

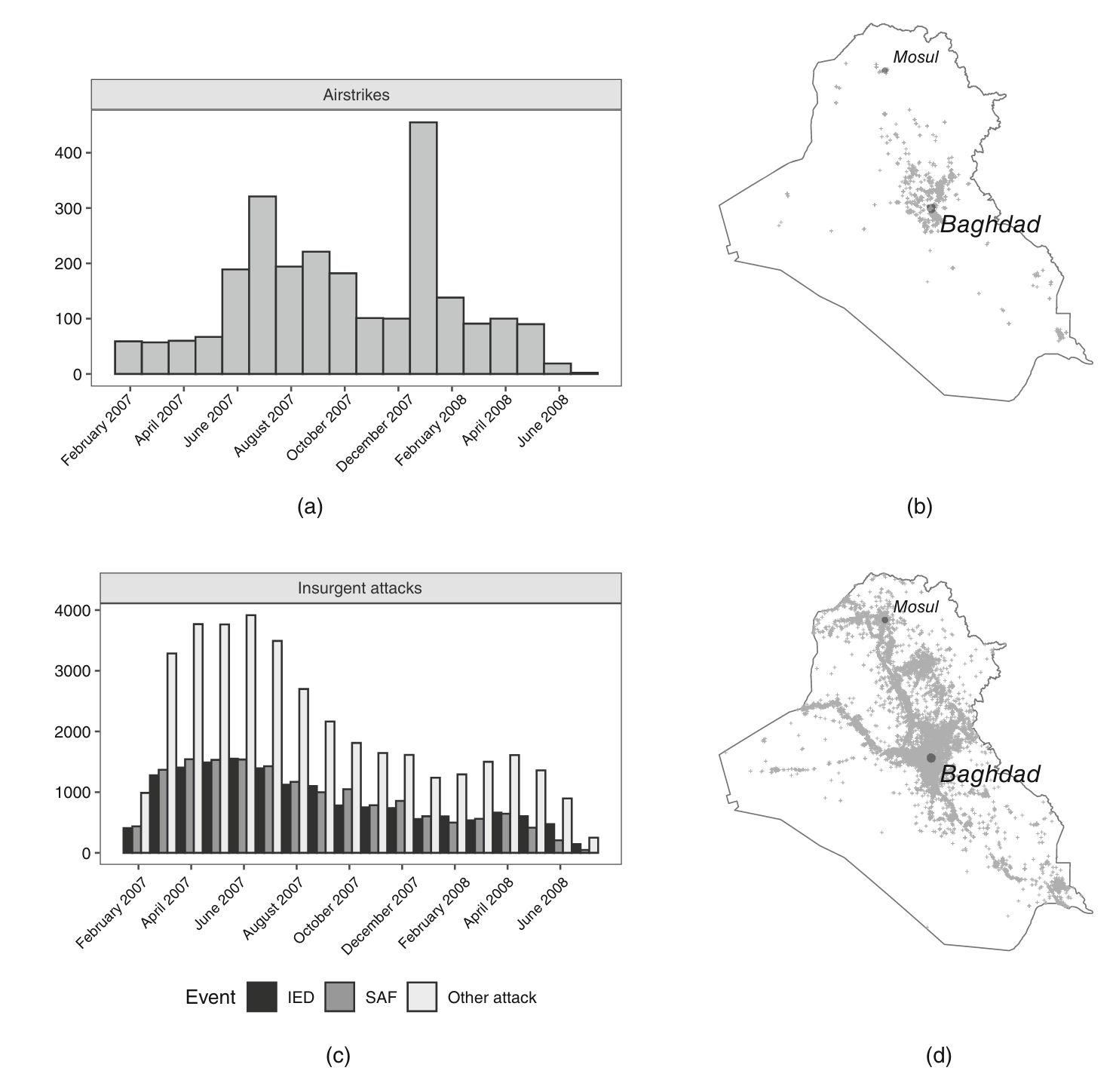공중 폭격 지점(위)과 반란 지점(아래)의 시각화

Setup

이 논문에서는 다음과 같은 설정을 가정합니다. 공간 점 패턴에 대한 자세한 내용은 여기를 참고하시기 바랍니다.

  • $\Omega$ : 공간 영역 (ex. 이라크의 특정 지역)
  • $W_{t}(s), s\in\Omega$ : 시점 $t$에서의 처치변수 (점 패턴)
  • $\mathcal{W}$ : set of all possible point patterns (i.e. $\forall t, W_{t}\in\mathcal{W}$)
  • $S_{W_{t}} = {s\in\Omega\vert W_{t}(s)=1}$ : Treatment-active locations
  • \(\overline{\mathbf{W}_{t}}=(W_{1},\ldots,W_{t})\) : collection of treatments
  • \(w_{t}\) : realisation of \(W_{t}(s)\) (관측된 점 패턴)
  • \(\bar w_{t}=(w_{1},\ldots,w_{t})\) : history of point pattern at $T=t$
  • $Y_{t}(\bar w_{t})$ : potential outcome at $t\in\mathcal{T}$, with given treatment sequence(history) $\bar w_{t}\in\mathcal{W}^{t}$
  • \(S_{Y_{t}(\bar w_{t})}=S_{Y_{t}}\) : Outcome-active locations
  • \(\bar{\mathcal{Y}}_{T}= \{Y_{t}(\bar w_{t})\vert \bar w_{t}\in\mathcal{W}^{t}, t\in \mathcal{T}\}\) : set of all possible potential outcomes
  • \(\overline{\mathbf{Y}_{t}}=\{Y_{1},\ldots,Y_{t}\}\) : collection of observed outcomes
  • \(\mathbf{X}_{t}\): set of time-varying confounders that are realised prior to \(W_{t}\) but after \(W_{t-1}\)
  • \(\bar{\mathcal{X}}_{T} = \{X_{t}(\bar w_{t-1}\vert\bar w_{t-1}\in\mathcal{W}^{t-1},t\in\mathcal{T}\}\) : set of all possible covariates
  • \(\bar H_{t} = \{\mathbf{W_{t},Y_{t},X_{t+1}}\}\) : observed history preceding \(W_{t+1}\)

모든 표기를 기억할 필요는 없습니다만, 처치 변수인 $W_{t}$가 공간 $\Omega$에 존재하는 점 패턴으로 주어지는 것과 $Y_t$가 시점 $t$에서 처치변수 $W_{t}$에 따라 달라지는 잠재적 결과변수라는 점을 기억하시면 좋습니다.

Causal Estimand

일반적으로 인과추론에서는 처치효과를 어떤 추정치로 측정할 것인지에 대한 문제가 중요하며, 주로 ATEAverage Treatment Effect를 사용합니다. ATE는 처치가 주어졌을 때와 주어지지 않았을 때의 결과의 차이를 의미합니다. 즉, 처치가 주어졌을 때와 주어지지 않았을 때의 평균 결과의 차이를 나타내며, 이는 인과관계를 추론하는 데 중요한 역할을 합니다.

이 논문에서는 처치효과가 점 과정으로 주어지기 때문에, 이에 맞는 ATEAverage Treatment Effect를 정의합니다.

Stochastic Intervention

일반적으로 인과추론에서는 처치변수 $W_{t}$가 고정된 값으로 주어지지만, 이 논문에서는 처치변수의 확률분포를 이용하며, 구체적으로는 intensity function강도함수 $h:\Omega\to[0,\infty)$를 갖는 포아송 점 과정(Poisson Point Process)를 가정합니다.

$F_h$를 강도함수 $h$에 대한 공간 점 과정의 분포라고 하고, $N_B$를 영역 $B\subset\Omega$에 대한 카운팅 측도라고 하겠습니다 ($B$에서의 사건 발생 횟수). 이때, 시점 $t$에서와 공간 $B$에서의 결과-활성 지역(outcome-active locations)의 기대값은 다음과 같이 정의됩니다.

\[\begin{align} N_{Bt}(F_{h}) &= \int_{\mathcal{W}}N_{B}(Y_{t}(\bar W_{t-1},w_{t}))dF_{h}(w_{t})\\ &= \int_{\mathcal{W}}\bigg\vert S_{Y_{t}(\bar W_{t-1},w_{t})}\cap B\bigg\vert dF_{h}(w_{t}) \end{align}\]

여기서 결과-활성 지역이란, 특정 시점과 영역에 대해 처치가 발생했을 때, 결과가 발생하는 지점을 의미합니다. 예를 들면, 처치변수인 공중 폭격 지점이 분포 $F_h$에 따라 주어졌을 때, 위 기댓값은 지역 $B$, 시점 $t$에서 반란이 몇 곳에서 발생할지에 대한 기대값을 의미합니다.

이때, 위 식은 한번의 처치에 대해 계산이 이뤄지는 것이므로 연속된 $M$번에 대한 처치에 대해서는 다음과 같이 확장할 수 있습니다.

\[\begin{align} N_{Bt}(F_{h}) &= \int_{\mathcal{W}}N_{B}(Y_{t}(\bar W_{t-1},w_{t-M+1},\ldots,w_{t}))dF_{h_{1}}(w_{t})\cdots dF_{h_{M}}(w_{t-M+1})\\ &= \int_{\mathcal{W}}\bigg\vert S_{Y_{t}(\bar W_{t-1},w_{t-M+1},\ldots,w_{t})}\cap B\bigg\vert dF_{h_{1}}(w_{t})\cdots dF_{h_{M}}(w_{t-M+1}) \end{align}\]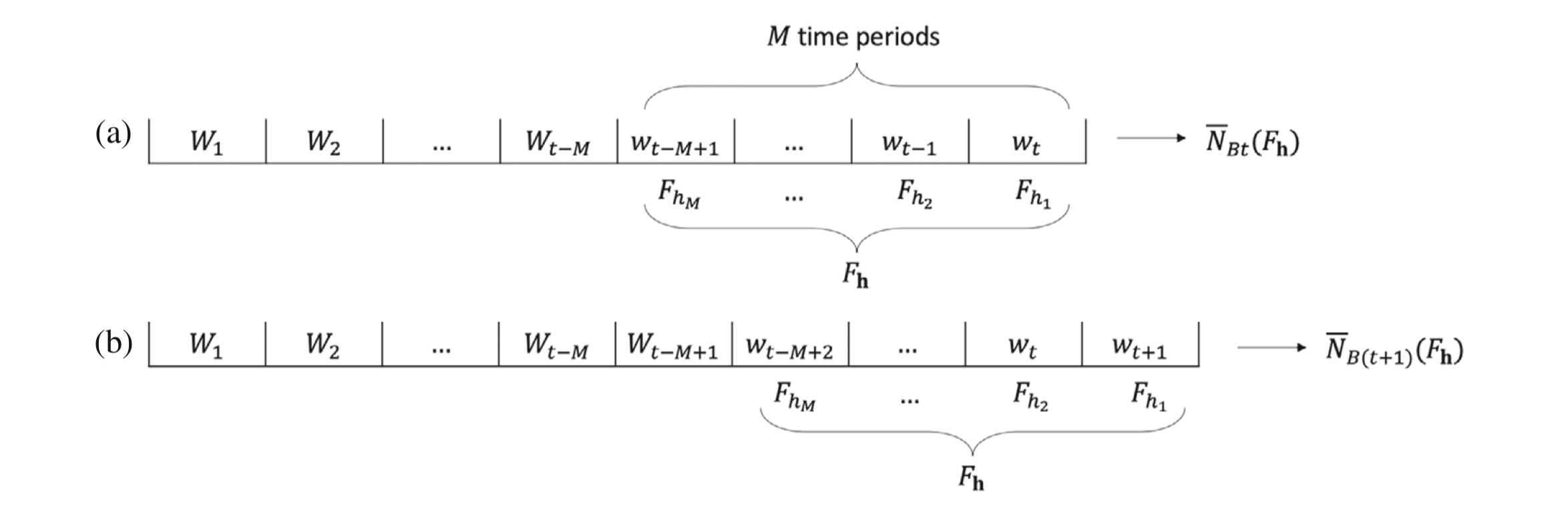

위 측정값은 시점 $t$와 지역 $B$에서, 이전 $M$개 시점에서의 처치효과가 분포 $F_\mathbf{h}=F_{h_{1}}\times \cdots \times F_{h_{M}}$ 를 따를 때 결과 발생 횟수의 기댓값을 나타냅니다. 물론, 각 시점에서의 처치효과가 동일한 분포를 따른다고 가정하여 $F_\mathbf{h}= F_{h}^{M}$ 이 됨을 상정할 수도 있습니다.

Average treatment effect(ATE)

위 세팅을 이용하여, 확률적 처치 $F_\mathbf{h’}$ vs $F_\mathbf{h’’}$에 대한 ATE는 다음과 같이 정의됩니다.

\[\tau_{Bt}(F_\mathbf{h'},F_\mathbf{h''}) = N_{Bt}(F_\mathbf{h''}) -N_{Bt}(F_\mathbf{h'})\]

이는 시점 $t$, 지역 $B$에서의 처치효과가 $F_\mathbf{h’’}$일 때와 $F_\mathbf{h’}$일 때의 결과 발생 횟수의 기댓값 차이를 의미하며,

이를 여러 시점($M$시점부터 $T$시점까지)에 대해 평균을 내면, 전체 시점에서의 평균 ATE를 구할 수 있습니다 (아래).

\[\tau_{B}(F_\mathbf{h'},F_\mathbf{h''}) = \frac{1}{T-M+1}\sum_{t=M}^{T}\tau_{Bt}(F_\mathbf{h'},F_\mathbf{h''})\]

Estimation of ATE

앞서 정의한 추정치를 구하기 위해서 이 논문에서는 성향점수propensity score $e_{j}(w)$ 기반 IPWInverse Probability Weighting 추정을 제안합니다. 성향점수는 주어진 관측치가 처치받을 확률을 나타내는 값으로, 위 세팅에서는 다음과 같이 정의됩니다.

\[e_{t}(w)= f(W_{t}| \overline{\mathbf{W}}_{t-1},\overline{\mathcal{Y}}_{T}, \overline{\mathcal{X}}_{T})= f(W_{t}=w\vert\bar H_{t-1})\]

다음으로는, 커널 평활법kernel smoothing을 이용하기 위해 단변량 커널함수 $K:[0,\infty)\to[0,\infty), \int K(u)du=1$를 정의하고, 커널 $K$에 대해 스케일된 버전 $K_{b}(u):= b^{-1}K(\frac{u}{b})$를 정의합니다 ($b$는 대역폭).

추정은 두 단계로 진행됩니다.

  1. 각 시점 $t$에서, 결과-활성 지역(outcome-active locations)을 커널에 따라 평활화합니다.
  2. 평활화된 결과 활성 지역이 관측된 처치 패턴의 상대 밀도(처치에서의 분포 vs. 실제 데이터 생성 과정)로 가중됩니다(weighted).

이때, 다음과 같은 추정치 $\hat Y_{t}(F_{h}^{M};\omega):\Omega\to\mathbb{R}^+$를 정의합니다.

\[\hat Y_{t}(F_{h}^{M};\omega)=\prod_{j=t-M+1}^{t} \frac{f_{h}(W_{j})}{e_{j}(W_{j})}\bigg[\sum_{s\in S_{Y_{t}}} K_{b}(\Vert \omega-s\Vert )\bigg]\]

위 식에서 상대밀도 $f_{h}/e_{j}$가 위 2단계의 가중치에 대응됩니다.

커널 $K$가 연속형이면 $\hat Y_{t}(F_{h}^{M};\omega)$는 $\Omega$에 대해 연속적인 함수가 되므로, 이는 강도함수로 해석될 수 있습니다. 따라서

\[\hat N_{Bt}(F_{h}^{M}) = \int_{B}\hat Y_{t}(F_{h}^{M};\omega)d\omega\]

와 같이 $B, t$에서의 카운팅 측도를 추정할 수 있습니다. 마찬가지로, 이를 $M$개의 시점에 대해 평균을 내면

\[\hat N_{B}(F_{h}^{M})= \frac{1}{T-M+1}\sum_{t=M}^{T}\hat N_{Bt}(F_{h}^{M})\tag{2}\]

를 얻을 수 있으므로, 결과적으로 ATE 추정치는 다음과 같이 구할 수 있습니다.

\[\hat \tau_{B}(F_{h_{1}}^{M} , F_{h_{2}}^{M})= \hat N_{B}(F_{h_{2}})-\hat N_{B}(F_{h_{1}}^{M})\]

Hajek estimator

인과추론에서 성향점수 기반의 IPW 추정량을 사용하여 ATE를 추정하는 방법은 잘 알려져 있습니다. 또한, IPW 추정량을 보완하기 위해 Horvitz-Thompson estimator와 Hajek estimator를 사용하는 방법도 있습니다 (참고). 이 논문에서도 Hajek estimator를 사용하여 IPW 가중치를 표준화하고, 위 (2)을 다음과 같이 대체합니다.

\[\hat{N}_{B}(F_{h}^{M}) = \frac{\sum_{t=M}^{T}\hat{N}_{Bt}(F_{h}^{M})}{\sum_{t=M}^{T}\{\prod_{j=t-M+1}^{t} \frac{f_{h}(W_{j})}{e_{j}(W_{j})}\}}\]

논문의 시뮬레이션 결과에 따르면, Hajek estimator를 사용한 경우가 IPW 추정량보다 더 좋은 성능을 보였습니다.

Propensity score model

실제 데이터를 이용해 인과추론을 진행하기 위해서는, 앞서 정의된 성향점수 $e_{t}(w)$를 추정해야 합니다. 이 논문에서는 강도함수 $\lambda_t$를 갖는 non-homogeneous Poisson point process

\[\lambda_t(s) = \exp(\beta_{0}+\mathbf{X}_t(s)^T\boldsymbol{\beta})\]

를 사용하여 성향점수를 추정합니다. 여기서 $\mathbf{X}_t(s)$는 시점 $t$에서의 공변량(covariates)입니다.

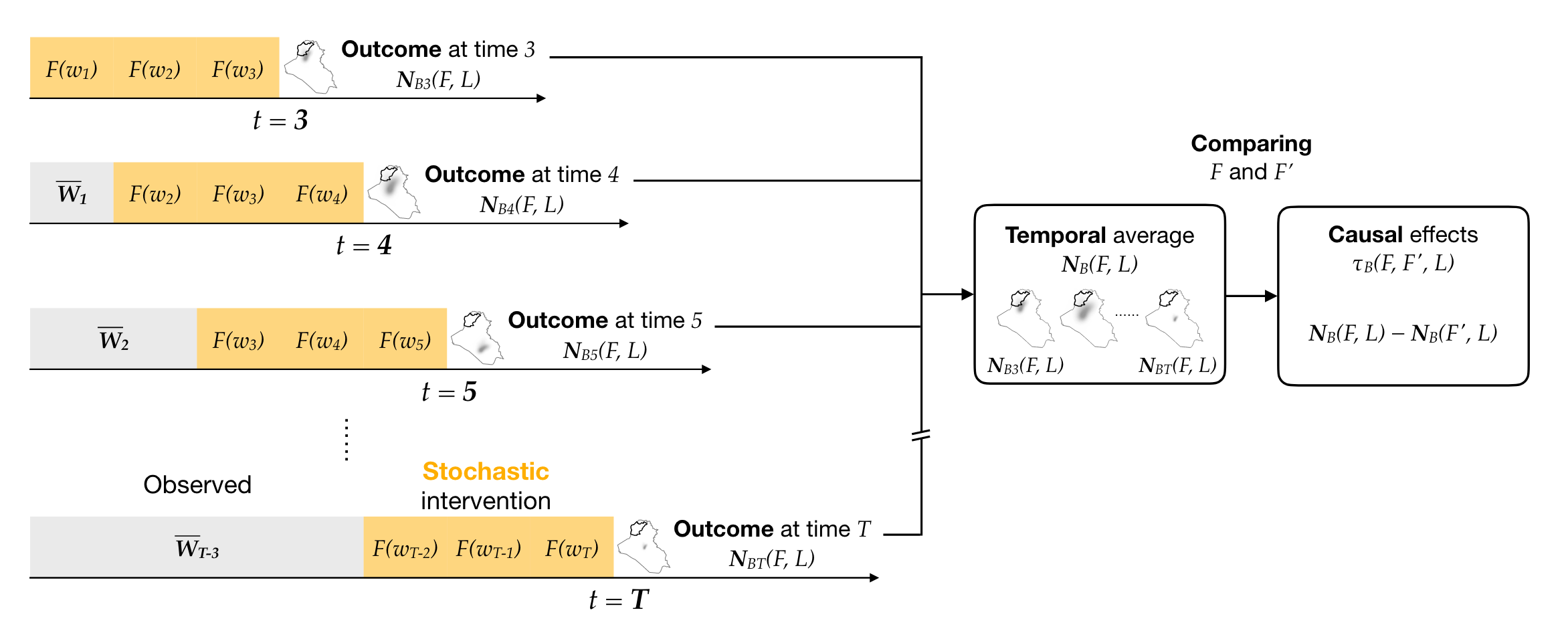논문에서 제안한 방법론 요약 : M. Mukaigawara et al., 2025

References

  • G. Papadogeorgou, K. Imai, J. Lyall, and F. Li, “Causal Inference with Spatio-Temporal Data: Estimating the Effects of Airstrikes on Insurgent Violence in Iraq,” Journal of the Royal Statistical Society Series B: Statistical Methodology, vol. 84, no. 5, pp. 1969–1999, Nov. 2022, doi: 10.1111/rssb.12548.
  • M. Mukaigawara, K. Imai, J. Lyall, and G. Papadogeorgou, “Spatiotemporal causal inference with arbitrary spillover and carryover effects,” Apr. 04, 2025, arXiv: arXiv:2504.03464. doi: 10.48550/arXiv.2504.03464.

Leave a comment