공간 데이터에서의 인과추론 : (2) Point vs. Area
이전 글에서는 처치변수와 결과변수가 모두 점 패턴인 경우에 대한 인과추론 방법론을 소개했습니다. 이번 글에서는 처치변수는 점 패턴으로 주어지지만 결과변수가 격자형으로 주어지는 areal data에 대한 인과추론 방법론을 소개합니다. 사실 많은 사회적 변수들이 areal data로 수집되는 경우가 많기 때문에 (ex. 행정구역별 통계, 격자별 인구 등) 이 논문에서 제안하는 방법론은 매우 유용할 것으로 보입니다. 이번 글은 2022년 JASA에 게재된 논문 Christiansen et al., 2022 를 바탕으로 작성하였습니다.
Casual Inference with Spatio-Temporal Point Patterns and Areal Data
이 논문에서는 conflict, 즉 내전과 같은 폭력적 사건이 콜롬비아의 산림 파괴에 미치는 영향을 분석하기 위해 공간 점 패턴을 활용한 인과추론 방법론을 제안합니다. 내전과 같은 사건은 특정 좌표를 갖는 점 과정으로 모델링할 수 있으며, 산림 파괴 정도는 실제 나무들의 파괴 정도를 모두 측정하기 어렵기 때문에 위성 사진을 바탕으로 격자형으로 모델링할 수 있습니다. 또한, 공변량으로는 인근 도로까지의 거리(km)를 사용합니다. 아래 그림은 이 논문에서 사용한 데이터셋을 시각화한 것입니다.
- $X^{t}_{s}$ : 처치변수 (conflict)로서 시점 $t$에서의 격자 $s$에 대한 값
- $Y^{t}_{s}$ : 결과변수 (forest loss)로서 시점 $t$에서의 격자 $s$에 대한 값
- $W^{t}_{s}$ : 공변량 (distance to road)로서 시점 $t$에서의 격자 $s$에 대한 값
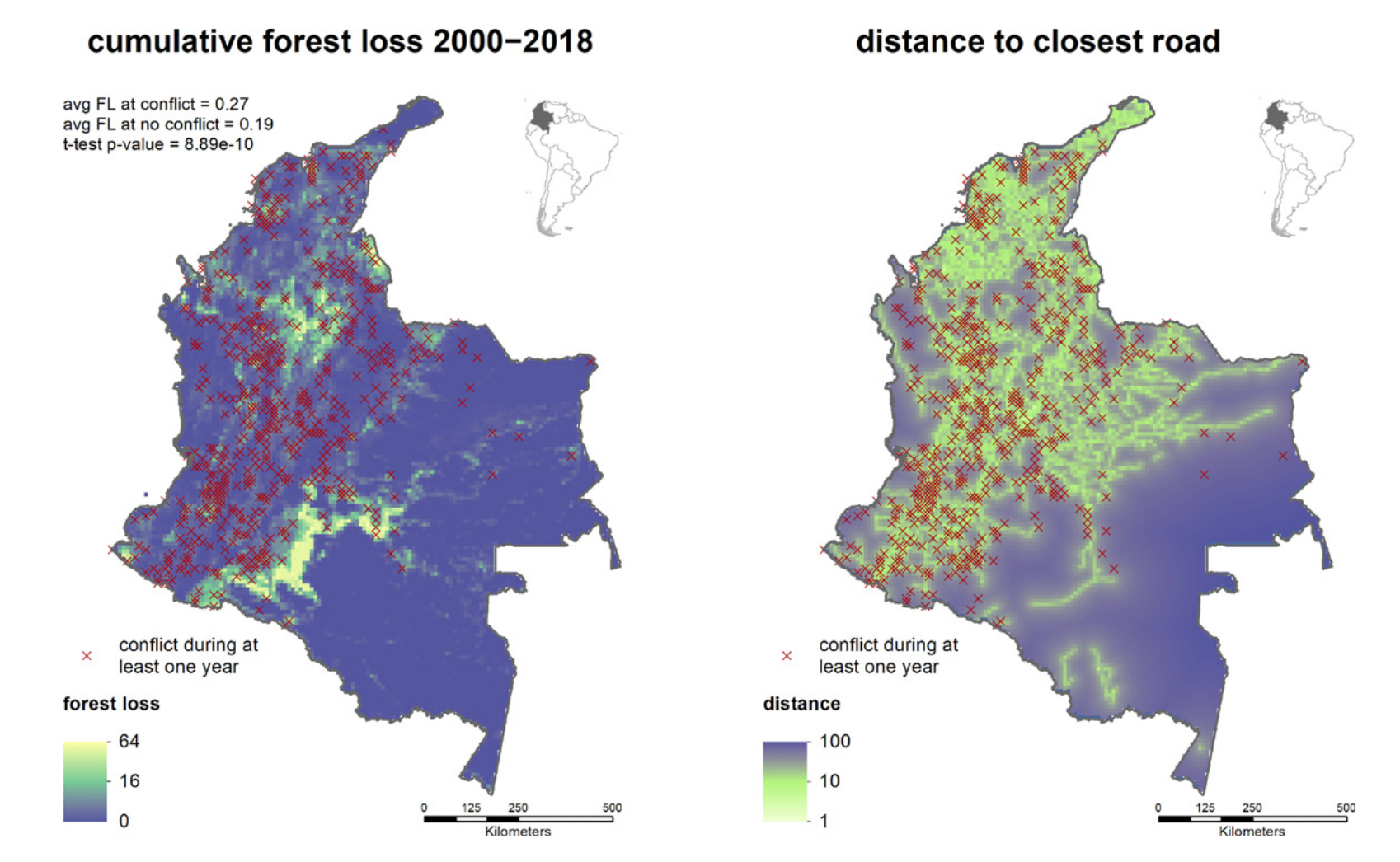 왼쪽 : 처치변수(Conflict, 빨간색 마커) vs. 결과변수(Forest loss, 격자형), 오른쪽 : 공변량(도로까지의 거리)
왼쪽 : 처치변수(Conflict, 빨간색 마커) vs. 결과변수(Forest loss, 격자형), 오른쪽 : 공변량(도로까지의 거리)
Setup
이 논문에서는 이전 글과 마찬가지로, (시)공간 점 과정spatiotemporal point process $\mathbf{Z}$을 사용하여 처치변수를 모델링합니다. 이때, 시공간 점 과정에 대해 다음과 같은 표기를 사용합니다.
- $\mathbf{Z}_{s}$ : 위치 $s$에서의 시간 과정(temporal process)
- $\mathbf{Z}^{t}$ : 시간 $t$에서의 공간 과정(spatial process)
- $\mathbf{Z}^{(S)}$ : 변수 $S\subseteq{1,\ldots,p}$에 대해 정의되는 시공간 과정(spatiotemporal process)
또한, 논문에서는 인과관계를 모델링하기 위해 다음과 같이 DAGDirected Acyclic Graph을 정의합니다 (참고 : DAG).
Causal Graphical Model for Spatio-Temporal Process
시공간과정 $\mathbf{Z}$에 causal graphical model은 다음과 같이 세 개의 요소로 정의됩니다.
-
Family \(\mathcal{S}=(S_j)_{j=1}^k\) : 비어있지 않고 서로소인 집합 \(S_1,\ldots,S_k\subset\{1,\ldots,p\}\)의 모임으로, \(\bigcup_{j=1}^k S_j = \{1,\ldots,p\}\)를 만족합니다.
-
Directed Acyclic Graph \(G\) : 정점 \(S_1,\ldots,S_k\)를 갖는 방향 비순환 그래프(DAG)
-
Family \(\mathcal{P}=(\mathcal{P}^j)_{j=1}^k\) : 각 $j$에 대해 분포 \(\mathcal{P}^{j}=\{\mathcal{P}^{j}_{z}\}_{z\in\mathcal{Z}_{|PA_{j}|}}\) 의 모임으로, $PA_{j}$는 노드 $S_j$의 부모 노드(parent node)들의 모임입니다. 만약 \(PA_j=\emptyset\)인 경우, $\mathcal{P}_j$는 단일 분포로 구성되며 이를 $P_j$라고 합니다.
정의는 복잡하지만, 간단히 말하면 좌표 $S_1,\ldots, S_k$에서 정의되는 시공간 과정의 분포를 DAG로 표현하고자 하는 것입니다. 또한, DAG는 각 노드에 순서를 차례대로 부여할 수 있는 성질을 갖기 때문에, 다음과 같이 joint distribution을 정의할 수 있습니다.
\[\begin{aligned} P(F) &:= P \circ \mathbf{Z}^{-1}(F) \\ &= \int_{F_1} \cdots \int_{F_k} P_{z^{PA_k}}^k(dz^{(S_k)}) \cdots P^1(dz^{(S_1)}) \end{aligned}\]이때 전체 확률측도 $P$를 observational distribution관측 분포라고 정의하며, DAG의 성질에 의해 $\mathbf{Z^{(PA_j)}}$가 주어진 경우 $\mathbf{Z^{(S_j)}}$의 조건부 분포는 $P_j$로 주어집니다. 또한, 처치(intervention)란 특정 노드 $S_j$에 대해 분포 $P_j$를 다른 분포 $\tilde{P}_j$로 대체하는 것을 의미합니다. 이때 변화된 전체 확률측도를 $\tilde{P}$라고 정의하며, 이를 interventional distribution처치 분포라고 합니다.
또한, DAG로 주어지는 시공간과정 $\mathbf{Z}$를 다음과 같이 표현합니다.
\[\mathbf{Z} = \left[\mathbf{Z}^{(S_k)} | \mathbf{Z}^{(PA_k)}\right] \cdots \left[\mathbf{Z}^{(S_1)}\right]\]Latent Spatial Causal Model
앞서 그래프 모델을 정의하는 데 상당히 복잡한 수식이 등장했지만, 결국 인과관계를 모델링하기 위한 방법론이기 때문에 우리는 처치변수 $X$, 결과변수 $Y$, 잠재변수 $H$에 대해서만 DAG를 정의하면 됩니다. 이를 Latent Spatial Causal Model(LSCM)이라고 하며, 다음과 같이 정의합니다.
\[(\mathbf{X},\mathbf{Y},\mathbf{H}) = \left[\mathbf{Y} | \mathbf{X},\mathbf{H}\right] \left[\mathbf{X} | \mathbf{H}\right] [\mathbf{H}]\]여기서 다음 두 가정을 만족해야 합니다.
- Latent process $\mathbf{H}$는 time-invariant하며, weakly stationary 합니다. 즉, $\mathbf{H}$는 시공간과정이지만, 시간에 따라 변하지 않는다는 것입니다.
- 함수 $f$와 i.i.d.인 공간 오차변수 $\epsilon^1,\ldots$이 존재하여 $(\mathbf{X},\mathbf{H})$와 독립이고, 다음 과 같은 관계를 만족합니다.
Causal Estimand
위 LSCM을 바탕으로, 처치 효과는 다음과 같이 정의되며 이를 Average causal effect라고 합니다.
\[f_{\text{AVE}(X\to Y)}(x) := \mathbb{E}[f(x, H_0^1, \epsilon_0^1)]\]이때, 위 인과효과는 노이즈 변수 $\epsilon$와 숨겨진 변수 $H$에 대한 기대값을 취한 평균 효과입니다. 하지만 처치 분포 $P_x$를 직접적으로 알 수 없기 때문에, Fubini의 정리를 이용하여 다음과 같은 관계를 유도하고 이를 구할 수 있습니다.
\[f_{\text{AVE}(X\to Y)}(x) = \mathbb{E}[f_{Y|(X,H)}(x, H_{0^1)]}\tag{*}\]여기서 함수 \(f_{Y|(X,H)}\) 는 처치변수 $X$와 공변량 $H$에 대한 조건부 기대값을 의미하므로, 이는 회귀모형
\[(x,h) \mapsto \mathbb{E}[Y_s^t|(X_s^t=x,H_s^t=h)]\]로 해석할 수 있습니다. 따라서, 실제 데이터로부터 인과효과를 추정하기 위해서는 (잠재 변수를 알 수 없다고 가정하면) 데이터 $(\mathbf{X},\mathbf{Y})$를 위 기댓값을 추정해야 할 것입니다.
Estimation
이제 실제 데이터로부터 앞서 정의한 인과효과를 추정하기 위해 어떻게 접근해야 할지 알아보겠습니다. 우선, 시공간 데이터가 $n$개의 공간 격자 $s_1,\ldots,s_n$에 대해 $m$개의 시점 $1,\ldots,m$에서 관측되었다고 가정하겠습니다. 즉, $(s,t) \in {s_1,\ldots,s_n} \times {1,\ldots,m}$에 대해 $(X_s^t,Y_s^t)$가 관측되었다고 가정합니다.
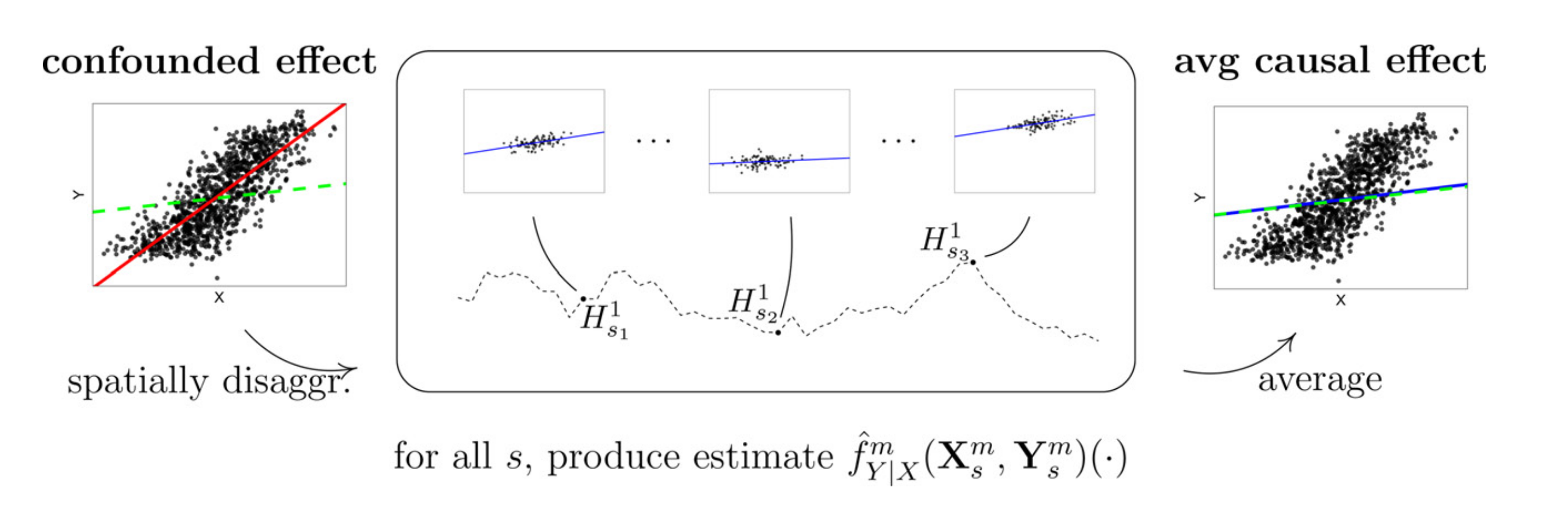 추정 과정의 전반적인 아이디어
추정 과정의 전반적인 아이디어
이때, 추정 과정의 전반적인 아이디어는 다음과 같습니다.
-
모든 \(s\in\{s_{1},\ldots,s_{n}\}\) 에 대해 조건부 분포 \(Y_{s}^{t}|(X_{s}^{t},H_{s}^{t})\) 를 가정한 데이터 \((X_{s}^{t},Y_{s}^{t})\) 들이 관측됨
-
$\mathbf{H}$가 시간에 따라 불변이므로 \(f_{Y|(X,H)}(\cdot,h_{s})\) 는 $m$개의 데이터 \(\{(X_{s}^{t},Y_{s}^{t})\}_{t=1}^{m}\) 으로부터 추정될 수 있음
-
앞선 기댓값 $(*)$는 $n$개의 지점 $s_{i}$들의 평균을 통해 근사할 수 있음:
이 과정에서 회귀모형 $f$를 어떤 모델로 선택할 것인지(ex. GBM, Random Forest, Linear Regression 등)는 분석 과정 이전에 임의로 설정해야 할 것입니다. 위 추정 과정의 아이디어는 위 그림을 통해 살펴보면 보다 쉽게 이해할 수 있습니다.
또한, 위 추정량은 consistency를 만족하는데, 이와 관련된 내용은 논문을 참고하시기 바랍니다.
Testing
논문에서는 인과효과를 추정하는 것 외에도 처치효과가 존재하는지에 대한 검정도 제안합니다. 이때, 검정의 귀무가설은 다음과 같이 정의됩니다.
$H_0$ : $(X, Y)$는 $f$가 $X^t_s$에 대해 상수인 LSCM으로부터 비롯되었다.
여기서 $f$가 $X^t_s$에 대해 상수라는 것은 처치변수 $X^t_s$가 결과변수 $Y^t_s$에 영향을 미치지 않는다는 것을 의미하므로, 귀무가설은 처치효과가 존재하지 않는다는 것입니다.
검정은 resampling test를 통해 수행되며, 임의의 검정통계량 $T$를 정의하고, 데이터셋의 permutation을 $\sigma(\mathbf{X},\mathbf{Y})$라고 하겠습니다. 반복횟수 $B$에 대해 다음과 같이 확률 $p_{\hat T}$를 정의합니다.
\[p_{\hat T}(\mathbf{x},\mathbf{y}) = \frac{1+|\{b\in \{1,\ldots,B\}:\hat T(\sigma_{k_b}(\mathbf{x},\mathbf{y})) \ge \hat T(\mathbf{x},\mathbf{y})\}|}{1+B}\]그러면 검정 $\varphi_{\hat T}^\alpha=1 \Leftrightarrow p_{\hat T}\le \alpha$는 level $\alpha$의 검정이 됩니다. 논문에서는 검정통계량으로 어떤 함수 $\psi$에 대해 다음과 같은 plug-in estimator를 제안합니다.
\[\hat T(\mathbf{X}_n^m,\mathbf{Y}_n^m) = \psi(\hat f_{\text{AVE}(X\to Y)}^{nm}(\mathbf{X}_n^m,\mathbf{Y}_n^m))\]Experiment
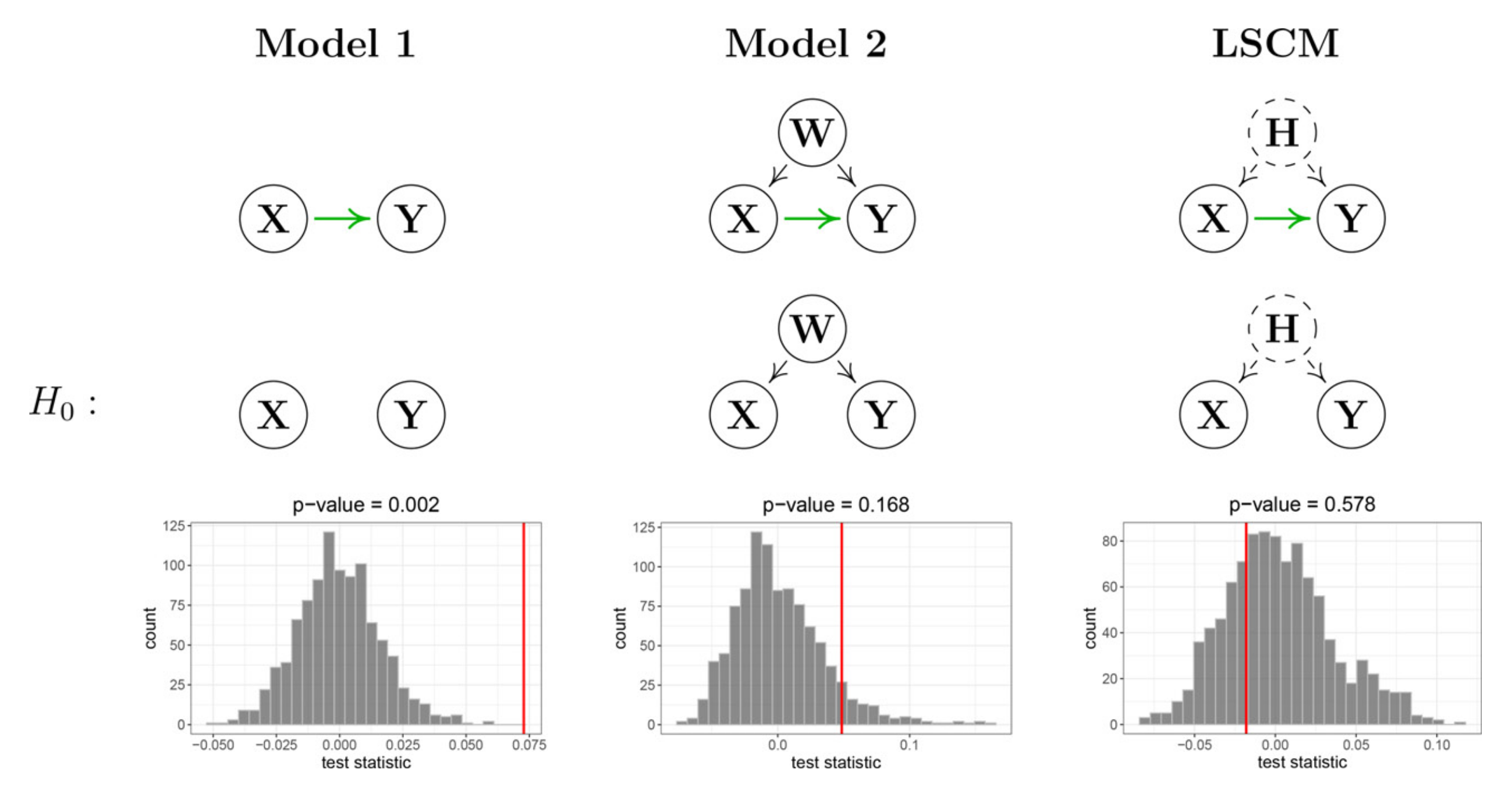 논문에서 보인 검정 결과
논문에서 보인 검정 결과
앞서 논문에 사용된 conflict vs. forest loss 데이터에 대해 다음과 같은 변수 표기를 사용하였습니다.
- $X^{t}_{s}$ : 처치변수 (conflict)로서 시점 $t$에서의 격자 $s$에 대한 값
- $Y^{t}_{s}$ : 결과변수 (forest loss)로서 시점 $t$에서의 격자 $s$에 대한 값
- $W^{t}_{s}$ : 공변량 (distance to road)로서 시점 $t$에서의 격자 $s$에 대한 값
위 그림은 논문에서 제안한 방법론을 통해 검정한 결과입니다. 왼쪽은 $X,Y$ 두 변수만 이용해 단순한 검정을 수행한 결과이며, 가운데는 $W$를 추가하여 검정한 결과를, 오른쪽은 $X,Y$와 관측되지 않는 time-invariant한 잠재변수 $H$를 추가하여 검정한 결과입니다.
두 변수만 이용해 추정한 결과는 양의 효과($+0.073$)와 유의성($p=0.002$)을 보였으나, 공변량 $W$를 추가한 결과는 인과관계가 유의하지 못함을 보였습니다. 특히, 잠재변수 $H$를 추가한 결과는 인과관계가 유의하지 않음과 인과효과가 음($-0.018$)임을 보였습니다. 즉, 단순히 처치변수와 결과변수만 두고 인과관계를 추정했을 때는 잘못된 결론을 내릴 수 있음을 보여줍니다.
논문의 사회과학적 배경과 함의에 대한 자세한 설명은 논문을 참고하시기 바랍니다.
References
- R. Christiansen, Baumann ,Matthias, Kuemmerle ,Tobias, Mahecha ,Miguel D., and J. and Peters, “Toward Causal Inference for Spatio-Temporal Data: Conflict and Forest Loss in Colombia,” Journal of the American Statistical Association, vol. 117, no. 538, pp. 591–601, Apr. 2022, doi: 10.1080/01621459.2021.2013241.
Leave a comment