공간 데이터에서의 인과추론 : (3) 베이지안

저번 글에 이어, 이번 글에서도 공간 데이터의 인과추론에 대해 다루고자 합니다. 이번 글에서는 공간통계와 단짝이라고도 할 수 있는 베이지안 방법론을 기반으로 한 Spatial causal inference in the presence of unmeasured confounding and interference 논문을 소개합니다. 이 논문에서는 공간 인과 그래프^{spatial causal graphs}를 도입하여 confounder 및 interference의 존재를 설명하고 있습니다. 또한, 공간적 의존성을 고려하지 않은 인과적 분석이 잘못된 결론을 초래할 수 있음을 보여주고, 이를 해결하기 위한 베이지안 모형을 제안합니다.

Spatial Causal Graphs

이 논문에서는 spillover effect를 고려하기 위해 다음과 같은 표기를 사용합니다. 우선, 처치변수 $Z$가 $0,1$의 값만을 갖는 이진 변수이며 두 개의 unit이 존재하는 경우($i,j$)를 고려합시다. 이때 $Y_i$는 $i$번째 unit의 결과변수를 나타내는데, 구체적으로는 다음과 같이

\[Y_i(z_i,z_j)\]

로 표기합니다. 이는 $i$번째 개체의 결과변수가 $i$번째 개체의 처치변수 $Z_i$ 뿐만 아니라 다른 위치에 있는 $j$ 개체에 의해서도 영향을 받을 수 있음을 나타냅니다. 이러한 상황을 spatial interference라고 하며, 이는 SUTVA 가정의 no interference 조건을 위반하는 것이기도 합니다.

또한, 다음과 같이 지역 효과^{local effect} $\lambda_i$와 간섭 효과^{interference effect} $\iota_{ij}$를 도입합니다.

\[\begin{align*} \lambda_i(z) &= \mathbb{E}[Y_i(z_i=1, z_j=z_j)] - \mathbb{E}[Y_i(z_i=0, z_j=z_j)] \\ \iota_{i}(z) &= \mathbb{E}[Y_i(z_i=z, z_j=1)] - \mathbb{E}[Y_i(z_i=z, z_j=0)] \end{align*}\]

Observed pair data and causal identifiability

이 논문에서는 관측된 데이터가 쌍(pair) 형태로 주어졌다고 가정합니다. $\mathbf{Z}=(Z_1, Z_2)$와 $\mathbf{Y}=(Y_1, Y_2)$로 이루어진 쌍 데이터는 각각 처치변수와 결과변수를 나타내고 공변량 $\mathbf{U}=(U_1, U_2)$는 unmeasured confounder로 가정합니다. 이때, 다음과 같이 두 성질을 가정합니다.

No unmeasured confounding
\[\mathbf{Z} \perp Y_i(z_1,z_2) | \mathbf{U}\]
Ignorability
\[P_{\mathbf{Z}|\mathbf{u}}(\mathbf{z}|\mathbf{U}=\mathbf{u}) > 0\]

Causal DAG for spatial data

DAG는 인과관계를 설명하는데 효과적인 도구입니다. 이 논문에서는 공간적 의존성을 고려하기 위해 DAG를 기반으로 한 spatial causal graph를 도입합니다. 우선, pair 단위의 변수 $\mathbf{Z}, \mathbf{Y}, \mathbf{U}$에 대해서는 다음과 같은 DAG를 고려합니다.

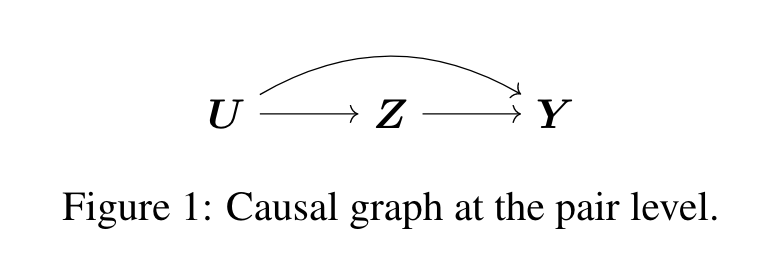
그런데, 공간 데이터 관점에서 살펴보면 아래와 같이 세 가지 경우를 생각할 수 있습니다. 이 논문에서는 두번째 경우인 (b)를 상정하며, 여기에서는 공간 간 간섭이 각 변수 수준에서는 존재하고 (양쪽방향 화살표), 간섭 효과($Z_{1}\to Y_{2}$ 등)이 존재하지만 confounder 수준에서의 간섭효과($U_{1}\to Z_{2}$)는 존재하지 않는다고 가정합니다. 또한, confounder 변수 $\mathbf{U}$ 내에서의 공간 종속성이 존재하고($U_{1}\leftrightarrow U_{2}$) 이를 spatial confounding이라고 합니다.

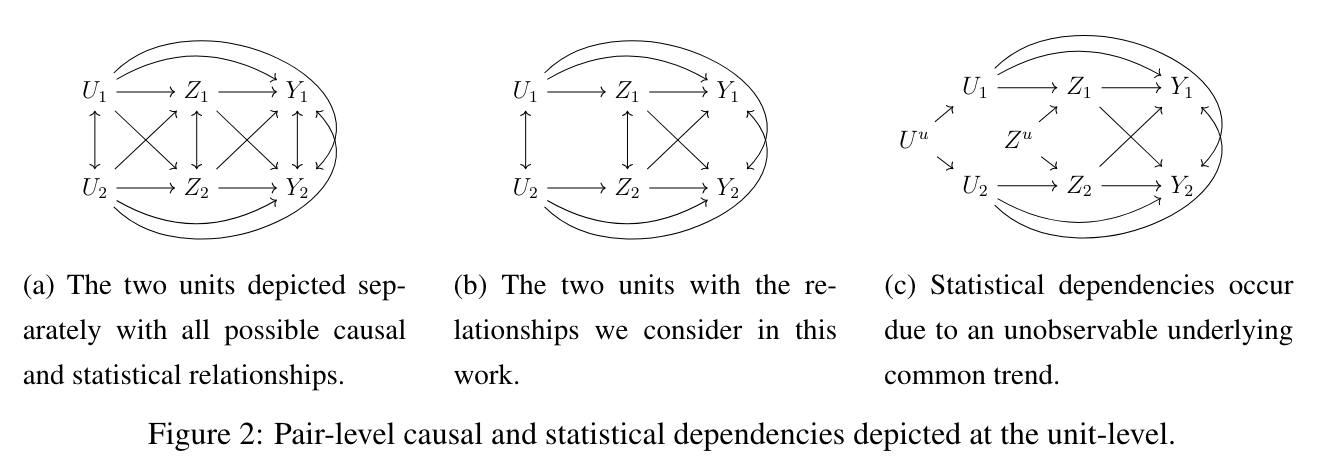
구체적으로는, (b)의 가정 상황에 대해 다음과 같이 6가지의 시나리오들을 고려할 수 있습니다. 각각의 시나리오에 대한 설명은 논문을 참고하면 될 것 같습니다.

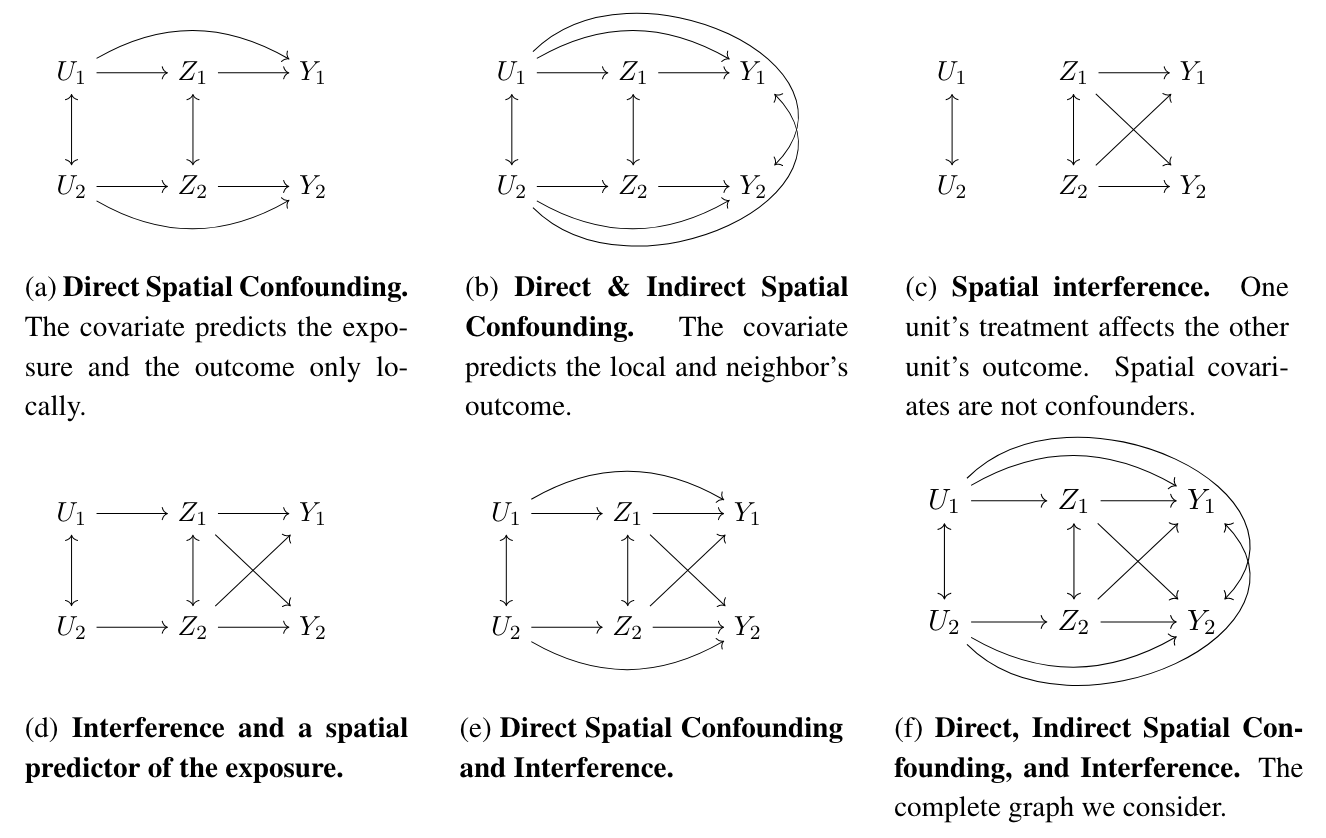
Causal Inference

위에서는 공간 데이터에 대해 인과모형을 어떤 구조로 가정할지에 대해 이야기했다면, 이번에는 구체적으로 데이터로부터 인과효과를 추정하는 과정에 대해 살펴보도록 하겠습니다.

Structural Equation Framework

인과효과의 추정을 위해 다음과 같이 SEM^{Structural Equation Model, 구조방정식} 모델을 사용합니다.

\[Y_{i}(z, \bar{z}) =f_{1}(z,\bar{z}) + f_{2}(\tilde{C}_{i}) + f_{3}(U_{i}, \bar{U}_{i}) + \epsilon_{i}(z,\bar{z}) \tag{1}\]

여기서 전체 개체(unit)의 수는 $i=1,\ldots,n$이고 $\tilde{C}_{i}$는 $i$번째 개체의 $p$개 공변량 $(C_{i1},\ldots,C_{ip})$를 나타냅니다. 또한, $\bar{z}$는 다음과 같이 정의됩니다($\bar U$도 마찬가지로 정의).

\[\bar{z}_{i} = \sum_{j=1}^{n} A_{ij}z_{j} / \sum_{j=1}^{n} A_{ij}\]

여기서 $A_{ij}$는 $i$번째 개체와 $j$번째 개체 간의 공간적 관계를 나타내는 adjacency matrix입니다. Areal data의 경우는 두 개체가 인접한 경우에 $A_{ij}=1$로 설정하고, 그렇지 않은 경우는 $A_{ij}=0$으로 설정하는 것이 일반적이며, point data의 경우는 두 개체간의 거리로 $A_{ij}$를 정의할 수 있습니다. 즉, 이는 인접한 요인들의 가중평균을 나타냅니다. 또한, 오차항 $\epsilon_{i}(z,\bar z)$는 서로 독립이고 평균이 $0$, 분산이 $\sigma_{Y}^{2}$인 분포를 가정합니다.

위 SEM (1)에서 각 함수에 선형 형태를 가정한다면(가장 일반적인 구조방정식 가정), 식 (1)은 다음과 같이 간단하게 표현됩니다.

\[Y_{i}(z,\bar z) = \beta_{0}+\beta_{Z}z + \beta_{\bar Z}\bar{z} + \tilde{C}_{i}^{T}\boldsymbol{\beta}_{C}+ \beta_{U}U_{i} + \beta_{\bar U}\bar U_{i}+\epsilon(z,\bar z)\]

이때, $\beta_{Z}$는 local effect, $\beta_{\bar Z}$는 interference effect에 각각 대응됩니다. 구체적으로, local effect $\beta_{Z}$는 이웃 개체들의 처치가 고정된 상태에서 $i$번째 개체의 처치가 결과변수에 미치는 영향을 나타내고, interference effect $\beta_{\bar Z}$는 $i$번째 개체의 처치가 고정된 상태에서 이웃 개체들의 처치가 결과변수에 미치는 영향을 나타냅니다.

Bayesian Causal Inference

앞선 구조방정식 기반 모델에서는 만일 측정된 공변량^covariates들이 충분하지 않아 confounding adjustment, 즉 공변량이 주어진 경우에서의 조건부 독립성이 충족되지 않을 경우 추정된 인과효과에 편향^bias이 발생하게 됩니다. 이를 해결하기 위해 논문에서는 베이지안 인과추론을 도입하여 공간 구조에서의 인과추론을 수행합니다. 베이지안 인과추론은 관측되지 않은 potential outcome(한 개체가 처치 집단에 속한다면, 그 개체가 처치되지 않은 경우의 결과값)을 결측치^{missing data}로 보고 사후분포를 바탕으로 인과효과를 추정합니다.

앞선 세팅에서 추가로, $\mathbf{Y}(\cdot) = {\mathbf{Y},\mathbf{Y}^\text{miss}}$를 설정하는데 이는 관측된 결과변수 $\mathbf{Y}$와 관측되지 않은 결과변수(결측치) $\mathbf{Y}^\text{miss}$ 의 모임입니다. 이때 결측치의 사후분포는 다음과 같이 계산할 수 있습니다.

\[p(\mathbf{Y}^{\text{miss}} \mid \mathbf{Y},\mathbf{Z},\overline{\mathbf{Z}}, \mathbf{C},\theta) \propto P(\mathbf{Z,\overline{Z}}\mid\mathbf{Y}(\cdot), \mathbf{C},\theta)P(\mathbf{Y}(\cdot)\mid \mathbf{C},\theta)P(\mathbf{C}\mid \theta)\]

이때 $\theta$는 모델에 사용된 모수^parameter를 의미합니다. 여기서 주의할 점은, ignorability 가정이 측정된 공변량 $\mathbf{C}$로만은 성립하지 않기 때문에 이 경우 treatment assignment mechanism $P(\mathbf{Z,\overline{Z}}\mid\mathbf{Y}(\cdot), \mathbf{C},\theta)$ 을 위 식 (2)에서 분리할 수 없습니다. 따라서, 결측치만의 사후분포 대신 다음과 같이 전체 데이터에 대한 결합분포를 우선 고려합니다.

\[p(\mathbf{Y}(\cdot),\mathbf{Z,\overline Z}, \mathbf{C}) = \int p(\mathbf{Y}(\cdot)|\mathbf{Z}, \mathbf{C}, \mathbf{U},\theta^\ast) p(\mathbf{Z}|\mathbf{C,U},\theta^\ast)p(\mathbf{U}|\mathbf{C},\theta^\ast)d\mathbf{U} p(\theta^\ast) d\theta^\ast\]

여기서 $\overline{\mathbf{Z}}$는 $\mathbf{Z}$의 평균으로 정의되었기 때문에, $\mathbf{Z}$에 의해 유일하게 결정되므로 위 식에서 제거되었고 $\theta^\ast$는 $\theta$와 $\mathbf{U}$의 모수들을 모두 포함하는 모수입니다.

앞서 살펴본 SEM 식 (1)에서는 서로 다른 개체들의 결과변수들이 나머지 정보가 주어진 경우 독립적으로 가정했으므로 위 식은 다음과 같이 unit-wise로 나누어 표현할 수 있습니다.

\[\begin{align*} p(\mathbf{Y}(\cdot)|\mathbf{Z}, \mathbf{C}, \mathbf{U},\theta) &= \prod_{i=1}^{n} p(Y_{i}(\cdot)|Z_i, \bar Z_i, \tilde C_i, U_i, \bar U_i,\theta)\\ &= \prod_{i=1}^{n} p(Y_{i}(\cdot)|\tilde C_i, U_i,\bar U_i,\theta) \end{align*}\]

결과적으로 앞선 결합분포$ $p(\mathbf{Y}(\cdot),\mathbf{Z,\overline Z}, \mathbf{C})$는 다음과 같이 표현할 수 있습니다.

\[\int \left(\prod_{i=1}^{n} p(Y_{i}(\cdot)|\tilde C_i, U_i,\bar U_i,\theta)\right) p(\mathbf{Z}|\mathbf{C,U},\theta)p(\mathbf{U}|\mathbf{C},\theta)d\mathbf{U} p(\theta) d\theta\]

위 식으로부터 얻을 수 있는 인사이트는, 관측되지 않은 공변량 $\mathbf{U}$가 treatment assignment mechanism $P(\mathbf{Z}\mid\mathbf{C,U},\theta)$에 영향을 미치기 때문에, 이 역시 베이지안 모델에 포함되어야 한다는 것입니다. 즉, 단순히 결과 모델에 spatial random effect를 도입하는 것으로는 충분하지 않으며, treatment assignment mechanism에도 spatial random effect를 도입해야 한다는 것입니다.

Exposure-confounder assumptions

이를 해결하기 위해 논문에서는 다음과 같은 분포 가정을 제안합니다.

\[\begin{pmatrix} \mathbf{U} \\ \mathbf{Z} \end{pmatrix} \mid \mathbf{C} \sim \mathcal{N}_{2n} \left( \begin{pmatrix} \mathbf{0}_n \\ \gamma_0 \mathbf{1}_n + \mathbf{C}\boldsymbol{\gamma}_C \end{pmatrix}, \begin{pmatrix} G & Q \\ Q^T & H \end{pmatrix}^{-1} \right)\]

여기서 $Q$는 대각행렬로 원소 $q_i=-\rho\sqrt{g_{ii}h_{ii}}$로 정의됩니다. 이로 인해 $\mathbf{U}$와 $\mathbf{Z}$는 서로 독립적이지 않지만, precision matrix를 통해 조건부 독립을 만족합니다. 즉, 다음이 성립합니다.

\[Z_i \perp \mathbf{U}_{-i} | U_i, \mathbf{Z}_{-i}, \mathbf{C}\]

여기서 $\mathbf{U}_{-i}$는 $i$번째 개체를 제외한 나머지 개체들의 공변량을 의미합니다. 이러한 조건부 독립이 precision matrix에서 $Q$를 대각행렬로 가정하며 유도된 것입니다.

또한, 실제로는 처치변수 $\mathbf{Z}$에 대해 하나의 데이터셋만을 관측할 수 있기 때문에, precision matrix $G$와 $H$를 추정하기 위해서는 추가적인 구조 가정이 필요합니다. 여기서는 다음과 같이 파라미터들을 설정합니다.

\[\begin{align*} G &= \tau_U^2 (D-\phi_U A) \\ H &= \tau_Z^2 (D-\phi_Z A) \\ \theta_U &= (\tau_U^2, \phi_U) \\ \theta_Z &= (\tau_Z^2, \phi_Z) \end{align*}\]

여기서 $D$는 대각행렬로 원소 $d_{ii}=\sum_{j=1}^{n} A_{ij}$로 정의됩니다. 물론 precision matrix의 모델이 위와 같이 반드시 설정되어야 할 필요는 없지만, 위는 일반적으로 공간통계에서 Gaussian Markov random field를 다룰 때 사용되는 형태의 모델입니다.

이러한 설정을 통해, MCMC나 VI^{Variational inference} 등 베이지안 추론 방법을 사용하여 local effect $\beta_{Z}$와 interference effect $\beta_{\bar Z}$를 추정할 수 있습니다. 구체적인 모형은 논문을 참고하시면 좋을 것 같습니다.

References

G. Papadogeorgou and S. Samanta, “Spatial causal inference in the presence of unmeasured confounding and interference,” Feb. 02, 2024, arXiv:2303.08218. doi: 10.48550/arXiv.2303.08218.