Graph Clustering

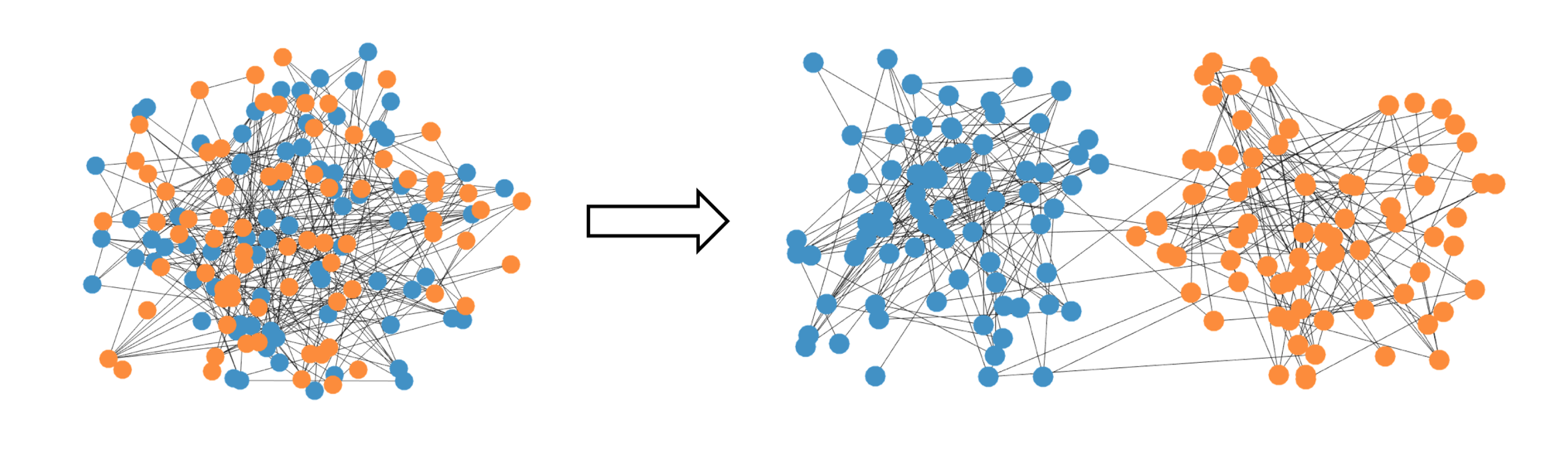Graph Clustering

Graph Clustering(혹은 community recovery)란, 위 그림과 같이 그래프의 노드들을 서로 다른 커뮤니티(그룹)으로 나누는 방법론을 의미한다. 특히 소셜 미디어의 발달로 인해 최근 들어 개인간 연결성이 강조되며, SNA(social network analysis) 영역에서 주로 연구되는 방법론이며, 컴퓨터 비전이나 의학통계 영역에서도 많이 사용된다고 한다. 일반적으로 graph clustering은 stochastic block model을 기반으로 이루어지는데, 이에 대해 다루어보도록 하겠다.

Stochastic block model

Problem Formulation

그래프 $\mathcal{G}=(V,E)$ 가 주어지고 $V$는 n개의 노드(node, 혹은 vertex)의 집합을, $E$는 변(edge)들의 집합을 각각 나타낸다고 하자. $n$은 짝수로 주어지고, 전체의 절반 노드씩 서로 다른 그룹 $\lbrace +1,-1\rbrace $ 에 속한다고 하자. 즉, 각 노드의 그룹을 나타내는 변수를 다음과 같이 정의하자.

\[x_{i}^{\star}=\begin{cases} 1, \quad\quad \text{if vertex $i$ belong to the 1st community} \\ \\ -1,\quad \text{ otherwise} \end{cases}\]

Stochastic block model(SBM)은 edge set $E$가 주어진 $x_{i}^{\star}$ 들을 바탕으로 랜덤하게 생성된다고 가정한다. 엄밀히 정의하면, 그래프의 각 변 $(i,j)$은 만일 $i,j$ 번째 노드가 같은 그룹에 속하면 확률 $p$로 연결되고, 다른 그룹에 속하면 확률 $q=1-p$로 연결된다. 즉, 다음과 같다.

\[\begin{cases} P((i,j)\in E) = p,\quad\text{if i,j in same community} \\ \\ P((i,j)\in E) = q,\quad\text{else} \end{cases}\]

또한, 이렇게 정의된 그래프 $\mathcal{G}$에 대해 다음과 같이 adjacency matrix $A$를 정의하자.

\[A_{i,j}=\begin{cases} 1,\quad\text{if}\;(i,j)\in E \\ \\ 0,\quad\text{otherwise} \end{cases}\]

이렇게 정의된 adjacency matrix $A$를 SBM에 의해 생성되었다고 표현한다. Graph clustering의 목표는 $A$를 바탕으로 각 노드의 latent community membership, 즉 $x_{i}^{\star}$ 들을 추정하는 것이다. 결국 관측 행렬을 바탕으로 perturbation이 제거된 기대 행렬을 추정하는 문제로 귀결되므로, 우리는 앞서 다룬 spectral analysis를 이용할 수 있다.

Algorithm

Idea

일반성을 잃지 않고, 두 노드 그룹이 $i=1,\ldots,\frac{n}{2}$ 에 대해 $x_{i}^{\star}=1$ 로 주어지고, $i>\frac{n}{2}$ 에 대해서는 $x_{i}^{\star}=-1$ 로 주어진다고 하자. 이로부터 생성된 SBM의 adjacency matrix를 생각해보면, 우리는 각 변이 생성될 확률을 알고 있으므로(앞선 정의로부터) 다음과 같이 기댓값을 취할 수 있다.

\[\mathbb{E}A=\begin{bmatrix} p\mathbf{1}_\frac{n}{2}\mathbf{1_\frac{n}{2}}^{T} & q\mathbf{1}_\frac{n}{2}\mathbf{1_\frac{n}{2}}^{T} \\ q\mathbf{1}_\frac{n}{2}\mathbf{1_\frac{n}{2}}^{T} & p\mathbf{1}_\frac{n}{2}\mathbf{1_\frac{n}{2}}^{T}\end{bmatrix} - p\mathbf{I}_{n}\]

그런데, 이는 다음과 같이 변형가능하다.

\[= \frac{p+q}{2} \mathbf{J}_{n} + \frac{p-q}{2}\begin{pmatrix} \mathbf{1}_{n/2} \\ -\mathbf{1}_{n/2}\end{pmatrix} \begin{pmatrix}\mathbf{1}_{n/2}^T&-\mathbf{1}_{n/2}^{T}\end{pmatrix}-p\mathbf{I}_{n}\]

이때 행렬 $M,M^{\star}$를 다음과 같이 정의하면

\[M= A- \frac{p+q}{2}\mathbf{J}_{n}+p\mathbf{I}_{n}\tag{1}\] \[M^{\star}:=\mathbb{E}M=\frac{p-q}{2}\begin{pmatrix} \mathbf{1}_{n/2} \\ -\mathbf{1}_{n/2}\end{pmatrix} \begin{pmatrix}\mathbf{1}_{n/2}^T&-\mathbf{1}_{n/2}^{T}\end{pmatrix}\]

행렬 $M^{\star}$의 계수가 1이기 때문에 $M$역시 low rank(rank 1) approximation으로 볼 수 있다. 또한, $M^{\star}$의 leading eigenvalue와 leading eigenvector는 다음과 같이 주어진다.

\[\lambda^{\star}:=\frac{(p-q)n}{2},\quad u^{\star}:=\frac{1}{\sqrt{n}}\begin{bmatrix} \mathbf{1}_{n/2} \\ \mathbf{-1}_{n/2} \end{bmatrix}\]

이때 eigenvector $u^{\star}$는 $p,q$에 무관하게 우리가 찾고자 하는 community structure $x_{i}^{\star}$를 반영한다는 것을 파악할 수 있다.

Algorithm

위 아이디어로부터, 다음과 같은 간단한 graph clustering 알고리즘을 생각할 수 있다.

  1. 주어진 adjacency matrix $A$에 대해 $M$의 (식 1) leading eigenvector $u$를 계산한다.
  2. latent community membership $x_{i}$들을 다음과 같이 추정한다. \(x_{i}=\mathrm{sgn}(u_i)=\begin{cases} 1,\quad \;\;\mathrm{if}\; u_{i}>0 \\ -1,\quad \mathrm{if}\; u_{i}\leq 0 \end{cases}\)

즉, 행렬 $M$의 leading eigenvector를 구하는 것만으로도 그래프의 커뮤니티 관계를 파악할 수 있다는 것이다.

Performance

Lemma

이전 spectral analysis 방법론들과 마찬가지로 David-Kahan $\sin\Theta$ theorem 을 사용하기 위해 우선 perturbation matrix $E$의 크기를 제한해야 한다. 이는 다음 lemma로부터 얻을 수 있다.

$np\gtrsim \log n$ 인 경우 확률 $1-O(n^{-8})$ 으로 다음이 성립한다.

\[\Vert E\Vert\lesssim \sqrt{np}\]

이를 이용하면, David-Kahan theorem 으로부터 위 Graph clustering 알고리즘의 정확성에 대해 다음과 같은 정리가 성립한다.

Theorem

우선, 다음을 가정하자.

\[p\gtrsim \frac{\log n}{n},\quad \sqrt{\frac{p}{n}}=o(p-q)\]

그러면 확률 $1-O(n^{-8})$ 으로 위 graph clustering 알고리즘에 대해 다음이 성립한다.

\[\frac{1}{n}\sum_{i=1}^{n}\mathbb{1}(x_{i}=x_{i}^{\star})=1-o(1)\]

즉, 알고리즘의 정확성(맞게 분류한 노드 수/전체 노드 수)이 $n$이 커짐에 따라 1로 수렴한다는 것이다.

Example

Python의 networkx 패키지를 이용하여 다음과 같이 SBM을 생성하였다.($n=40,p=0.8,q=0.2$)

sizes = [20,20]
p, q = 0.8, 0.2
probs = [[p, q], [q, p]]
G = nx.stochastic_block_model(sizes, probs, seed=0)
pos = nx.spring_layout(G, seed=0)

Adjacency matrix A와 이를 바탕으로 다음과 같이 leading eigenvector를 계산하였다.

# Get Adjacency Matrix
A = nx.adjacency_matrix(G).todense()
A = np.array(A)

# define M
M = A - (p+q) / 2 * np.ones((40,40)) - p * np.eye(40)

# get the leading eigenvector
eigvals, eigvecs = np.linalg.eig(M)
leading_eigvec = eigvecs[:, 0]

## Result
array([-0.10430201, -0.14665696, -0.15684866, -0.148169  , -0.08294298,
       -0.10233172, -0.17420647, -0.22132117, -0.16244942, -0.15939122,
       -0.10899867, -0.16673839, -0.11381127, -0.20133096, -0.18587153,
       -0.12504019, -0.08759211, -0.17772523, -0.21765058, -0.16025109,
        0.20945734,  0.14203171,  0.18534778,  0.1335954 ,  0.16392122,
        0.10654508,  0.16734306,  0.16085389,  0.18285309,  0.14668154,
        0.12751267,  0.16584503,  0.15150189,  0.16003915,  0.16969697,
        0.18510644,  0.12769879,  0.20372017,  0.15294653,  0.1304846 ])

분석 결과 실제로 노드 0-19까지에 해당하는 고유벡터 성분은 음수로, 20-39까지의 고유벡터 성분은 양수로 나타나 clustering이 잘 이루어졌음을 확인할 수 있다.

References

  • Yuxin Chen et al. - Spectral Methods for Data Science: A Statistical Perspective (2021)

Leave a comment