Transformer
Transformer
(Updated on 2024-04-12)
트랜스포머Transformer는 자연어 처리 분야에서 최근 주를 이루고 있는 딥러닝 모델이다. 이전까지는 LSTM 등의 순환신경망을 주로 이용했지만, sequence-to-sequence function approximation에서 대형 트랜스포머들이 좋은 성능을 보이는 것이 알려지며 주요 모델로 자리잡게 되었다. 트랜스포머의 전반적인 구조는 다음과 같다.
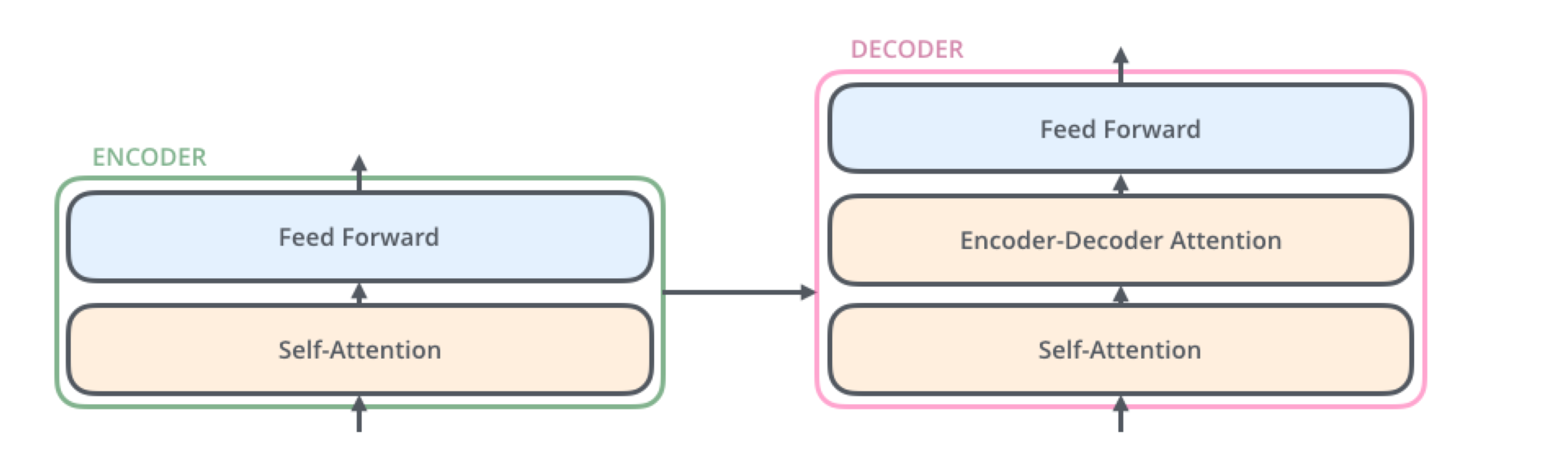
오토인코더 등과 비슷하게 인코더와 디코더로 이루어졌지만 모델에서의 계산 방식은 사뭇 다르다. 이번 포스트에서는 트랜스포머의 동작 원리를 자세하게 다루어보고자 한다.
Transformer block
트랜스포머는 block 단위의 연산을 sequential하게 적용하여 결과를 도출해낸다. Input $X^{(0)}\in \mathbb{R}^{D\times N}$ 에 대한 output은 다음과 같다. 여기서 $D$는 차원, $N$은 토큰의 개수(length of sequence)를 의미한다.
\[X^{(M)} = T_{M}\circ T_{M-1}\circ\cdots\circ T_{1}(X^{(0)}).\]각각의 Transformer block $T_{m}$에는 self-attention 등의 연산이 포함된다. 이때, 데이터 $X$의 열벡터 $\mathbf{x}_{i}\in \mathbb{R}^{D}$ 들을 token이라고 한다.
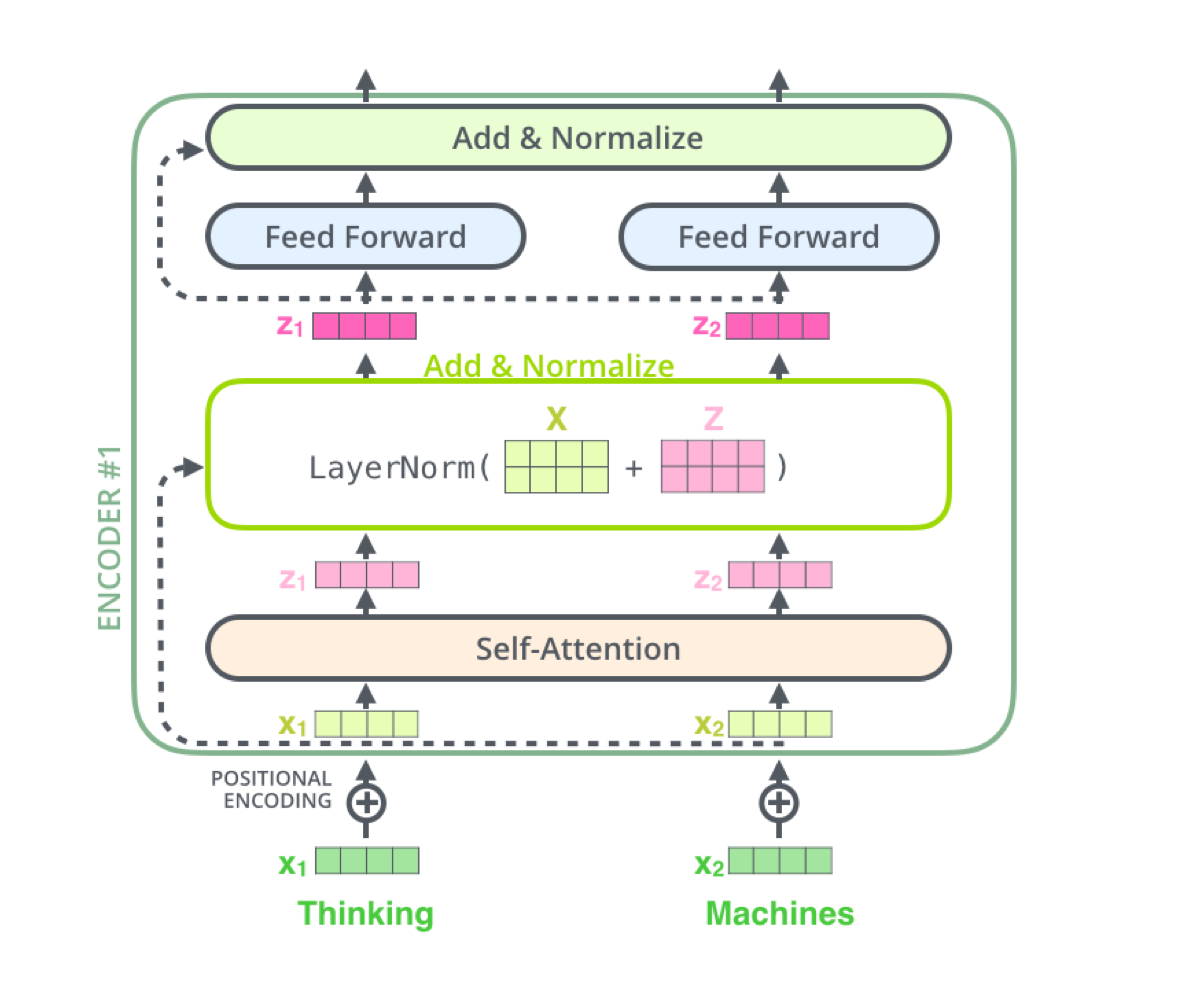
위 그림은 transformer block의 연산 구조를 나타낸다. 각각의 transformer block에는 다음 연산들이 존재한다.
- Self-attention
- Multi-head self-attention
- Layer Normalization
- Residual connection
Self-attention
Attention
Attention을 간단히 정의해보면, 입력 벡터들의 가중평균이다. $m$ 시점의 transformer block에서, $n$번째 output token $\mathbf{y}_{n}^{(m)}$는 다음과 같이 계산된다.
\[\mathbf{y}_{n}^{(m)} = \sum_{n^{\prime}=1}^{N} \mathbf{x}_{n^{\prime}}^{(m-1)}A_{n^{\prime},n}^{(m)}\]여기서 $A^{(m)}\in \mathbb{R}^{N\times N}, \sum_{n’=1}^{N}A_{n’,n}^{(m)}=1$ 는 attention matrix 라고 부른다. 이를 행렬로 표현하면 다음과 같다.
\[Y^{(m)}=X^{(m-1)}A^{(m)}\]직관적으로 생각해보면, attention matrix의 $(p,q)$ 성분이 높은 값을 갖는다는 것은 토큰에서 $p,q$ 번째 위치가 높은 관련성을 갖는다는 것을 의미한다.
Self-attention
Self-attention이란, attention matrix를 입력 데이터로부터 구성하는 방법이다. 구성은 다음과 같이 이루어진다.
\[A_{n.n'} = \dfrac{\exp(\mathbf{x}_{n}^{\top}U_{k}^{\top}U_{q}\mathbf{x}_{n'})}{\sum_{n''=1}^{N}\exp(\mathbf{x_{n''}}^{\top}U_{k}^{\top}U_{q}\mathbf{x}_{n'})}\]이때 다음과 같이 용어를 정의한다.
\[\begin{aligned} \text{query} & : \mathbf{q}_{n}= U_{q}\mathbf{x}_{n}\\ \text{key} & : \mathbf{k}_{n}= U_{k}\mathbf{x}_{n} \end{aligned}\]$A$의 계산 과정의 분모에서 $U_k^\top U_q$가 계산되므로 query와 key의 차원이 $d_K$로 같아야 한다. 즉, $U_q,U_k \in \mathbb{R}^{d_K \times D}$ 이다.
위 Attention matrix를 계산하는 과정에서, 차원에 대한 의존성을 줄이기 위해 다음과 같이 일종의 normalization을 취하기도 한다.
\[A_{n.n'} = \dfrac{\exp(\mathbf{x}_{n}^{\top}U_{k}^{\top}U_{q}\mathbf{x}_{n'}/\sqrt{d_K})} {\sum_{n''=1}^{N}\exp(\mathbf{x_{n''}}^{\top}U_{k}^{\top}U_{q}\mathbf{x}_{n'}/\sqrt{d_K})}\]이러한 형태로 구성되는 Attention을 scaled dot-product attention이라고 부른다. $\sqrt{d_K}$로 나누어주는 이유는, 차원이 커질수록 내적값이 커지기 때문에, 이를 방지하기 위함이다. 이를 직관적으로 이해하면 다음과 같다.
$(\mathbf q_n)_r \sim N(0,1)$ 이라고 하면,
\[\begin{aligned} {\rm Var}(\mathbf q_i^\top \mathbf k_j) &= \sum_{r=1}^{d_K} {\rm Var}((\mathbf q_n)_r (\mathbf k_n)_r)\\ &= \sum_{r=1}^{d_K} {\rm Var}((\mathbf q_n)_r) {\rm Var}((\mathbf k_n)_r)\\ &= d_k \end{aligned}\]따라서, ${\rm Var}(d_K^{-1/2} \mathbf q_i^\top \mathbf k_j) = 1$ 이 되도록 scaling을 해주는 것이다.
Self-attention vs RNN
순환신경망Recurrent neural network. RNN에서는 hidden state update가 다음과 같이 이루어진다.
\[\mathbf{x}_{n}^{(1)}=f_{\theta}\left(\mathbf{x}_{n-1}^{(1)};\mathbf{x}_{n}^{(0)}\right)\]위 식을 한번 더 풀어서 작성하면 다음과 같은데,
\[\mathbf{x}_{n}^{(1)}=f_{\theta} \left(f_{\theta}\left(\mathbf{x}_{n-2}^{(1)};\mathbf{x}_{n-1}^{(0)}\right);\mathbf{x}_{n}^{(0)}\right)\]$n$번째 토큰의 업데이트 과정에서 이전 단계의 $n-1$번째 토큰과 $n$번째 토큰이 다른 영향을 주게 된다. 구체적으로, 거리가 먼 토큰일수록 업데이트에 미치는 영향이 작아지게 된다.
반면, self-attention의 경우 각 업데이트 과정에서 모든 토큰을 동일한 attention matrix로 처리하기 때문에, 토큰의 거리와 관계없이 업데이트가 이루어진다. 이러한 특성으로 인해 long-range relationship 학습이 용이하며 특히 이는 자연어 학습에서 주요 강점으로 작용한다.
Multi-head self-attention (MHSA)
Multi-head self-attention이란, 여러 개의 self-attention 계산을 병렬적으로 처리하는 것을 의미한다. 다음과 같이 식으로 나타낼 수 있다.
\[Y^{(m)}= \text{MHSA}_{\theta}\left(X^{(m-1)}\right)=\sum_{h=1}^{H}V_{h}X^{(m-1)}A_{h}^{(m)}\]여기서 $A_{h}$는 다음과 같이 정의된다.
\[\left(A_{h}^{(m)}\right)_{n,n'} = \dfrac{\exp \left(\left(\mathbf{k}_{h,n}^{(m)}\right)^{\top}\mathbf{q}_{h,n'}^{(m)}\right)}{ \sum_{n''=1}^{N}\exp \left(\left(\mathbf{k}_{h,n''}^{(m)}\right)^{\top}\mathbf{q}_{h,n'}^{(m)}\right) }\]이때 query, key는 각각 다음과 같다.
\[\mathbf{q}_{h,n}^{(m)}=U_{q,h}^{(m)}\mathbf{x}_{n}^{(m-1)},\quad \mathbf{k}_{h,n}^{(m)}=U_{k,h}^{(m)}\mathbf{x}_{n}^{(m-1)}\]따라서, MHSA에서의 파라미터는 $\lbrace U_{q,h},U_{k,h},V_{h}\rbrace $ 로 구성된다.
Layer Normalization
Layer normalization은 신경망의 출력층을 다음과 같이 표준화하는 것을 의미한다.
\[\bar x_{d,n} = \text{LayerNorm}(X)_{d,n}= \frac{1}{\sqrt{\mathrm{Var}(\mathbf{x}_{n})}}\left(x_{d,n}- \frac{1}{D}\sum_{d=1}^{D}x_{d,n}\right)\]Layer normalization에서 주의할 것은, sequence의 토큰들에 대해 normalization을 수행하는 것이 아닌, 각 토큰의 차원에 대해 normalization을 수행한다는 것이다. 이는 batch normalization이나 CNN에서의 Layer normalization과 다른 점이다.
Encoder block
앞서 설명한 연산들을 종합하면, $m$번째 인코더 블록에서 이루어지는 연산을 다음과 같이 표현할 수 있다.
\[\begin{align} \bar X^{(m-1)}&= \text{LayerNorm}\left(X^{(m-1)}\right)\\ Y^{(m)}&= X^{(m-1)}+\text{MHSA}\left(\bar X^{(m-1)}\right)\\ \bar Y^{(m)}&= \text{LayerNorm}\left(Y^{(m)}\right)\\ X^{(m)}&= Y^{(m)}+\text{MLP}\left(\bar Y^{(m)}\right) \end{align}\]Positional Encoding
앞선 encoder block의 그림을 보면, input data에 positional encoding을 취한다고 표시된 것을 확인할 수 있다. Positional encoding이란, 각 토큰들에 대해 데이터에서의 위치정보를 부여하는 방식이다. 이는 특히 자연어 처리 문제에서 중요한데, 위치정보를 고려하지 않을 경우 다음과 같은 permutation 상황에서 문제가 발생할 수 있기 때문이다.
- 책 + 에 + 가방 + 을 + 넣었다.
- 가방 + 에 + 책 + 을 + 넣었다.
이를 해결하기 위해 각 input 토큰 $\mathbf{x}\in \mathbb{R}^{D}$ 에 대해 다음과 같이 위치정보를 나타내는 벡터를 추가할 수 있다.
\[\mathbf{x}_{n}^{(0)} \leftarrow \begin{align} \begin{pmatrix} \mathbf{x}_{n}^{(0)}\\ \mathbf{e}_{n}\end{pmatrix} \end{align}\]혹은, positional embedding vector $\lbrace p_l\rbrace \in \mathbb{R}^{D}$을 더해주는 방식으로도 사용된다. 즉,
\[\mathbf{x}_{n}^{(0)}\leftarrow \mathbf{x}_{n}^{(0)}+p_{l}\]이다.
NLP 분야에서는 다음과 같은 형태의 sinusoidal positional encoding을 사용하기도 한다. (Vaswani et al., 2017)
\[p_l = \begin{pmatrix} \sin(l/10000^{2\cdot 1/D})\\ \cos(l/10000^{2\cdot 1/D})\\ \vdots\\ \sin(l/10000^{2\cdot \frac{D}{2}/D})\\ \cos(l/10000^{2\cdot \frac{D}{2}/D}) \end{pmatrix}\]Vision transformer에서는 다음과 같은 선형변환을 사용하기도 한다. (Dosovitskiy et al., 2020)
\[\mathbf{x}_{n}^{(0)}=W\mathbf{p}_{n}+\mathbf{e}_{n}\]여기서 $\mathbf{p}_{n}=\text{vec(n-th patch)}$ 이고, $W$는 학습 가능한 파라미터이다. 즉, 위치정보를 나타내는 벡터를 학습을 통해 얻는다.
References
- Murphy, K. P. (2023). Probabilistic machine learning: Advanced topics. The MIT Press.
- Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., & Polosukhin, I. (2017, June 12). Attention Is All You Need. arXiv.Org. https://arxiv.org/abs/1706.03762v7
- Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer, M., Heigold, G., Gelly, S., Uszkoreit, J., & Houlsby, N. (2020, October 2). An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. International Conference on Learning Representations. https://openreview.net/forum?id=YicbFdNTTy
- https://jalammar.github.io/illustrated-transformer
- 서울대학교 딥러닝의 통계적 이해 강의노트
Leave a comment