Universal Approximation Theorem

딥러닝이 예측 문제에서 매우 높은 성능을 발휘하는 이유 중 하나는, 바로 딥러닝을 통해 근사한 함수가 보간^{interpolation}에 가깝게 원래 함수를 근사한다는 것이다. 바꾸어 말하면, 어떠한 함수든 신경망으로 근사할 수 있다는 것인데, 이러한 이론적 배경을 Universal Approximation Theorem이라고 한다.

ReLU

ReLU 활성함수는 단순히 0 이하의 부분을 cut-off 하는 간단한 활성함수지만, 이러한 특성으로 인해 역전파 알고리즘 단계에서 그래디언트 계산이 쉽고, 그래디언트 폭주 등 문제가 적다는 점에서 현재 대표적으로 이용되는 활성함수이다. Universal Approximation Theorem은 비단 ReLU 함수에만 적용되는 것은 아니지만, ReLU 함수를 이용해 살펴보면 좀 더 직관적인 이해가 가능하다.

우선, 1개의 hidden layer 층을 갖는 간단한 신경망 구조를 생각하자. 그리고 다음과 같이 hidden layer에 세 개의 노드가 있다고 가정하자. 아래 그림과 같다.

\[\begin{align} f_{1}(x) &= 0.25x+0.05 \\ f_{2}(x) &= x\\ f_{3}(x) &= -0.5x+0.25 \end{align}\]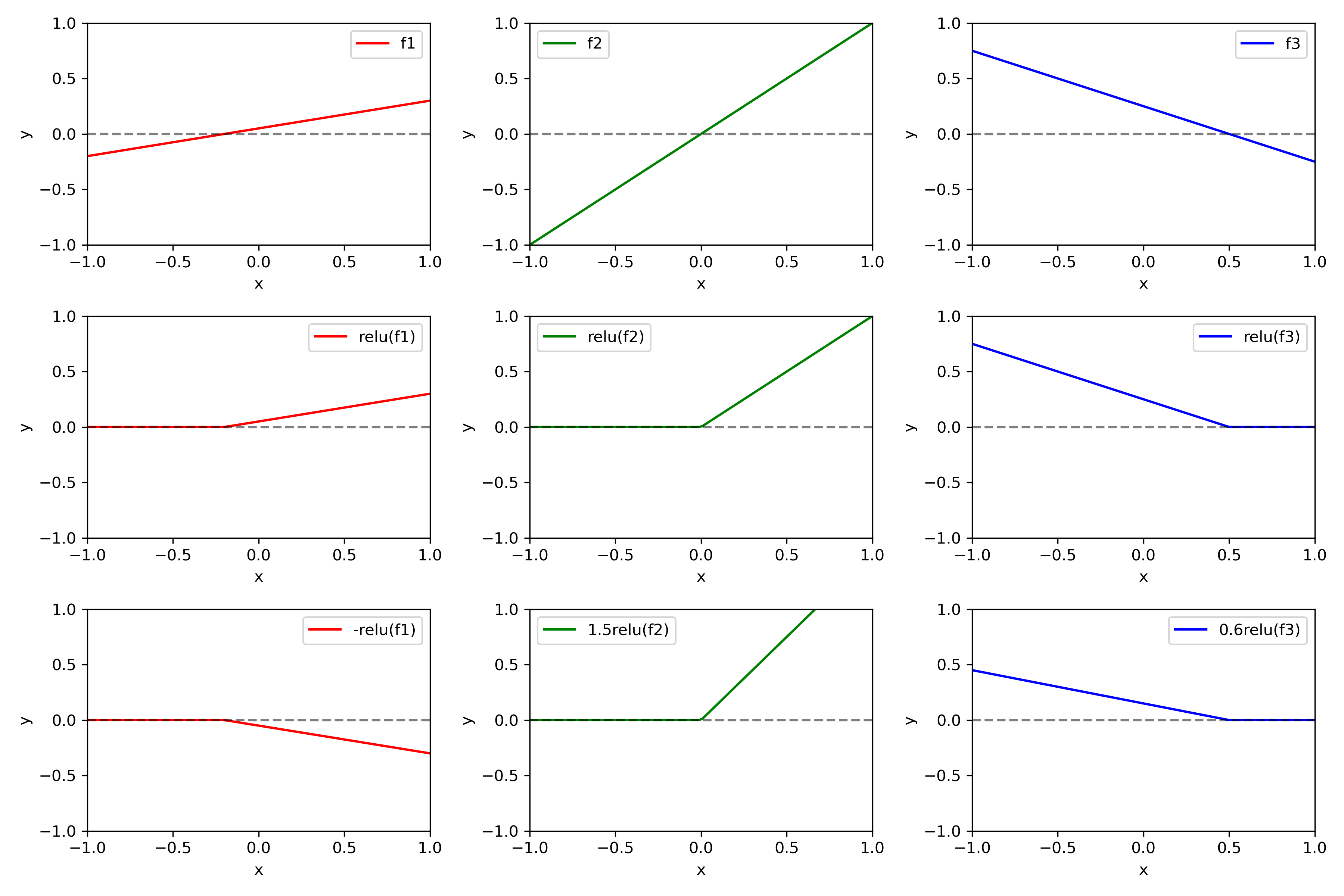

그렇다면 이들에 대해 ReLU함수를 취하고, 최종적으로 Output layer에 대해서는 다음과 같은 선형결합이 계산된다.

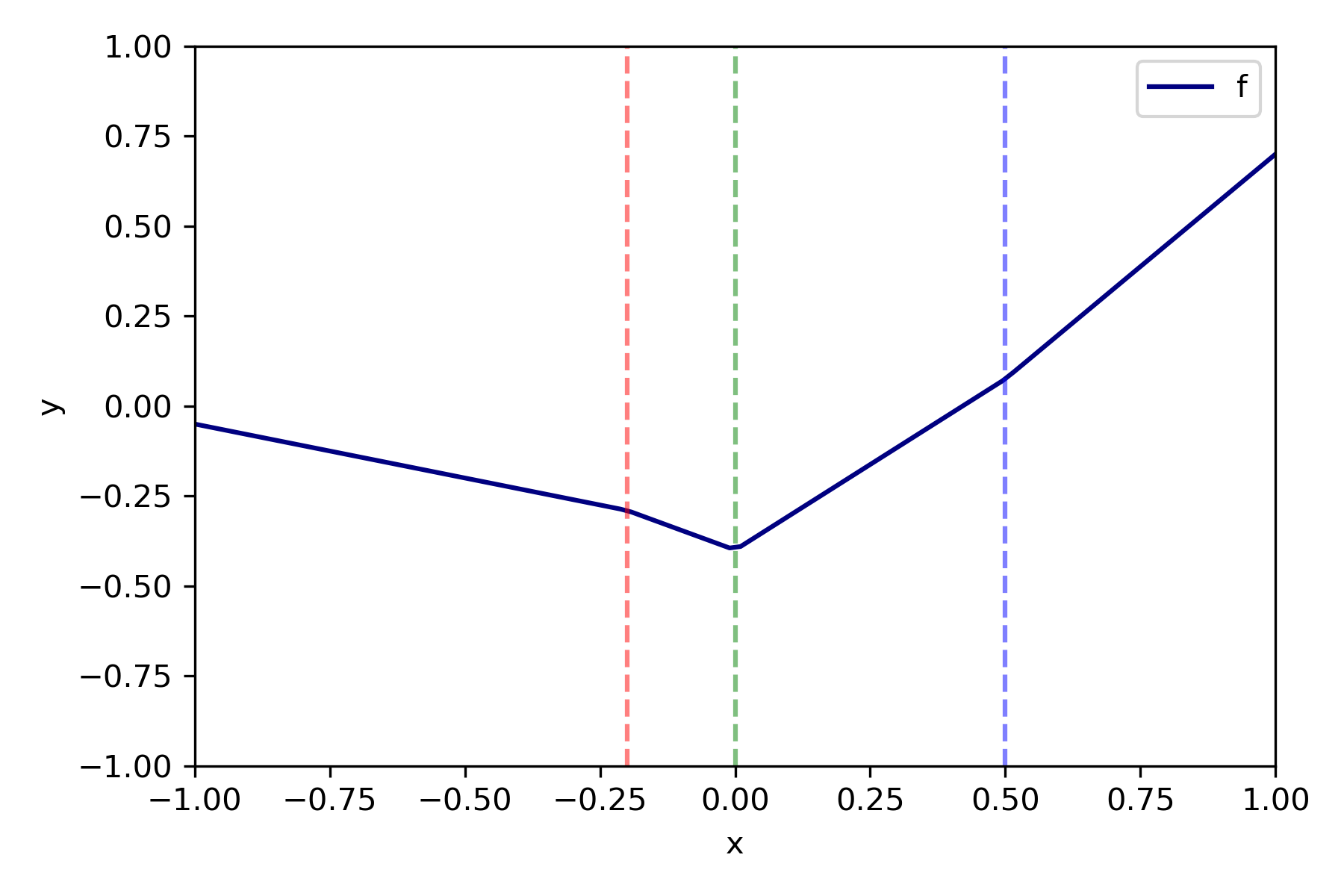
\[y = \phi_{0}+\phi_{1}\mathrm{ReLU}(f_{1}(x))+\phi_{2}\mathrm{ReLU}(f_{2}(x))+\phi_{3}\mathrm{ReLU}(f_{3}(x))\]

선형결합을 도식화하면, 다음과 같은 그래프를 얻을 수 있는데, 이는 마치 spline regression에서 매듭을 세개로 설정한 것과 같다. 즉, 은닉층의 각 노드가 매듭(수직 점선)에 대응된다. 이는 곧 은닉층의 노드 개수를 늘릴수록, 더 smooth한 함수를 만들 수 있다는 것이다. 이러한 아이디어를 이용하면, 임의의 함수를 아주 작은 간격의 선형함수들을 결합해 근사할 수 있다는 생각을 할 수 있는데, 이를 universal approximation theorem이라고 한다.

실제로, 완전연결 ReLU 신경망에 대해 다음과 같은 정리가 성립한다.

Theorem for Width-bounded ReLU

임의의 르벡적분가능한 $f:\mathbb{R}^{n}\to \mathbb{R}$ 과 임의의 양수 $\epsilon>0$ 에 대해, 너비^width가 $d_{m}\leq n+4$ 인 완전연결 ReLU 신경망 $F$가 존재하여 다음을 만족한다.

\[\int_{\mathbb{R^{n}}}\Vert f(x)-F(x)\Vert^{p}dx<\epsilon\]

즉, 다음이 성립한다는 것을 의미한다.

임의의 르벡적분가능한 함수에 대해, 미리 정해진 근사 정확도^{approximation accuracy}를 갖춘 너비 $n+4$ 의 ReLU 네트워크를 근사할 수 있다.

증명

위 정리의 증명은 임의의 르벡적분가능 함수 $f$를 $L^{1}$ 거리공간에서 근사하는 네트워크를 만드는 것이다. 증명의 순서는 다음과 같다.

$f$ 가 $n$차원 큐브에서 지시함수^{indicator function}들의 유한 가중합^{weighted sum}으로 나타낼 수 있다.

ReLU 네트워크가 $n$차원 큐브에서 지시함수를 근사해낼 수 있다.

ReLU 네트워크가 여러 부분구조의 합으로 나타난다.

1. 지시함수의 유한 가중합

입력값 벡터 $x=(x_{1},\ldots,x_{n})$ 이 주어졌을 때, $f$가 르벡적분가능하므로 임의의 $\epsilon>0$ 에 대해 다음을 만족하는 $N>0$ 이 존재한다.

\[\int_{\cup_{i=1}^{n}\vert x_{i}\vert\geq N}\vert f\vert dx< \frac{\epsilon}{2}\]

다음을 정의하면,

\[E:=[-N,N]^{n}\] \[f_{1}(x) := \begin{cases} \max\lbrace f,0\rbrace & x\in E\\ 0& x\notin E \end{cases}\] \[f_{2}(x) := \begin{cases} \max\lbrace -f,0\rbrace & x\in E\\ 0& x\notin E \end{cases}\]

다음이 성립한다.

\[\int_{\mathbb{R}^{n}}\vert f-(f_{1}-f_{2})\vert dx< \frac{\epsilon}{2}\]

또한, 다음 두 집합을 정의하자.

\[\begin{align} V_{E}^{1} :&= \lbrace (x,y)\vert x\in E,0<y<f_{1}(x)\rbrace \\ V_{E}^{2} :&= \lbrace (x,y)\vert x\in E,0<y<f_{2}(x)\rbrace \end{align}\]

그러면 각 집합은 가측^measurable집합이므로, 각각 유한개의 $n+1$ 차원 큐브 $J_{j,i}$로 이루어진 르벡 덮개가 존재하여 다음을 만족한다.

\[\mu(V_{E}^{i}\;\triangle\bigcup_{j}J_{j,i})< \frac{\epsilon}{8}\tag{1}\]

또한, 각 큐브 $J_{j,i}$가 다음과 같은 형태로 주어진다고 가정하자.

\[J_{j,i}=[a_{1,j,i},a_{1,j,i}+b_{1,j,i}]\times\cdots\times[a_{n+1,j,i},a_{n+1,j,i}+b_{n+1,j,i}]\]

그러면, $J_{j,i}$는 $n+1$차원이므로, 다음과 같은 $n$차원 큐브 $X$들에 대한 지시함수에 대응된다.

\[X_{j,i}=[a_{1,j,i},a_{1,j,i}+b_{1,j,i}]\times\cdots\times[a_{n,j,i},a_{n,j,i}+b_{n,j,i}]\]

이때 각 지시함수를 다음과 같이 정의하자.

\[\phi_{j,i}(x) =\begin{cases} 1 & x\in X_{j,i} \\ 0 & x\notin X_{j,i} \end{cases}\]

그럼 식 (1) 로부터 다음이 성립한다. 여기서 $n_{i}$는 $J_{j,i}$ 들의 개수이다.

\[\int_{E}\vert f_{i}-\sum_{j=1}^{n_{i}}b_{n+1,j,i}\phi_{j,i}\vert dx< \frac{\epsilon}{8}\]

즉, 이로부터 임의의 르벡적분가능함수 $f$를 nonnegative한 함수 $f_{1},f_{2}$로 바꾸어 지시함수들의 유한합으로 근사할 수 있음을 확인했다.

2. ReLU Network

증명의 다음 과정은 ReLU network로 지시함수 $\phi_{j,i}$ 를 근사하는 것이다. 즉, 다음을 만족하는 함수 $\varphi_{j,i}$를 찾으면 된다.

\[\begin{align} \int_{X_{j,i}}\vert \phi_{j,i}-\varphi_{j,i}\vert dx &< \frac{\epsilon}{4(C+ \frac{3\epsilon}{4})}\int_{E}\vert \phi_{j,i}\vert dx \end{align}\]

즉, 임의의 $I\in\lbrace \phi_{j,i}\rbrace $ 와 $X=[a_{1},b_{1}]\times\cdots\times[a_{n},b_{n}]$ 에 대해

\[I=\begin{cases} 1 & x\in X \\ 0 & x\notin X \end{cases}\]

을 가정하면 네트워크 $\mathcal{N}$을 구성하여 이로부터 다음의 함수 $J$를 생성한다. $J$를 생성한다는 것은 네트워크를 하나의 함수로 보고 이를 $J(x)$ 꼴로 표기한다는 것이다.

\[\int_{E}\vert I-J\vert dx < \frac{\epsilon}{4C+3\epsilon}\prod_{i=1}^{n}(b_{i}-a_{i})\]

네트워크를 구성하는 방법은 복잡해서 여기서는 생략하겠으나, 핵심 아이디어는 함수를 잘게 나누어 함수의 지지집합^{support set}을 줄이는 것이다. 이때 잘게 나눈 함수를 얕은^shallow ReLU network로 나타내는데, 이를 Single ReLU Unit(SRU) 이라고 하며 다음을 만족한다.

임의의 $\delta>0, k=1,2,\ldots,n$ 에 대해 네트워크 $\mathcal{N}_{k}$ 는 다음 조건들을 만족한다. 여기서 함수 $R_{i,j,\mathcal{N}}$ 는 네트워크 $\mathcal{N}$에서 $i$번째 레이어의 $j$번째 노드에 ReLU 활성함수를 적용한 함수를 의미한다. $R_{0,\mathcal{N}}$는 입력 레이어를 의미한다.

$\mathcal{N}_{k}$ 의 각 레이어의 폭은 $n+4$이다.
$\mathcal{N}_{k}$의 깊이는 3이다.
$i=0,1,2,3, j=1,2,\ldots,n$ 에 대해 $R_{i,j,\mathcal{N}_{k}}=(x_{i}+N)^{+}$
$j=n+1,n+2$에 대해 $R_{i,j,\mathcal{N}_{k}}$ 과 관련된 가중치들은 모두 0이다.
첫번째 레이어(입력 레이어를 제외한)의 $n+3$번째 노드 $R_{1,n+3,\mathcal{N}_{k}}$ 는 다음을 만족한다.
- $0\leq R_{1,n+3,\mathcal{N}_{k}}(x)\leq 1, \quad \forall x$
- $R_{1,n+3,\mathcal{N}_{k}}(x)=0$ if
  \[(x_{1},\ldots,x_{k-1})\notin [a_{1},b_{1}]\times\cdots\times[a_{k-1},b_{k-1}]\]
- $R_{1,n+3,\mathcal{N}_{k}}(x)=1$ if
  \[(x_{1},\ldots,x_{k-1})\in [a_{1}+\delta(b_{1}-a_{1}),b_{1}-\delta(b_{1}-a_{1})]\times\cdots\times[a_{k-1}+\delta(b_{k-1}-a_{k-1}),b_{k-1}-\delta(b_{k-1}-a_{k-1})]\]
마지막 레이어의 $n+3$번째 노드 $R_{4,n+3,\mathcal{N}_{k}}$ 는 다음을 만족한다.
- $0\leq R_{4,n+3,\mathcal{N}_{k}}(x)\leq 1, \quad \forall x$
- $R_{4,n+3,\mathcal{N}_{k}}(x)=0$ if
  \[(x_{1},\ldots,x_{k-1})\notin [a_{1},b_{1}]\times\cdots\times[a_{k-1},b_{k-1}]\]
- $R_{4,n+3,\mathcal{N}_{k}}(x)=1$ if
  \[(x_{1},\ldots,x_{k-1})\in [a_{1}+\delta(b_{1}-a_{1}),b_{1}-\delta(b_{1}-a_{1})]\times\cdots\times[a_{k}+\delta(b_{k}-a_{k}),b_{k}-\delta(b_{k}-a_{k})]\]

즉, SRU에서는 각 레이어의 처음 $n+2$개 노드들은 output이 일정한 memory element인 반면, 나머지 두 노드는 computation element으로 기능한다.

References

Simon J.D. Prince, Understanding Deep Learning.
Lu et al., The Expressive Power of Neural Networks: A View from the Width