Divergence, Variational Autoencoder
본 포스트는 서울대학교 M2480.001200 인공지능을 위한 이론과 모델링 강의노트를 간단히 재구성한 것입니다.
Divergence
발산Divergence의 의미는 본래 미분기하학에서 정의되는데, 다양체 $M$에서의 두 점 $P,Q$와 좌표coordinates $\xi_{P},\xi_{Q}$ 에 대해 정의되고 다음을 만족하는 함수 $D(P:Q)$ 를 의미한다.
- $D(P:Q) \geq 0$.
- $D(P:Q)=0$ if and only if $P=Q$.
-
When $P,Q$ are sufficiently close, Taylor expansion of $D$ is written as
\[D(\xi_{P}:\xi_{P}+d\xi) = \frac{1}{2}\sum g_{ij}(\xi_{P})d\xi_{i}d\xi_{j}+o(\vert d\xi\vert^{3})\]
만일 다양체를 분포족으로 잡으면, 이는 두 확률분포 상의 거리metric와 유사한 개념이 된다. 유의할 것은 거리와는 다르게, 대칭성이 성립하지 않고 삼각부등식 역시 성립하지 않는다는 것이다. 대표적인 예시로는 Kullback-Leibler divergence가 있다.
Information
Information
사건 $x$에 대한 정보information는 불확실성을 의미한다고 보면 되는데, 이는 다음과 같이 역확률의 로그로 정의된다.
\[I(X) = -\log P(x) = \log \frac{1}{P(x)}\]Entropy
이와 유사하게, 이산형 확률변수 $X\sim P$ 에 대해서 엔트로피entropy는 다음과 같이 불확실성의 측도로 정의된다.
\[H(X) = \sum_{x}P(x) \log \frac{1}{P(x)} = \sum_{x}P(x)I(x) = \mathrm{E}[I(x)]\]엔트로피가 최대화되기 위해서는 확률분포 $P(x)$가 균등분포에 가까워야 한다.
엔트로피를 둘 이상의 확률변수에 정의하기 위해서 결합 엔트로피joint entropy를 다음과 같이 정의한다.
\[H(X,Y) = \sum_{x,y}P(x,y)\log \frac{1}{P(x,y)}\]이때 만일 $X,Y$ 가 독립이라면 $H(X,Y)= H(X)+H(Y)$ 가 성립한다. 또한, 조건부 확률분포에 대해서도 엔트로피를 정의할 수 있다. 이를 조건부 엔트로피conditional entropy라고 하며 다음과 같이 정의된다.
\[\begin{align} H(X\mid Y) &= \sum_{y}P(y)H(X\mid Y=y)\\ &= -\sum_{y}\sum_{x}P(x,y)\log P(x\mid y)\\ &= \mathrm{E}_{X,Y}\bigg[\log \frac{1}{P(x\mid y)}\bigg] \end{align}\]또한, joint entropy와 다음 관계가 성립한다.
\[H(X\mid Y)=H(X,Y)-H(Y)\]Mutual Information
변수들간의 공통된 정보의 정도를 파악하기 위한 측도로 상호정보mutual information이라는 개념이 존재한다. 이는 다음과 같이 정의된다.
\[\begin{align} I(X,Y):&= H(X)+H(Y)-H(X,Y)\\ &= \sum_{x,y}P(x,y)\log\frac{P(x,y)}{P(x)P(y)} \end{align}\]KL Divergence
두 확률분포 $P,Q$에 대한 KL 발산은 다음과 같이 정의된다.
\[\begin{align} KL(P:Q) &= \mathrm{E}_{P}\log \frac{1}{Q(x)}-\mathrm{E}_{P}\log \frac{1}{P(x)}\\ &= \sum_{x}P(X)\log\frac{P(x)}{Q(x)} \end{align}\]이로부터 상호정보를 결합확률분포와 주변확률분포의 곱 간의 KL 발산으로 재정의할 수 있다.
\[I(X,Y) = KL(P(x,y):P(x)P(y))\]즉, 내포된 의미를 생각한다면 독립으로부터의 거리정도를 생각할 수 있을 것이다.
Minimize KL Divergence
실제 분포가 $P$이고, 근사 분포가 $Q$일 때 아래의 두 최적화 문제는 서로 다른 해를 갖게 된다.
\[\min_Q KL(P:Q),\quad \min_Q KL(Q:P)\]Example Code
- Optimizer : Adam
- Loss : Monte Carlo approximated KL Divergence
-
True distribution $P$ : Gaussian Mixture (same weights)
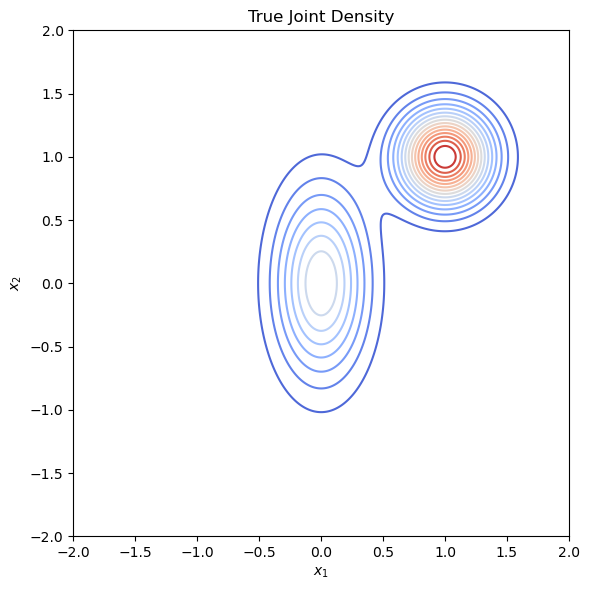
\[P =MVN\bigg(\begin{pmatrix}0 \\ 0\end{pmatrix}, \begin{pmatrix}0.25^{2}& 0 \\ 0&0.5^2\end{pmatrix}\bigg) + MVN\bigg(\begin{pmatrix}1 \\ 1\end{pmatrix}, \begin{pmatrix}0.25^{2}& 0 \\ 0&0.25^2\end{pmatrix}\bigg)\] - True distribution contour plot
- Optimization of $KL(P\Vert Q)$
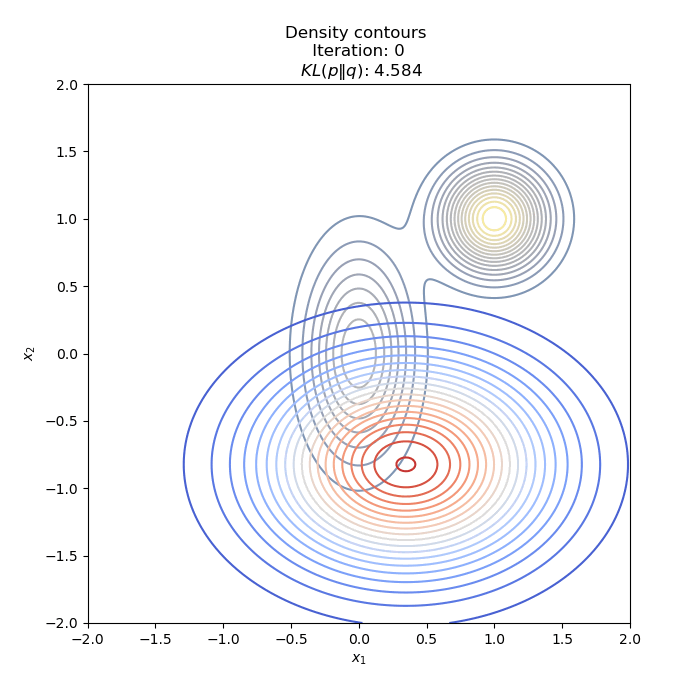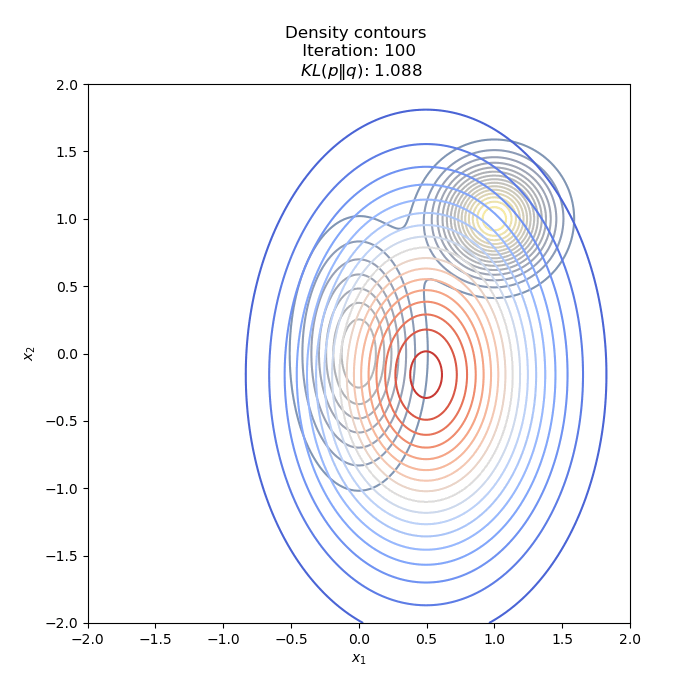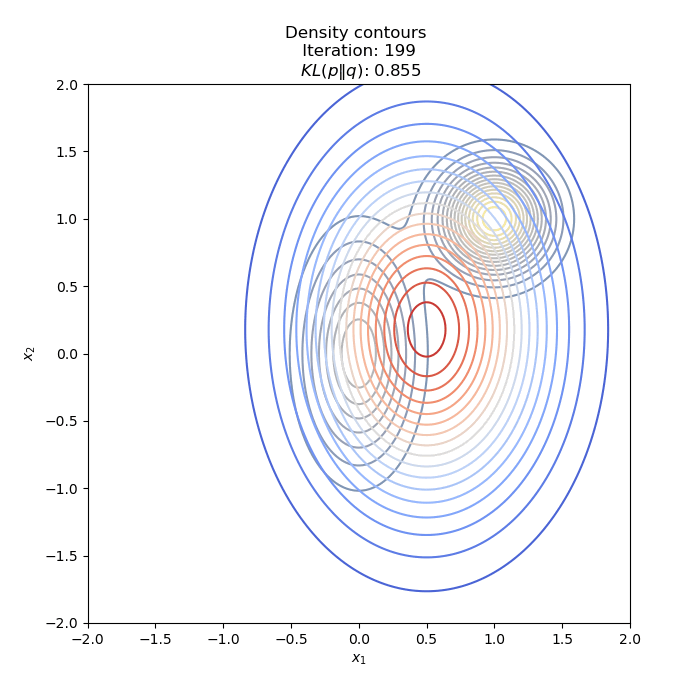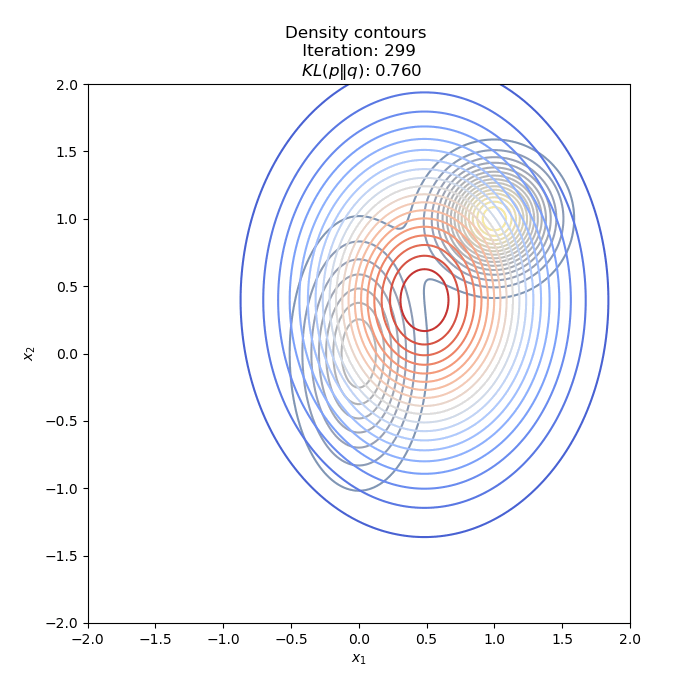
- Optimization of $KL(Q\Vert P)$ : two different Initial distribution
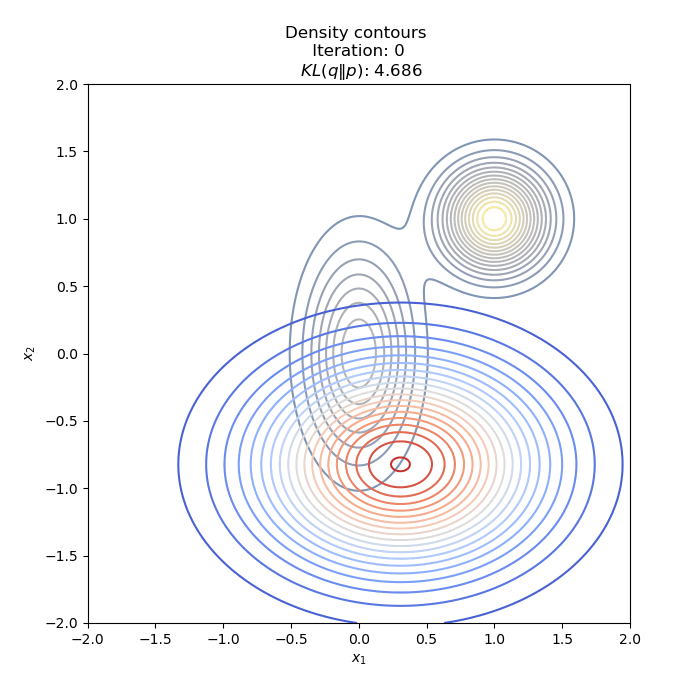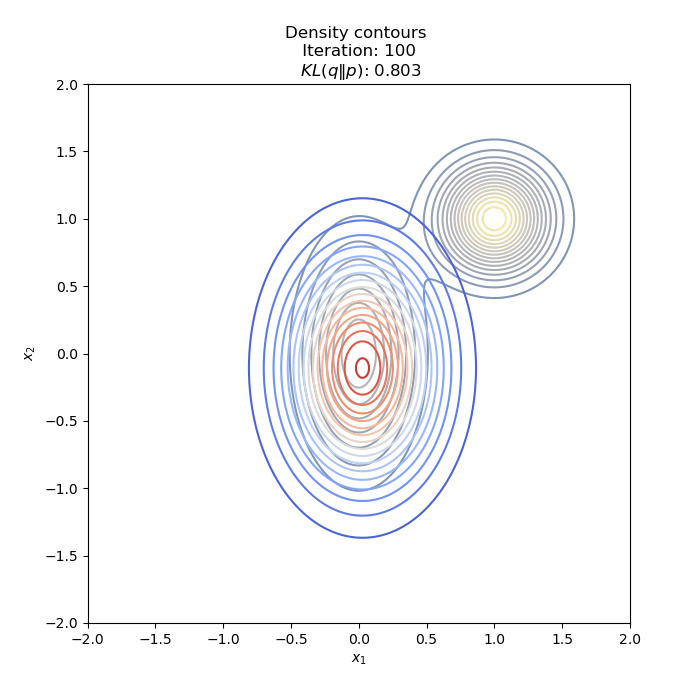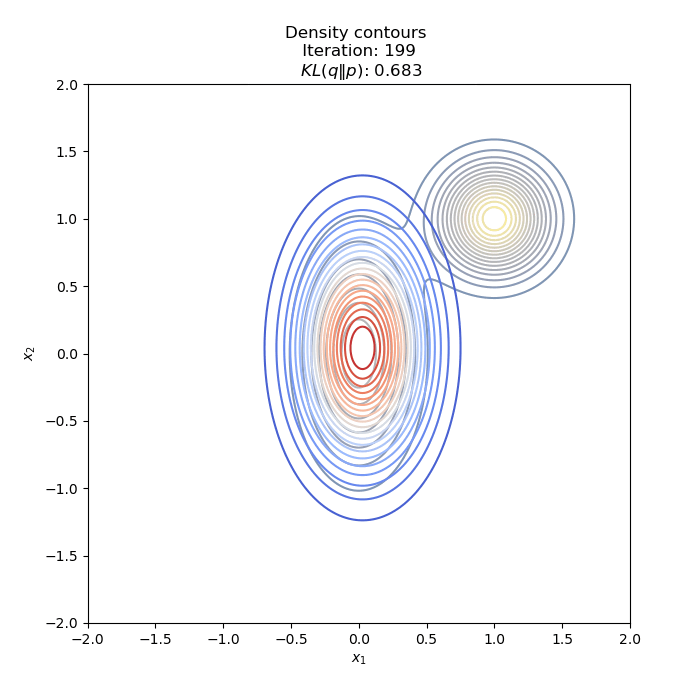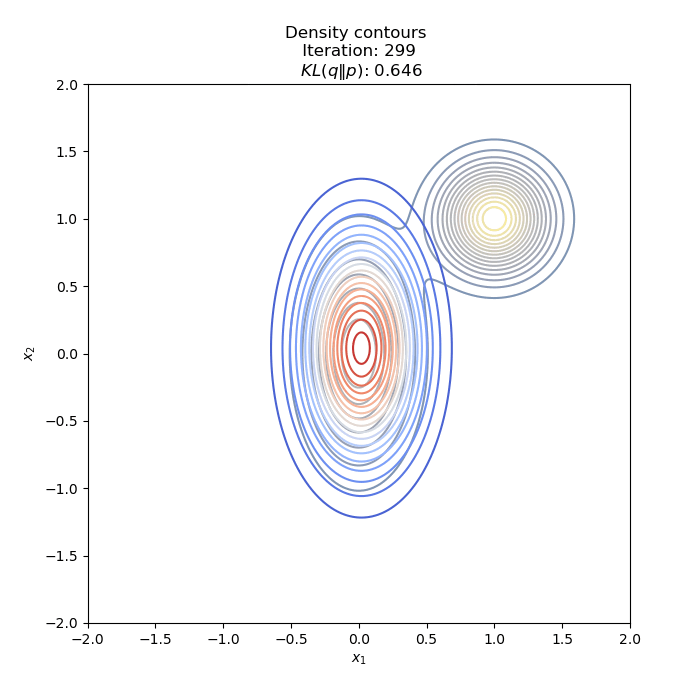
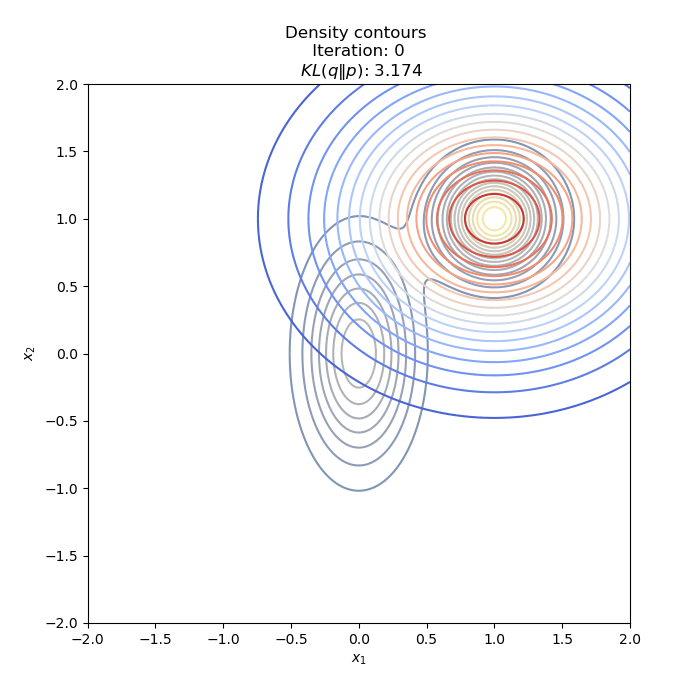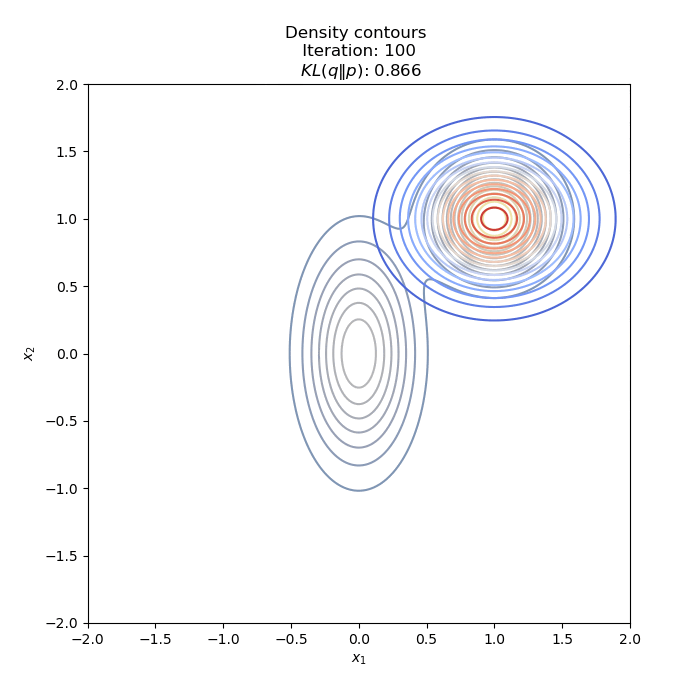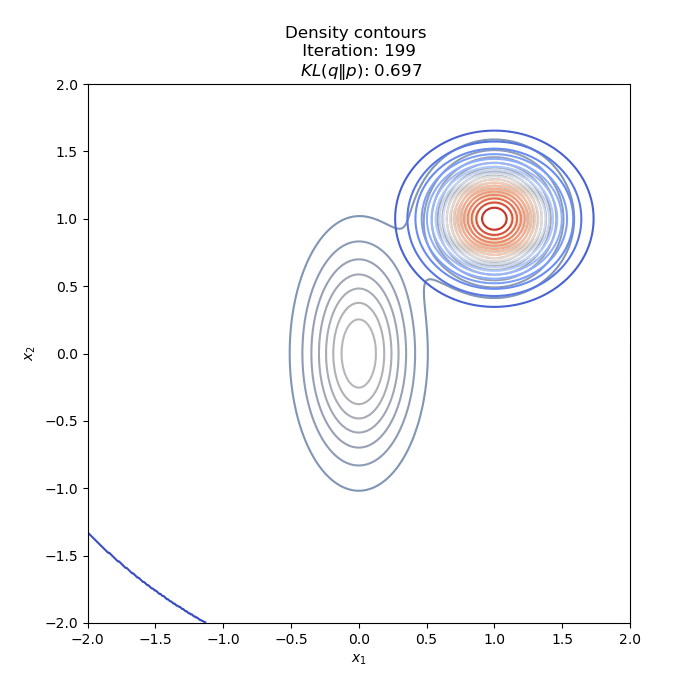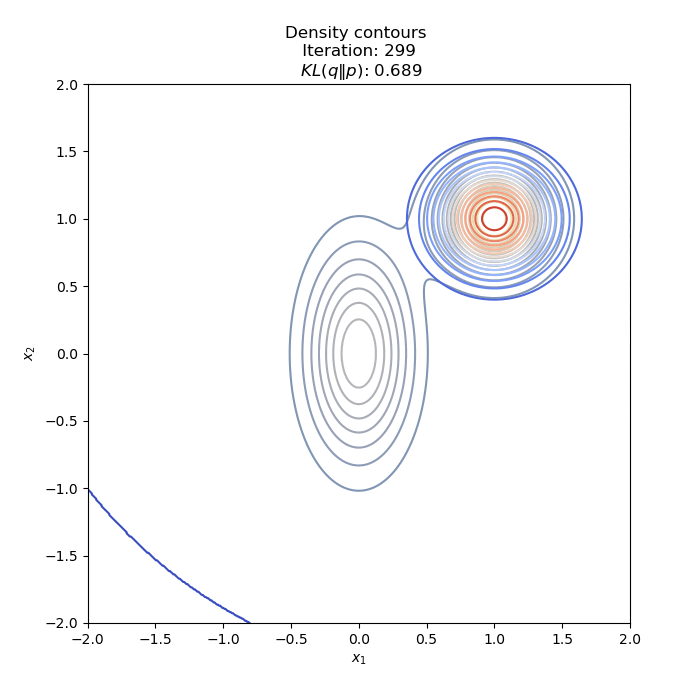
Full code on Github
Jensen-Shannon Divergence
KL 발산과는 달리, 대칭성을 가지고 있으며 유한한 값을 갖는다. KL발산의 경우 무한대로 발산하는 경우가 있어 최적화 과정에서 clip 함수를 취해주는 경우가 있는데(위 코드에서도 적용됨), JS 발산의 경우 0과 1사이의 값을 갖는다는 점에서 최적화에 적합하다고 볼 수 있다. 정의는 다음과 같다.
\[\begin{align} JSD(P\Vert Q) = \frac{1}{2}KL(P \Vert M) + \frac{1}{2}KL(Q\Vert M)\quad \text{where}\;M&= \frac{P+Q}{2} \end{align}\]- JSD는 대칭성을 갖는다.
- KL 계산의 로그 밑이 2인 경우, $0\leq JSD(P\Vert Q)\leq 1$ 가 성립한다.
Variational Methods
변분variational 추론이란, 다루기 어려운intractable 최적화 문제를 풀기 위해 목적함수를 근사하는 등 다양한 방법을 이용하는 것을 의미한다. 일반적으로 베이지안 통계에서 자주 사용되는데, 사후분포를 최대화하는 MAP 문제에서 사후분포를 다루기 쉬운 형태로 근사하는 방법(e.g. 라플라스 근사, 기댓값 전파)들이 사용된다.
Autoencoder
오토인코더Autoencoder는 데이터의 차원축소를 통해 잠재공간을 학습하기 위한 모델이다. 인코더와 디코더 두 부분으로 구성되며, 각각을 함수 $e,d$로 둘 때 최적화문제는 다음과 같이 주어진다.
\[\phi,\theta = \mathop{\arg\min}\limits_{\phi,\theta} \Vert X-(g_{\theta}\circ e_{\phi})(X)\Vert^{2}\]Variants
Denoising Autoencoder
일반적인 오토인코더는 과적합 가능성이 높다는 단점이 있다. 이를 해결하기 위해 노이즈를 추가한 입력 데이터를 제공하여 노이즈를 제거하는 오토인코더를 학습하게 되면 과적합의 가능성을 줄일 수 있다. 데이터 수가 적은 경우, 노이즈의 양(corruption level)을 크게 한다.
Sparse Autoencoder
Sparse autoencoder도 마찬가지로, 과적합을 피하기 위해 고안되었다. 이는 hidden unit activation을 통제하는데, hidden layer의 각 neuron이 동시에 활성화되는 비율을 일정 수준으로 제한한다. 일반적으로 5%의 비율을 사용한다.
Variational Autoencoder
VAE란, 잠재변수를 학습하는 대신 잠재변수의 분포를 가정하여 분포의 모수(ex. 정규분포의 평균, 분산)를 학습하는 것이다. 인코더에서는 잠재변수의 분포 $q(z\mid x)$ 를 학습하고, 디코더에서는 사후분포로부터의 샘플 $z\sim q$ 을 이용해 데이터를 재구성한다.
VAE의 손실함수는 다음과 같이 구성된다.
\[l(\theta,\phi) = -\mathrm{E}_{z\sim q_{\theta}(z\vert x_{i})}[\log p_{\phi}(x_{i}\vert z)] + KL(q_{\theta}(z\vert x_{i})\Vert p(z))\]여기서 $p(z)$ 는 잠재공간의 사전분포prior distribution이다. 손실함수의 첫번째 항을 reconstruction loss로 보고, 두번째 항은 regularization 항으로 생각할 수 있다. 일반적으로 잠재변수에는 정규사전분포를 이용한다. 위 손실함수의 부호를 바꾼 것을 ELBOEvidence Lower Bound Objective라고도 하는데, 이는 다음으로부터 유도된다.
ELBO
Evidence란, 입력 데이터들에 대한 로그가능도를 의미한다. 이때 로그가능도에 대한 하한을 아래와 같이 구할 수 있다.
\[\begin{align} \log p_{\phi}(x)&= \log\int p_{\phi}(x\vert z)p(z)dz\\ &= \log\int p_{\phi}(x\vert z)\cdot \frac{q_{\theta}(z\vert x)}{q_{\theta}(z\vert x)}\cdot p(z)dz\\ &= \log \mathrm{E}_{q}\bigg[\frac{p_{\phi}(x\vert z)p(z)}{q_{\theta}(z\vert x)}\bigg]\\ &\geq \mathrm{E}_{q}\log p_{\phi}(x\vert z)+ \mathrm{E}_{q}\bigg[\log \frac{p(z)}{q_{\theta}(z\vert x)}\bigg]\\ &= \mathrm{E}_{q}\log p_{\phi}(x\vert z) - KL(q_{\theta}\Vert p(z)) \end{align}\]여기서 세번째 부등식은 Jensen’s inequality로부터 성립한다. 즉, 로그가능도를 최대화하는 것이 목적이기 때문에 마지막 ELBO를 최대화하는 것이 성립한다.
Reparametrization Trick
역전파 과정에서 근사사후분포 $q_{\theta}$에 대한 직접적인 그래디언트 계산이 어렵다는 문제가 존재한다. 따라서 이를 해결하기 위해 다음과 같은 트릭을 이용한다.
\[q_{\theta}\sim N(\mu_{\theta},\sigma_{\theta}) \Rightarrow z=\sigma_{\theta}\xi+\mu_\theta,\;\;\xi\sim N(0,I)\]이를 이용하면 역전파 알고리즘을 사용할 수 있으며, 이로부터 딥러닝 모델로의 구현이 가능해진다.
References
- Shun ichi Amari - Information Geometry and its Applications
- Lecture Notes
- Code on Github
Leave a comment