Coordinate Ascent Variational Inference

Variational Inference

변분추론Variational Inference이란, 베이지안 추론의 근사적 방법론 중 하나입니다. 베이지안 추론에서 사후분포의 확률밀도함수는 다음과 같이 계산할 수 있습니다.

\[p_{Z|X}(z|x) = \frac{p_{X|Z}(x|z)p_Z(z)}{\int p_{X|Z}(x|v)p_Z(v)dv}\]

위 식에서, 특수한 경우가 아닌 이상 분모의 적분을 계산하는 것은 어렵습니다(intractable). 분모의 적분을 evidence라고도 합니다. 변분추론이란 사후분포를 다루기 쉬운 형태의 또 다른 분포 $q$로 근사하는 방법을 의미합니다. 이때, $q$는 근사하고자 하는 분포인 $p_{Z|X}$와의 Kullback- Leibler 발산을 최소화하는 방향으로 학습합니다.

\[D_{KL}(q_{Z|X}||p_{Z|X}) = \int q_{Z|X}(z|x) \log \frac{q_{Z|X}(z|x)}{p_{Z|X}(z|x)} dz\]

ELBO

위 식에서 확률변수 $X,Z$를 각각 관측가능한 데이터, 잠재변수(혹은 모수)라고 하면 로그가능도는 다음과 같이 분해됩니다.

\[\begin{aligned} \log p_{\phi}(x)&= \log\int p_{\phi}(x\vert z)p(z)dz\\ &= \log\int p_{\phi}(x\vert z)\cdot \frac{q_{\theta}(z\vert x)}{q_{\theta}(z\vert x)}\cdot p(z)dz\\ &= \log \mathrm{E}_{q}\bigg[\frac{p_{\phi}(x\vert z)p(z)}{q_{\theta}(z\vert x)}\bigg]\\ &\geq \mathrm{E}_{q}\log p_{\phi}(x\vert z)+ \mathrm{E}_{q}\bigg[\log \frac{p(z)}{q_{\theta}(z\vert x)}\bigg]\\ &= \mathrm{E}_{q}\log p_{\phi}(x\vert z) - KL(q_{\theta}\Vert p(z)) \end{aligned}\]

Evidence의 하한(Evidence Lower BOund)이라는 의미에서 ELBO라고 정의하며, 이를 최대화하는 학습 방향과 데이터의 로그가능도를 최대화하는 학습 방향이 일치함을 알 수 있습니다.

CAVI

변분추론에서 일반적인 사후분포의 근사 방식은, 모든 잠재변수들이 독립이라는 가정입니다. 즉 아래와 같습니다.

\[q(\mathbf{z}) = \prod_{j=1}^{K}q_{j}(z_{j})\]

이러한 근사를 mean-field approximation이라고도 합니다. 이를 이용하면, ELBO를 다음과 같이 정리할 수 있습니다.

\[\begin{align} \mathrm{ELBO} &= \mathrm{E}_{q}\log p_{\phi}(x|z) - KL(q_\theta(z)\Vert p(z))\\ &= \mathrm{E}_{q}\log p_{\phi}(x|z) - \mathrm{E}_{q}\log\frac{q_{\theta}(z)}{p(z)}\\ &= \mathrm{E}_{q}\log p_{\phi}(x,z) - \mathrm{E}_{q}\log q_{\theta}(z)\\ &= \int \prod_{j=1}^{K}q_{j}(z_{j})\log p_{\phi}(x,z)dz - \sum_{j=1}^{K}\mathrm{E}_{q}\log q_{j}(z_{j}) \end{align}\]

이때, $q_{2},\ldots q_{K}$에 대해서는 고정시키고, $q_{1}$에 대해서 ELBO를 최대화하는 문제를 풀고자 할 때 목적함수를 다음과 같이 나타낼 수 있습니다.

\[\begin{align} \mathcal{L}(q_{1}) &= \int q_{1}(z_{1}) \int q_{2}(z_{2})\cdots\int q_{K}(z_{K})\log(x,z_{1},\ldots,z_{K})dz_{K}\cdots dz_{1} - \mathrm{E}_{q}\log q_{1}(z_{1}) + \mathrm{const}\\ &= \int q_{1}(z_{1})\bigg( \mathrm{E}_{-1}\log p(x,z)\bigg)-\log q_{1}(z_{1})dz_{1} + \mathrm{const}\\ \end{align}\]

여기서 $\mathrm{E}_{-i}$ 은 $i$번째 잠재변수를 제외한 나머지 잠재변수들에 대한 기댓값을 의미합니다. 이는 로그확률의 기댓값으로 볼 수 있으므로 다음과 같이 unnormalized probability distribution

\[f_{i}(z_{i})\propto \exp\bigg(\mathrm{E}_{-i}\log p(x,z_{i},z_{-i})\bigg)\]

으로 나타낼 수 있습니다. 이를 이용하면, ELBO를 다시 아래와 같이 나타낼 수 있습니다.

\[\mathcal{L}(q_{1}) = -KL(q_{1}\Vert f_{1}) + \mathrm{const}\]

이를 최대화하기 위해서는, KL divergence 항이 0으로 수렴해야 하므로 $q_{1}=f_1$이 되어야 함을 알 수 있습니다. 이는 곧, $q_{1}$에 대한 업데이트가 $f_{1}$으로 이루어짐을 알 수 있습니다.

Special Case : Markov Chain

만일 잠재변수 간에 Bayes Net이 존재한다면, 앞서 언급한 $\mathrm{E}_{-i}$ 처럼 $i$번째 잠재변수를 제외한 나머지를 모두 사용할 필요가 없게 됩니다. 이는 $p(x,z)$ 가 factorized 될 수 있기 때문인데, 이로부터 기댓값을 계산할 때 Markov blanket만을 이용하면 됩니다. 즉, 아래와 같이 업데이트가 이루어집니다.

\[q_{j}(z_{j})\propto \exp\bigg(\mathrm{E}_{MB_{j}}\log p(x,z_{j},\mathbf{z}_{MB_{j}})\bigg)\]

Example. Gaussian Mixture

  • 예시를 통해 CAVI를 이해해보도록 하겠습니다.
  • 예시에서는 다음과 같은 $K$-Gaussian Mixture Model을 가정합니다.
\[\begin{aligned} \mu_j &\sim \mathcal{N}(0,1) \quad \text{for } j=1,\cdots,K\\ c_i &\sim \mathcal{U}(K) \quad \text{for } i=1,\cdots,N\\ x_i \vert c_i, \mu &\sim \mathcal{N}(c_i^T\mu,1) \quad \text{for } i=1,\cdots,N \end{aligned}\]
  • 이때, $c_i$는 $K$차원의 one-hot vector입니다.
  • CAVI를 사용하기 위해, 다음과 같이 모수 $\mu, c$를 잠재변수로 보고 mean-field 근사를 가정합니다.
\[q(\mu,c) = q(\mu\vert m, s^2)q(c\vert \phi) = \prod_{j=1}^{K}\mathcal{N}(\mu_j\vert m_j, s_j^2)\prod_{i=1}^{N}\mathrm{Multi}(1, \phi_i)\]
  • 여기서 $\phi_i$는 확률 $p(c_i=j)=\phi_{ij}$로 구성된 $K$차원 벡터입니다.
  • ELBO를 계산하면, 다음과 같습니다.
\[\begin{aligned} \mathrm{ELBO} &= \mathbb{E}_q\log p(x,z) - \mathbb{E}_q\log q(z)\\ &\propto \sum_j -\mathbb{E}_q\bigg[\frac{\mu_j}{2\sigma^2}\bigg] + \sum_i\sum_j \bigg[\mathbb{E}_q c_{ij} - \mathbb{E}_q\bigg[-\frac{(x_i-\mu_j)^2}{2}\bigg]\bigg] \\ &\;\;- \sum_i\sum_j \mathbb{E}_q\log\phi_{ij} + \sum_j \frac{1}{2}\log s_j^2 \end{aligned}\]
  • CAVI의 알고리즘을 적용하면, 각 잠재변수(모수)들에 대해 다음과 같이 업데이트를 진행합니다.

  1. $\phi_{ij}$

    \[\phi_{ij}^{new} \propto \exp\bigg(-\frac{1}{2}(m_j^2 + s_j^2) + x_i m_j\bigg)\]

  2. $m_j$

    \[m_j^{new} = \frac{\sum_i\phi_{ij}x_i}{1+\sum_i\phi_{ij}}\]

  3. $s_j^2$

    \[(s_j^2)^{new} = \frac{1}{1+\sum_i\phi_{ij}}\]

CAVI 알고리즘을 이용하여, 잠재변수의 학습이 이루어지는 과정을 살펴보도록 하겠습니다.

Python Implementation

패키지 불러오기

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib import animation
from IPython.display import HTML, Image

데이터 생성하기

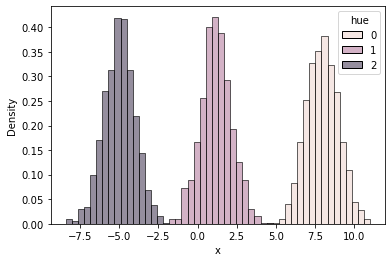
  • 여기서는 $K=3$으로 하고, 각 성분 분포에 대해 1000개의 데이터를 생성합니다.
  • mu_true에는 각 성분의 다음 모수가 저장됩니다.
\[\mu_1 = 8.0, \quad \mu_2 = 1.2, \quad \mu_3 = -5.0\]
  • 아래는 데이터를 생성하고, 각 성분을 구분하기 위해 색을 다르게 표시한 히스토그램입니다.
K = 3
mu_true = np.array([8.0, 1.2, -5.0])
n_sample = 1000

X = np.concatenate([np.random.normal(mu, 1.0, size=(n_sample, 1)) for mu in mu_true], axis=0).ravel()
hue = np.concatenate([np.full(n_sample, i) for i in range(K)], axis=0).ravel()
df = pd.DataFrame({"x": X, "hue": hue})

sns.histplot(data=df, x="x", hue="hue", stat="density", common_norm=False, bins=50)
plt.show()

png

CAVI 알고리즘을 적용하기 위해, 다음과 같이 CAVI 클래스를 정의합니다.

class CAVI(object):
    def __init__(self, X, K):
        self.X = X
        self.K = K
        self.N = X.shape[0]

    def initialize(self):
        self.phi = np.random.dirichlet([1.0] * self.K, size=self.N)
        self.m = np.random.randn(self.K)
        self.s2 = np.ones(self.K) * np.random.random(self.K)
        print(f"Initial m: {self.m}, s2: {self.s2}")

    def ELBO(self):
        t1 = np.log(self.s2) - self.m
        t1 = t1.sum()
        t2 = -0.5 * np.add.outer(self.X**2, self.s2 + self.m**2)
        t2 += np.outer(self.X, self.m)
        t2 -= np.log(self.phi)
        t2 *= self.phi
        t2 = t2.sum()

        return t1 + t2

    def update_phi(self):
        t1 = np.outer(self.X, self.m)
        t2 = -0.5 * self.m**2 - 0.5 * self.s2
        exp = t1 + t2[np.newaxis, :]
        self.phi = np.exp(exp)
        self.phi /= self.phi.sum(axis=1)[:, np.newaxis]

    def update_m(self):
        self.m = (self.phi*self.X[:, np.newaxis]).sum(0) * (1 + self.phi.sum(0))**(-1)
        assert self.m.size == self.K

    def update_s2(self):
        self.s2 =(1 + self.phi.sum(0)) ** (-1)
        assert self.s2.size == self.K
  • 학습을 진행하기 이전에, 만들어둔 CAVI 클래스의 인스턴스를 생성합니다.
  • initialize 메소드를 통해, 잠재변수의 초기값을 설정합니다.
np.random.seed(0)
cavi = CAVI(X, K)
cavi.initialize()


Initial m: [ 0.77529146  0.26491677 -0.45675722], s2: [0.06665737 0.9420893  0.1616041 ]

아래 코드는 학습 이전과 수렴 이후 모수에 대한 그래프를 그리기 위한 함수입니다.

def plot(ax, i, elbo):
    ax.clear()
    sns.histplot(data=df, x="x", hue="hue", stat="density", common_norm=False, bins=50, ax=ax, palette="Set2")
    bincount = np.bincount(cavi.phi.argmax(axis=1))

    samples = np.concatenate([
        np.random.normal(cavi.m[j], np.sqrt(cavi.s2[j]), size=(bincount[j], 1)) for j in range(K)
    ]).ravel()

    sns.kdeplot(samples, ax=ax, color="black", linewidth=1.5, label="q(x)")
    ax.set_title(f"Iteration {i} : ELBO = {elbo:.2f}")
    ax.legend()
    ax.set_xlim(-10, 10)
    ax.set_ylim(0, 0.5)
  • 학습은 다음과 같이 반복문을 적용하여 진행합니다.
  • 가장 최근의 ELBO 값을 저장하여, 업데이트 이후 ELBO와의 차이가 $10^{-6}$보다 작아지면 학습을 종료합니다.
last_elbo = -np.inf
fig, ax = plt.subplots(1, 2, figsize=(12, 4), sharey=True)

for i in range(100):
    if i == 0:
        plot(ax[0], i, cavi.ELBO()) # Initial plot

    cavi.update_phi()
    cavi.update_m()
    cavi.update_s2()

    elbo = cavi.ELBO()

    if elbo - last_elbo < 1e-6:
        break

    last_elbo = elbo

plot(ax[1], i+1, elbo) # Updated plot
plt.show()

png

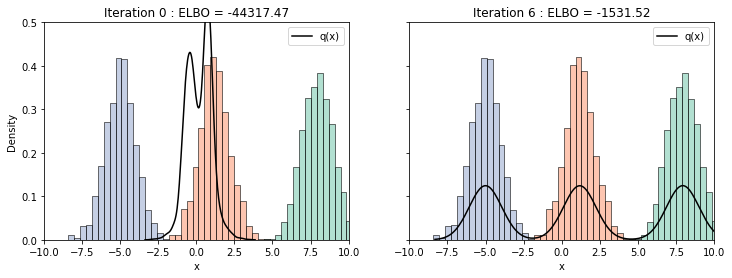
학습된 결과를 확인해보면, 비교적 적은 반복 횟수로도 초기 설정한 $\mu_1, \mu_2, \mu_3$에 빠르게 수렴하는 것을 확인할 수 있습니다.

References

  • Probabilistic Machine Learning, Advanced Topics
  • https://zhiyzuo.github.io/VI/

Leave a comment