Wasserstein GAN
Wasserstein GAN
이전 글에서에 GANGenerative Adversarial Network은 결과적으로 Jensen-Shannon divergence를 최소화하는 문제로 귀결되는 것을 확인했다. 이 경우 density ratio를 discriminator $D$로 추정하는 상황으로부터 도출되었는데, 이번에는 density ratio 대신 적분의 차이 형태로 주어지는 metric을 이용해보도록 하겠다. 이로부터 Wasserstein GAN을 도출할 수 있다.
Integral Probability Metrics
이전과 마찬가지로 $p^{\ast}$를 (알려져 있지 않은) 데이터의 실제 분포, $q_{\theta}$는 이를 모델링하는 분포로 생각하자. 그러면 두 밀도함수에 대한 Integral probability metricIPM은 다음과 같이 정의된다.
\[I_\mathcal{F} (p^{\ast}(x),q_{\theta}(x)) = \sup_{f\in\mathcal{F}} \left\vert \mathrm{E}_{p^{\ast}}f(x) - \mathrm{E}_{q_{\theta}}f(x)\right\vert\]또한, 위와 같이 정의된 IPM은 거리metric로 정의된다. 즉, non-negativity, symmetric, triangle inequality를 모두 만족한다. 이때 함수족 $\mathcal{F}$는 임의로 정해질 수는 없는데, 특정 함수족은 위 IPM이 거리조건을 만족하지 못하기 때문이다.
대표적으로 $\mathcal{F}$가 1-Lipschitz 함수들의 모임이면, 이때의 IPM은 Wasserstein distance가 된다. (Optimal Transport)
\[W_{1}(p^{\ast}(x),q_{\theta}(x)) = \sup_{f\in \Vert f\Vert_{Lip}\le 1} \mathrm{E}_{p^{\ast}}f(x)-\mathrm{E}_{q_{\theta}}f(x)\]다만, Wasserstein distance의 경우 위 정의의 상한을 구하는 것이 대부분의 경우에서 intractable하기 때문에, discriminator (혹은 critic) $D_{\phi}$를 이용하여 다음과 같이 변환한다.
\[\begin{align} W_{1}(p^{\ast}(x),q_{\theta}(x)) &= \sup_{f\in \Vert f\Vert_{Lip}\le 1} \mathrm{E}_{p^{\ast}}f(x)-\mathrm{E}_{q_{\theta}}f(x)\\ &\ge \max_{\phi:\Vert D_{\phi}\Vert_{Lip}\le 1} \mathrm{E}_{p^{\ast}}D_{\phi}(x)-\mathrm{E}_{q_{\theta}}D_{\phi}(x) \end{align}\]이때, 신경망 구조로 주어지는 $D_{\phi}$는 gradient penalty나 spectral normalization 등을 이용하여 Liptschitz 조건을 만족하도록 설정할 수 있다고 한다. 이는 아래에 자세히 다루도록 하겠다.
WGAN
GAN에서와 마찬가지로, 앞서 정의된 Wasserstein distance의 목적함수를 바탕으로 min-max optimization을 진행하면 이는 Wasserstein GAN이 된다. (Arjovsky et al., 2017)
\[\begin{align} \min_{\theta}W_{1}(p^{\ast}(x),q_{\theta}(x)) &\ge \min_\theta\max_{\phi:\Vert D_{\phi}\Vert_{Lip}\le 1} \mathrm{E}_{p^{\ast}}D_{\phi}(x)-\mathrm{E}_{q_{\theta}}D_{\phi}(x)\\ &= \min_\theta\max_{\phi:\Vert D_{\phi}\Vert_{Lip}\le 1} \mathrm{E}_{p^{\ast}}D_{\phi}(x)-\mathrm{E}_{q(z)}D_{\phi}(G_{\theta}(z)) \end{align}\]Density ratio estimation에서 일반적인 GAN은 두 밀도함수의 비를 discrimator로 추정하여 일종의 binary classification을 진행하였다. 반면, WGAN은 위 min-max optimization을 진행하지만 샘플이 $p^{\ast}$로부터의 것인지, $q_{\theta}$로부터의 것인지에 대한 분류를 진행하지는 않는다. 이로 인해 WGAN에서는 discriminator 대신 critic이라는 용어를 사용한다고 한다.
Improved Training of WGAN
Problem of weight clipping
Critic function $D_{\phi}$가 Liptschitz 조건을 만족하도록 하기 위해서 가장 간단하게는 weight clipping을 생각할 수 있을 것이다. 즉, $D_{\phi}$의 각 weight이 compact space $[-c,c]$에 속하도록 처리하는 것을 의미한다. 이를 통해 어떤 상수 $k$에 대해 critic이 $k$-Lipschitz 조건을 만족하도록 설정할 수 있다. 그러나 weight clipping을 사용할 경우 gradient vanishing, exploding의 문제가 발생한다.
이와 관련해 다음 정리와 보조정리가 성립한다. (Gulrajani et al., 2017)
Proposition
Compact metric space $\mathcal{X}$의 두 분포 \(P_{r},P_{g}\)를 가정하자. Wasserstein distance에서 정의되는 optimal critic을 $f^{\ast}$라고 정의하자. 또한, \(\Pi(P_{r},P_{g})\)를 이변량 분포들 중 marginal distribution이 각각 \(P_{r},P_{g}\)로 주어지는 분포들의 집합이라고 할 때, \(\pi=\arg\inf_{\pi\in\Pi(P_{r},P_{g})}\mathrm{E}_{(x,y)\sim \pi}\Vert x-y\Vert\) 를 정의하자 (optimal coupling). 이때, $f^{\ast}$가 미분가능하고 $\pi(x=y)=0$이며 $x_{t}=tx+(1-t)y$ 라고 할 때 ($0 \le t \le 1$) , 다음이 성립한다.
\[\Pr_{(x,y)\sim\pi } \left(\nabla f^{\ast}(x_{t}) = \frac{y-x_{t}}{\Vert y-x_{t}\Vert}\right) = 1.\]Corollary
\[\Vert \nabla f^{\ast}\Vert = 1 \quad \mathrm{a.e.}\quad \text{under }P_{r},P_{g}\]위 보조정리로부터 WGAN을 학습시키는 과정에서 optimal critic을 얻게 되면, 이것의 gradient norm이 almost surely $1$이 됨을 알 수 있다. 그러나, weight-clipping 제약조건을 사용하게 되면 $k$-Lipschitz 조건에 도달하기 위해 gradient norm을 $k$에 가깝도록 도출해내야 하고 이는 결국 매우 간단한extremely simple critic을 학습하는 결과를 초래한다.
Gradient Penalty
위 문제를 해결하기 위해 (Gulrajani et al., 2017)에서는 gradient penalty를 추가하는 방법을 제안했다. 목적함수는 다음과 같이 정의된다.
\[\mathcal{L} = \mathrm{E}_{q_{\theta}}D_{\phi}(x) - \mathrm{E}_{p^{\ast}}D_{\phi}(x) +\lambda \mathrm{E}_{\hat x \sim P_{\hat x}}\left[\left\Vert \nabla_{\hat x}D_{\phi}(\hat x)\right\Vert_{2}-1\right]^{2}\]여기서 $\hat x$는 random sample인데, \(P_{\hat x}\) 는 data distribution $p^{\ast}$과 generator distribution \(g_\theta\)에서의 샘플 쌍들을 잇는 직선을 따라 정의된다. 이는 위 proposition에서 그래디언트의 노음이 a.e. $1$임으로부터 구성된다.
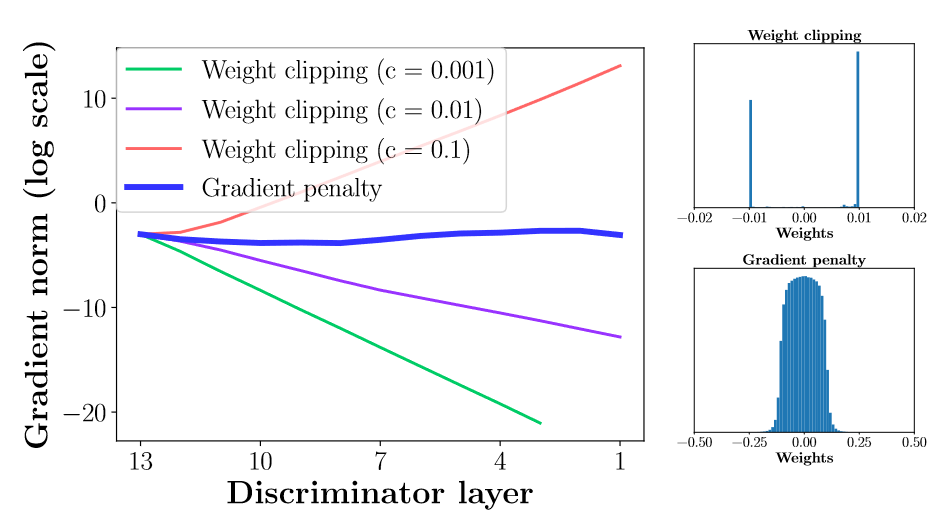 Gradient penalty vs Weight clipping
Gradient penalty vs Weight clipping
실제로 결과를 확인해보면, gradient penalty를 부여하는 방법에서 더 안정적인 그래디언트 학습이 진행됨을 확인할 수 있다.
References
- Arjovsky, M., Chintala, S., & Bottou, L. (2017). Wasserstein GAN (arXiv:1701.07875). arXiv. https://doi.org/10.48550/arXiv.1701.07875
- Murphy, K. P. (2023). Probabilistic machine learning: Advanced topics. The MIT Press.
- Xie, L., Lin, K., Wang, S., Wang, F., & Zhou, J. (2018). Differentially Private Generative Adversarial Network (arXiv:1802.06739). arXiv. https://doi.org/10.48550/arXiv.1802.06739
- Gulrajani, I., Ahmed, F., Arjovsky, M., Dumoulin, V., & Courville, A. (2017). Improved Training of Wasserstein GANs (arXiv:1704.00028). arXiv. https://doi.org/10.48550/arXiv.1704.00028
Leave a comment