AlexNet
AlexNet
이번 글에서는 “ImageNet Classification with Deep Convolutional Neural Networks”(2012) paper를 리뷰해보고자 한다. 이 논문은 2012년 ImageNet 대회에서 우승한 합성곱 신경망을 다루고 있다. 네트워크 이름은 대표저자 Alex Krizhevsky의 이름을 따 AlexNet이라고 부른다. 이전에 살펴본 LeNet-5와 구조는 비슷하지만, 신경망의 깊이와 사용된 기법들이 차이가 나는데, 이에 대해 다루어보도록 하겠다.
Architecture
AlexNet의 architecture는 아래 그림과 같다.
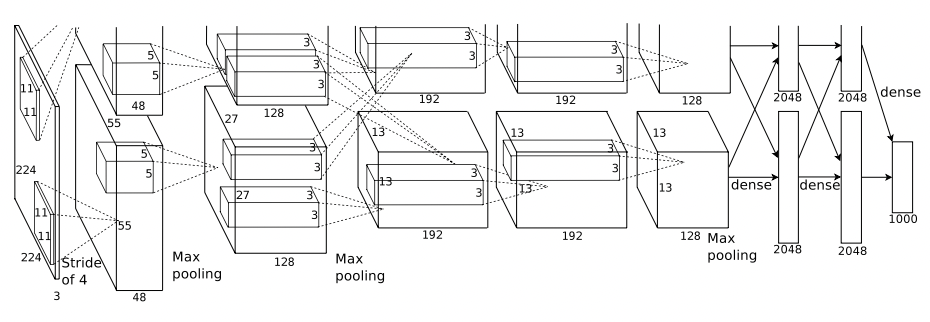 AlexNet architecture
AlexNet architecture
위 그림과 같이 AlexNet은 8개의 learnable layer들로 구성되어있는데, 이는 5개의 convolutional layer와 3개의 fully-connected layer(feedforward)로 구성되어 있다.
ReLU Nonlinearity
논문의 3.1절에서는 ReLU activation function을 다루고 있다. 최신 신경망 이론들에서는 대부분 ReLU 활성화 함수를 사용하는 것이 일반적이지만, 이 논문이 발표된 2012년 시점에서는 주로 하이퍼볼릭탄젠트(tanh)나 sigmoid 함수를 사용하는 것이 일반적이었다. 이 논문에서는 ReLU 활성화 함수를 사용하는 것이 효과적이라는 근거로, 4-layer convolutional neural net에서 CIFAR-10 이미지 데이터를 분류하는 문제를 구현한 뒤, ReLU와 hyperbolic tangent 활성화 함수를 각각 이용하는 네트워크를 설정해 training error rate를 비교했다. 여기서 ReLU 함수를 이용한 것이 오차율의 감소과정이 더 빠르게 일어났다. 즉, 신경망 자체의 학습(수렴)이 더 빠르게 일어났다(아래 그래프 참고).
Local Response Normalization
LRNLocal Response Normalization은 정규화 기법의 일종으로, 이 논문에서 가장 중요하게 보아야 할 기법이다. AlexNet은 두 개의 합성곱 레이어 위에 LRN이라는 경쟁적인 정규화normalization 레이어를 사용했다. 쉽게 설명하면, 가장 강하게 활성화된 뉴런이 다른 특성 맵에 있는 같은 위치의 뉴런을 억제한다는 것이다. 이 알고리즘은 아래 수식으로 표현된다.
\[b^i_{x,y}=a^i_{x,y}/\biggl(k+\alpha\sum_{j=\max(0,i-n/2)}^{\min(N-1,i+n/2)}(a_{x,y}^j)^2\biggr)^\beta\]위 식에서 $a_{x,y}^i$는 i번째 특성 맵의 $(x,y)$번째 neuron의 출력값을 ReLU function에 대입시킨 output value를 의미하고, $b_{x,y}^i$는 이에 대응하는 response-normalized activity이다. 위 식이 의미하는 것은, $a_{x,y}^i$ 값을 그대로 사용하는 것이 아니라, 인접한 $n$개의 특성 맵들의 $(x,y)$ 위치에 있는 값들을 제곱하여($a_{x,y}^j$), 이를 바탕으로 가중치를 부여해 normalize 한 $b^i_{x,y}$ 값을 사용한다는 것이다. 이러한 정규화 과정은 생물학적 뉴런에서도 관측되었으며, 각각의 특성 맵들을 서로 구분되게끔 하여 일반화 성능을 향상시킨다.
Tensorflow의 경우 tf.nn.local_response_normalization() 연산을 통해 구현할 수 있으며, keras layer에 추가하는 경우 Lambda 층으로 함수를 감싸서 사용하면 된다.
Overlapping Pooling
AlexNet의 다른 특징으로는 Pooling layer(CNN 참고)가 이전에 살펴본 것 처럼 Kernel size와 stride를 같게끔 하지 않고, stride를 kernel size보다 작게 만들어 중첩되는 pooling이 일어났도록 했다는 것이다. 이러한 방식을 통해 AlexNet은 top-1와 top-5 error rate를 0.4%, 0.3% 각각 감소시켰다고 한다.
Reducing Overfitting
Data Augmentation
AlexNet에서는 모델의 과적합을 피하기 위해 데이터를 인공적으로 증식하는 방법을 고안했다. 여기서는 기존 $256\times 256$ 픽셀 크기의 이미지를 각각 $224\times 224$ 크기의 부분 이미지로 추출하였고, 각 부분 이미지의 horizontal reflection까지 training sample에 포함시켜 총 $32\times32\times2=2048$ 배로 이미지 샘플을 키웠다.
또 다른 방법으로는 RGB channel의 강도를 조정하는 방법을 택했는데, 전체 training set의 RGB 픽셀값들로 PCA를 실행한 뒤, 각 이미지 데이터에 찾아낸 주성분들의 배수를 곱하는 방법을 사용했다. 즉, 각 RGB 이미지 픽셀값을 $I_{xy}=[I_{xy}^R,I_{xy}^G,I_{xy}^B]^\top$ 으로 두면 여기에 각각
\[[\mathbf{p_1,p_2,p_3}][\alpha_1\lambda_1,\alpha_2\lambda_2,\alpha_3\lambda_3]^\top\]의 값을 더하는 방법을 의미한다. 여기서 각 $\mathbf p$는 고유벡터를, $\lambda$는 이에 대응하는 고유값을 의미하며, 이 고유치는 각각의 $3\times3$ RGB covariance matrix에서 얻어진 것이다.
Dropout
Dropout 방식은 말그대로 네트워크의 진행과정에 있는 일부 노드의 값을 “버리는” 것이다. 즉, 어떤 layer에 대해 dropout을 한다는 것은 미리 설정된 dropout probability (ex. $p=0.5$) 의 비율에 해당하는 layer의 노드 출력값을 0으로 한다는 것이다. 다만, $p=0.5$이면 훈련때에 비해 테스트를 실행하는 과정에서 각 뉴런이 두 배 많은 입력 신호를 받게 된다(test에서는 dropout이 일어나지 않으므로). 따라서 훈련이 모두 끝난 뒤 각 입력의 연결 가중치에 keep probability보존 확률인 $(1-p)$ 만큼을 곱해주어야 하는데, 혹은 훈련하는 동안 각 뉴런의 출력을 keep probability로 나누는 방법도 있다. AlexNet에서는 처음 두 개의 fully-connected layer에 대해 dropout을 적용했으며, 이렇게 적용한 dropout은 모델의 과적합 문제를 해결하는데 매우 효과적인 도움을 준다.
References
- ImageNet Classification with Deep Convolutional Neural Networks, Alex. K et al.
- Hands on Machine Learning, 2e.
Leave a comment