Convolutional Neural Network

Convolutional Neural Network(이하 CNN)은 합성곱 신경망이라고 불리는데, 딥러닝의 여러 활용 분야 중 특히 computer vision 영역에서 주로 사용된다. Gradient-Based learning applied to Document Recognition 이라는 1998년 논문(링크)에서 손글씨 이미지를 인식하기 위해 LeNet-5 구조가 등장하였고, 여기서부터 합성곱 신경망이 본격적으로 연구되기 시작하였다.

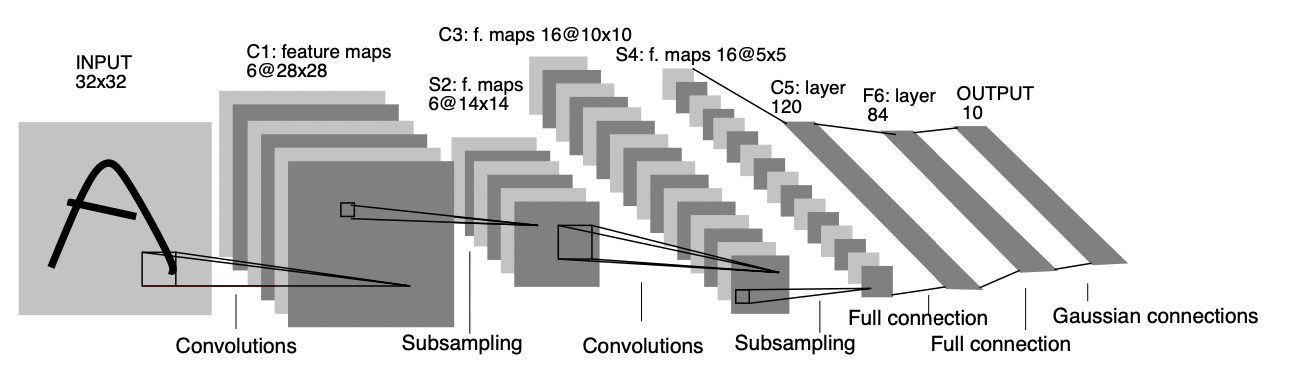스크린샷 2022-03-28 오전 11.16.15 (Architecture of LeNet-5)

위 그림은 LeNet-5의 구조를 설명하고 있는데, Convolution과 Subsampling이 일어나는 feature map이 두 개씩 존재한다. 이러한 layer들에서 어떤 연산이 일어나는지 살펴보도록 하자.

Convolutional Layer

LeNet-5의 Input layer는 $32\times32$ 픽셀의 이미지를 받고($W\times H$, 각각 width, height을 의미한다), 이를 처리하는 첫 번째 hidden layer는 6개의 plane으로 구성된 $28\times28$ feature map이라고 되어있다. 이 과정에서 합성곱 연산이 처리되는데, 각 $32\times32$ 이미지를 $5\times 5$ 크기의 Filter(convolutional kernel 라고도 한다)를 통과시켜 총 $28\times 28$ 크기의 feature map이 된다(아래 그림 참고, 여기서 레이어의 단면의 길이 3은 RGB 이미지인 경우와 같이 추가로 차원을 가지는 경우이고, 이를 채널channel이라고 한다!).

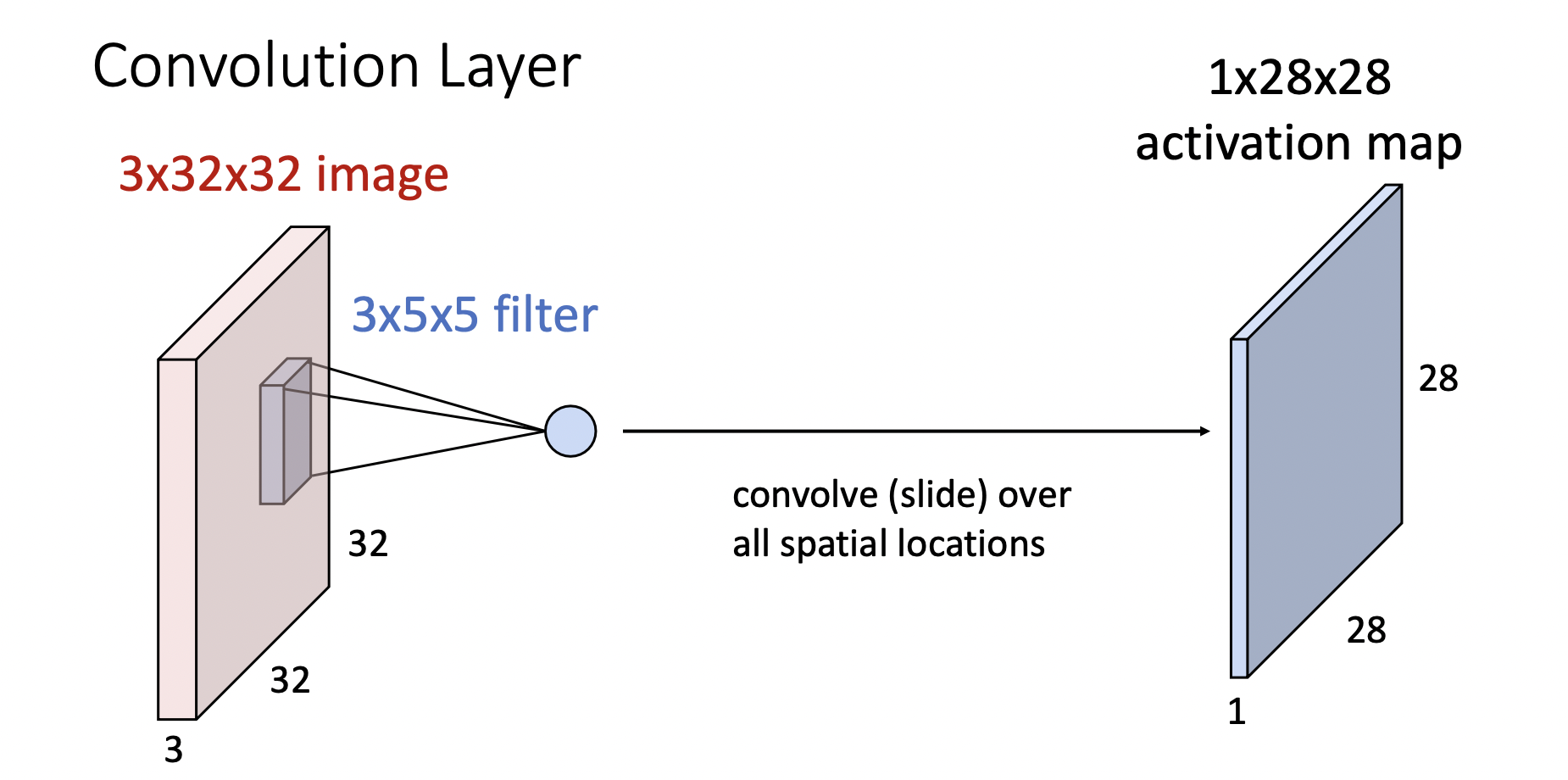
스크린샷 2022-03-28 오후 2.49.21

위처럼 크기가 $W\times W$ 이미지에 $F\times F$ 크기의 Filter를 적용하면 각 차원이 $W-F+1$ 개로 구성된 Feature map을 얻게 되고, 이러한 연산을 convolution이라고 한다. 역으로 생각하면, feature map의 각 원소는 원래 input layer의 어떤 영역(filter)에 대응되는데, 이 영역을 receptive field라고 한다. 또한, convolution 과정에서 Filter는 신경망의 노드와 마찬가지로 가중치 및 편향 텐서를 처리한다. 따라서 서로 다른 텐서들을 가진 Filter들을 처리하면 한 convolutional layer에 여러 feature map을 얻을 수 있고, 앞서 살펴본 LeNet-5의 경우 첫째 hidden layer가 6개의 Filter을 이용해 얻은 $6@28\times28$ convolutional layer이다.

그런데 위 LeNet-5의 convolutional layer처럼 일반적으로 크기가 1보다 큰 Filter을 취하면 당연히 초기 이미지보다 크기가 감소하게 된다. 따라서 이를 방지하기 위해 입력값 주위로 0의 값을 갖는 데이터들을 추가하는데, 이를 zero padding 이라고 한다. 일반적으로 padding의 크기를 $(F-1)/2$ 로 두어($F$ : 필터 크기) Input과 Output이 동일하도록 한다.

Pooling Layer

LeNet-5의 두번째 hidden layer는 Subsampling Layer인데, 이를 Pooling layer라고도 한다. 일단 convolutional layer을 통해 데이터의 부분별 특성을 대략적으로 파악한 후에는 더이상 receptive field의 구체적인 위치에 집착할 필요가 없어진다. 따라서 모델의 성능 향상에 초점을 두고 데이터를 축소시키는 데 Poolingsubsampling 연산을 사용한다. 이는 원 데이터를 작은 사이즈의 데이터로 줄이는 과정이다. 물론 앞서 언급한 합성곱 연산으로도 데이터 사이즈의 축소가 가능하지만 효과적인 축소가 일어나지는 않기에 별도의 pooling layer을 두는 것이다. Pooling에는 max pooling, average pooling, stochastic pooling 등 여러 종류가 존재하지만, 공통적으로 수행하는 연산은 input data를 여러 구역으로 나눈 뒤 해당 구역에서 조건을 만족하는 값만을 추출하고 나머지 데이터를 버리는 과정이다.

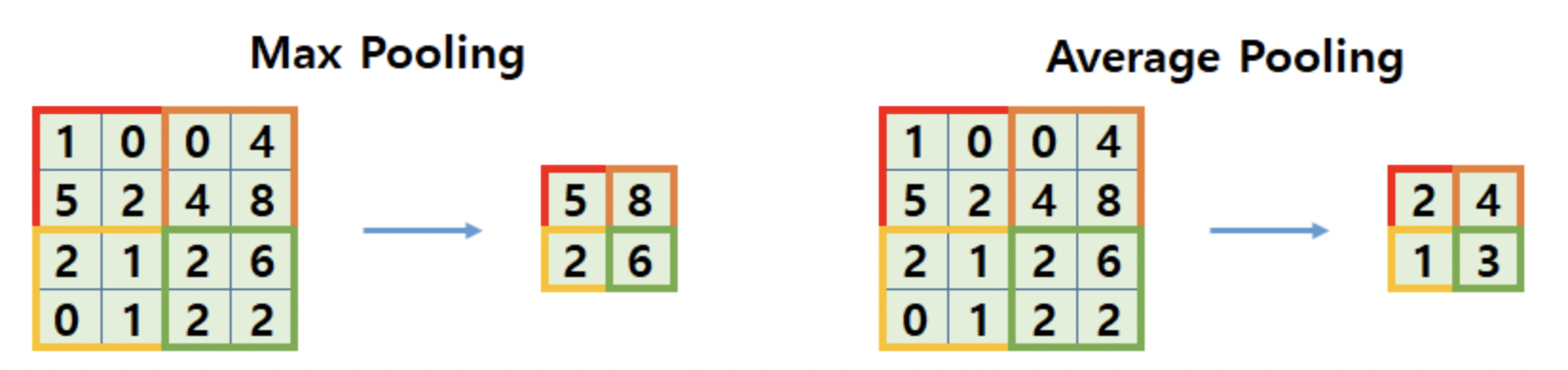
스크린샷 2022-03-28 오후 3.37.47

대표적으로 Max pooling과 Average pooling을 살펴보도록 하자(위 그림). Max pooling의 경우 각 구역에서 최댓값(max)를 추출하고, average pooling은 각 구역 데이터들의 평균값을 추출한다. 이 과정에서 모두 $4\times4$ 크기의 Input data가 $2\times2$의 데이터로 처리된 것을 확인할 수 있다. 데이터의 크기가 줄기 때문에, 모델의 학습 과정에서 추정해야 할 Parameter의 크기가 줄고, 이로 인해 모델의 과적합을 억제할 수 있는 효과가 있다. 다만, pooling을 잘못 이용할 경우 input data의 변화를 캐치해낼 수 없게 될 가능성이 있다.

LeNet-5의 경우 이전 convolutional layer의 6가지 feature map 각각을 $2\times2$ 영역들로 처리하고, average pooling으로 subsampling이 이루어진다. 이후 다시 convolution-subsampling의 과정을 또한번 거쳐 첫번째 과정에서는 데이터의 큰 부분의 특성을, 다음 과정에서는 좀 더 세부적인 부분의 특성을 파악하는 것으로 생각하면 된다.

일반적으로는, Max pooling이 Average pooling보다 성능이 더 좋아서 대부분의 CNN 구축에 max pooling을 사용한다. 그러나 평균을 계산하는 것이 최댓값을 계산하는 것 보다 통계적으로 정보손실이 적기 때문에, 이전 레이어의 데이터를 조금 더 보존하고 싶다면 average pooling을 사용하면 된다. 최근 신경망 구조에서는 global average pooling layer전역평균풀링 도 등장하는데, 이는 각 특성 맵에 커널을 적용하는 것이 아니라 각 특성 맵에 속한 전체 데이터의 평균을 구하는 것이다. 이 과정에서 특성맵 데이터들의 정보가 전부 사라지지만, 출력층에서는 유의미하게 사용된다.

CNN Structure

LeNet-5에서 살펴본 것과 마찬가지로, 일반적으로 CNN은 “Input-Convolution-Pooling-Convolution-Pooling-fully connected-Output” 의 형태를 갖는다. 여기서 fully connected 부분은 feedforward network를 의미한다. 이때 합성곱 커널을 설정하는 과정에서 필터의 크기를 너무 크게 설정하지 않는 것이 중요한데, 오히려 큰 필터 하나 대신 작은 필터로 여러번 연산을 수행하는 것이 효과적이다. 예로 $5\times 5$ 필터는 26개의 parameter를 추정해야 하지만, $3\times 3$ 필터 두번은 $18+2=20$개의 parameter를 추정하므로 더 효과적이다.

CNN with Tensorflow

이전에 MNIST 손글씨 데이터로 Simple feedforward network를 구현하였는데, 이번에는 앞서 살펴본 convolution, pooling 등의 개념을 직접 구현해보도록 하자. 이러한 CNN 관련 레이어들은 keras에서 제공하고 있으며, 여기서는 MNIST 데이터를 LeNet-5를 이용해 처리해보도록 하자.

import tensorflow as tf
import numpy as np
from tensorflow import keras
from keras.utils.np_utils import to_categorical

(X_train, y_train), (X_test, y_test) = keras.datasets.mnist.load_data()

이전과 마찬가지로 MNIST 데이터셋을 위와 같이 로드하였다. 이를 바탕으로 다음과 같이 CNN을 구성하면 된다. 우선 LeNet-5의 레이어 구성을 다시한번 살펴보면 다음과 같다.

Layer Type Feature Map Size Kernel Size Stride Activation
Input 1 32*32 - - -
Conv 6 28*28 5*5 1 tanh
Average Pooling 6 14*14 2*2 2 -
Conv 16 10*10 5*5 1 tanh
Average Pooling 16 5×5 2×2 2 –
Fully Connected – 120 – – tanh
Fully Connected – 84 – – tanh
Fully Connected – 10 – – softmax

위 레이어 구성처럼 Input layer를 제외하고 7개의 레이어로 구성되어 있는데, keras의 keras.models.Sequential을 이용하면 레이어를 가시적으로 쉽게 쌓고, 모델을 컴파일할 수 있다. 그전에, 일반적으로 Convolutional layer에 데이터를 처리하기 위해서는 앞서 살펴본 channel의 차원을 별도의 축으로 지정해줘야 한다. 즉, MNIST의 경우 각 데이터의 shape이 (28, 28) 로 출력되는데(X_train[0].shape), 이를 (28, 28, 1)이 출력되도록 만들어야 한다는 것이다. 이를 위해서 numpy의 np.newaxis를 이용하면 된다.

# Adding new axis
X_train = X_train[:,:,:, np.newaxis]
X_test = X_test[:,:,:, np.newaxis]
X_train[0].shape

이후, 이전에 feedforward network를 구성할 때와 마찬가지로 one-hot encoding과 데이터 정규화를 진행하면 된다.

# One-hot encoding
num_classes = 10
y_train = to_categorical(y_train, num_classes)
y_test = to_categorical(y_test, num_classes)
# Data Normalization
X_train = X_train.astype('float32')/255
X_test = X_test.astype('float32')/255
X_test = X_test.astype('float32')/255

이제 본격적으로 LeNet-5를 구성해보자.

# LeNet-5
class Lenet(Sequential):
    def __init__(self, input_shape, nb_classes):
        super().__init__() # Sequential class의 __init__ 상속
        
        self.add(keras.layers.Conv2D(
            6, kernel_size=(5,5), strides=(1,1), activation = 'tanh', input_shape=input_shape, padding = "same"
        ))
        
        self.add(keras.layers.AveragePooling2D(
            pool_size = (2,2), strides = (2,2), padding = "valid"
        ))

        self.add(keras.layers.Conv2D(
            16, kernel_size = (5,5), strides = (1,1), activation='tanh', padding='valid'
        ))

        self.add(keras.layers.AveragePooling2D(
            pool_size = (2,2), strides = (2,2), padding='valid'
        ))

        self.add(keras.layers.Flatten())
        self.add(keras.layers.Dense(120, activation='tanh'))
        self.add(keras.layers.Dense(84, activation='tanh'))
        self.add(keras.layers.Dense(nb_classes, activation='softmax'))

        self.compile(
            optimizer='adam', loss='categorical_crossentropy', metrics = ['accuracy']
        )

굳이 class를 만들지 않고 keras.models.Sequential()안에 레이어들을 리스트로 나열해 모델을 컴파일하는 방법도 있긴 하다. 우선 코드를 살펴보면, 위 Lenet 클래스는 keras의 Sequential 클래스를 상속받아서 작동한다. 이때 super().__init__ 은 부모클래스인 Sequential 클래스의 __init__ 메소드를 LeNet의 __init__ 메소드에 사용(참조)한다는 것을 의미한다. 이후 self.add() 들로 이어지는 코드들은 각각 레이어를 순서대로 쌓는 과정을 의미한다.

keras.layers.Conv2D는 2차원 convolutional layer을 의미한다. kernel_size는 Filter의 크기를 의미하고, strides는 보폭이라는 의미처럼 filter 연산 사이를 몇칸 띄고 처리할 것인지 의미한다. 즉, strides와 kernel_size가 동일하면 Pooling layer가 된다는 것을 알 수 있다. 마지막으로 Padding 은 valid, same의 두 값을 취하는데, 각각 padding을 설정하지 않는 것과 데이터 크기변화가 없도록 padding을 설정하는 것을 의미한다.

이후 Dense(feedforward) layer들을 추가하기 위해 먼저 합성곱 레이어들을 처리한 출력값을 1차원 벡터로 변경하는 flatten layer을 추가한 후 dense layer들을 연결했다(이전 simple neural network 참고). 최종적으로 model.compile을 통해(keras.models.Sequential의 메소드이다) 최적화는 Adam 알고리즘으로, 손실함수는 cross-entropy를 이용하도록 했다. 모델의 성능을 파악하는 metric은 정확도(accuracy)로 설정했다. 마지막으로 다음과 같이 필요한 파라미터들을 입력하면 모델이 완성되고, summary() 메소드를 이용하면 모델의 구성을 한눈에 확인할 수 있는 출력결과(아래 그림 참고)를 얻을 수 있다. 여기서는 총 학습해야 할 parameter의 개수와 레이어별 parameter의 개수 등을 확인할 수 있다.

model = Lenet(X_train[0].shape, num_classes)
model.summary()

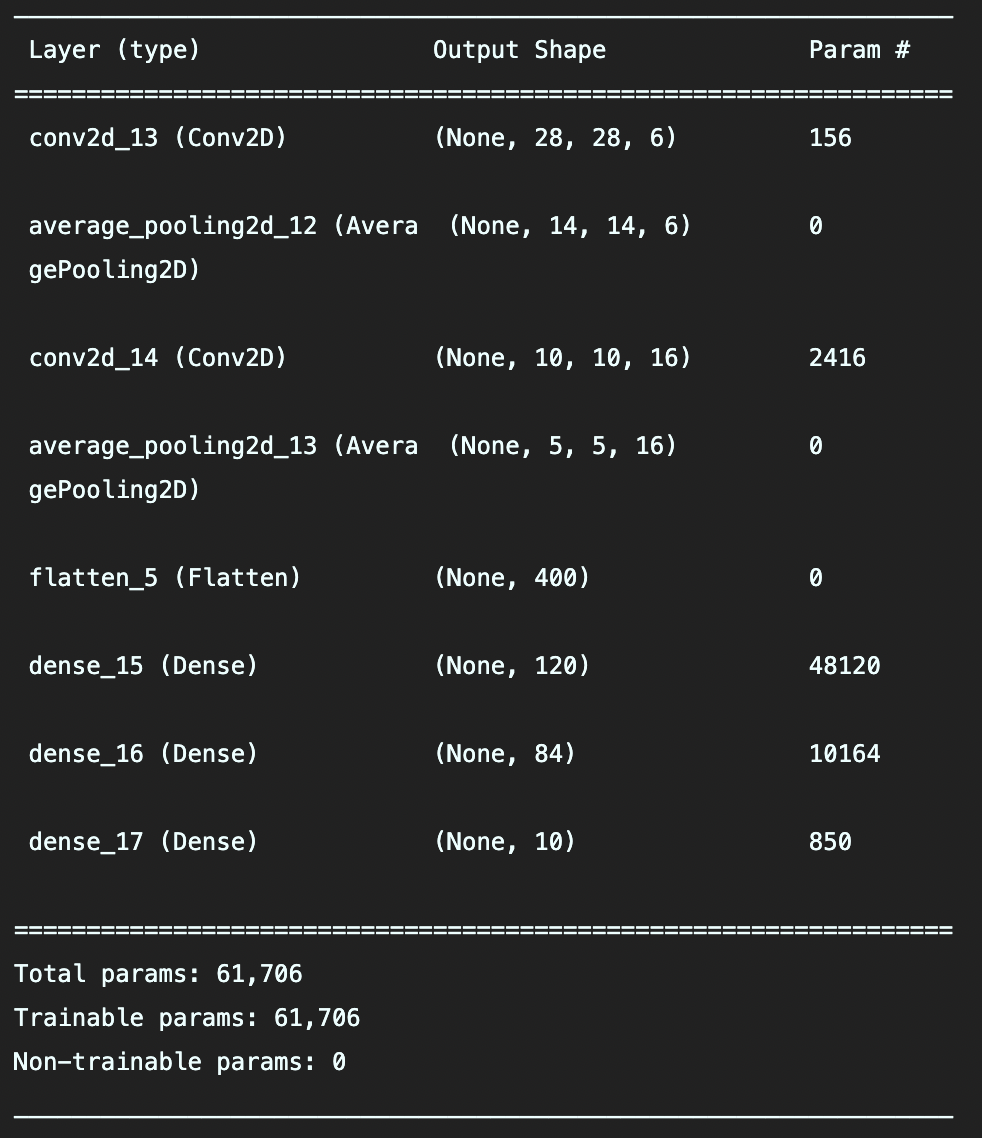
스크린샷 2022-03-30 오후 1.22.58

모델을 훈련하는 과정에서 tensorboard를 이용하면 모델의 metrics에 대한 plot을 확인하거나, 모델 훈련과정의 로그를 쉽게 저장하여 확인할 수 있다(공식문서 참조). 이는 다음과 같이 log directory를 만들어 설정할 수 있다.

# logging
import datetime
log_dir = "logs_cnn/fit/"+ datetime.datetime.now().strftime('%Y%m%d-%H%M%S')
tensorboard_callback = tf.keras.callbacks.TensorBoard(log_dir = log_dir, histogram_freq=1)

추가로, 모델을 훈련시키는 과정에서 진행상황을 알 수 있도록 progress bar를 생성하는 addon이 있는데, 다음과 같이 불러와서 사용할 수 있다.

import tensorflow_addons as tfa
tqdm_callback = tfa.callbacks.TQDMProgressBar()

이를 바탕으로 다음과 같이 모델을 훈련시키면 되는데, callbacks는 모델을 훈련 및 예측하는 메서드에서 중간과정을 처리하는 메서드로, 여기서는 앞서 정의한 tensorboard와 tqdm을 리스트 형태로 대입하면 된다. 훈련 시간은 epoch 하나당 40초가량 소요되었고, validation accuracy는 98.71%가 나왔다.

model.fit(
    X_train, y_train, epochs=10, validation_data=(X_test, y_test),
    callbacks=[tensorboard_callback, tqdm_callback],
    verbose=0, use_multiprocessing = True
)

이제 모델의 훈련 과정을 저장된 tensorboard log를 통해 확인해보자. 터미널을 통해 사용중인 conda environment를 activate하고, 작업중인 경로에서 tensorboard --logdir logs_cnn/fit를 입력하면 localhost:XXXX 형태로 로컬환경에서 텐서보드가 실행됨을 알려준다. 이를 브라우저로 접속하면

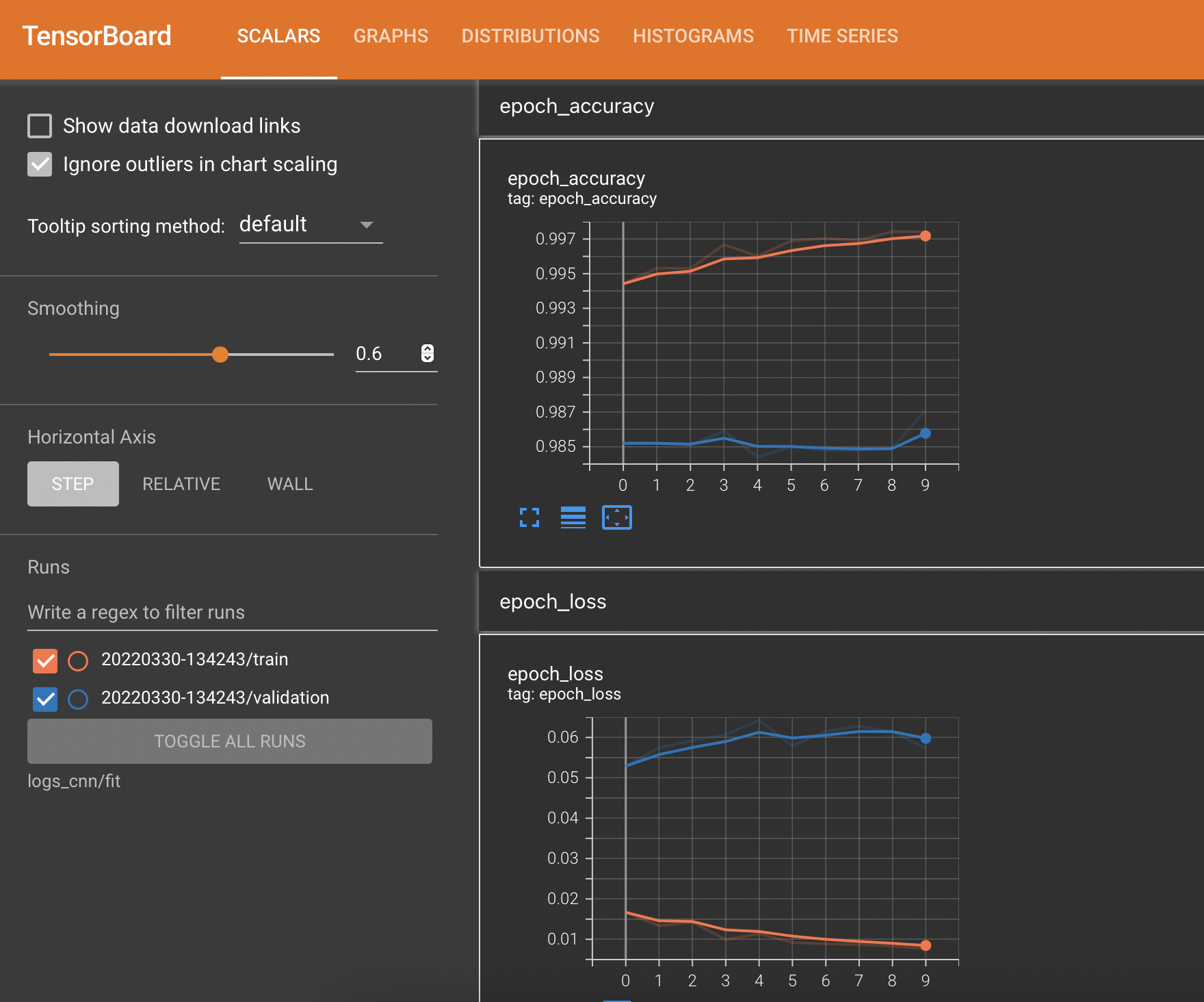
스크린샷 2022-03-30 오후 2.08.35

스크린샷처럼 train data와 validation data(여기서는 X_test, y_test)에 대한 epoch별 loss, metrics 곡선을 얻을 수 있다. Validation accuracy 98% 이상이 도출되었고 모델이 꽤 좋은 성능을 낸다는 것을 알 수 있다.

References

  • Gradient-based learning applied to document recognition, Yann LeCun et al. 1998.
  • Hands on Machine Learning. 2e.
  • Lecture note of “Deep Learning for Compuer Vision”, UMich EECS
  • https://datahacker.rs/lenet-5-implementation-tensorflow-2-0/

Leave a comment