LSTM-FCN
LSTM Fully Convolutional Networks for Time Series Classification
최근 공모전 준비로(추후에 마무리 후 포스팅 예정) Time Series Classification 기법들에 대해 알아보면서, 딥러닝(RNN, CNN) 기반의 방법중 하나인 LSTM-FCN을 알게 되었다. RNN의 개념부터 LSTM-FCN으로 시계열을 처리하는 네트워크까지 차근차근 개념을 다루어보도록 하겠다.
RNN
RNN은 시계열과 같이 순차적인 입력값을 갖는 벡터/행렬들을 처리하기 위해 고안된 네트워크이다. 다음과 같은 가장 단순한 형태인 한개의 레이어(A)를 갖는 RNN을 살펴보자.
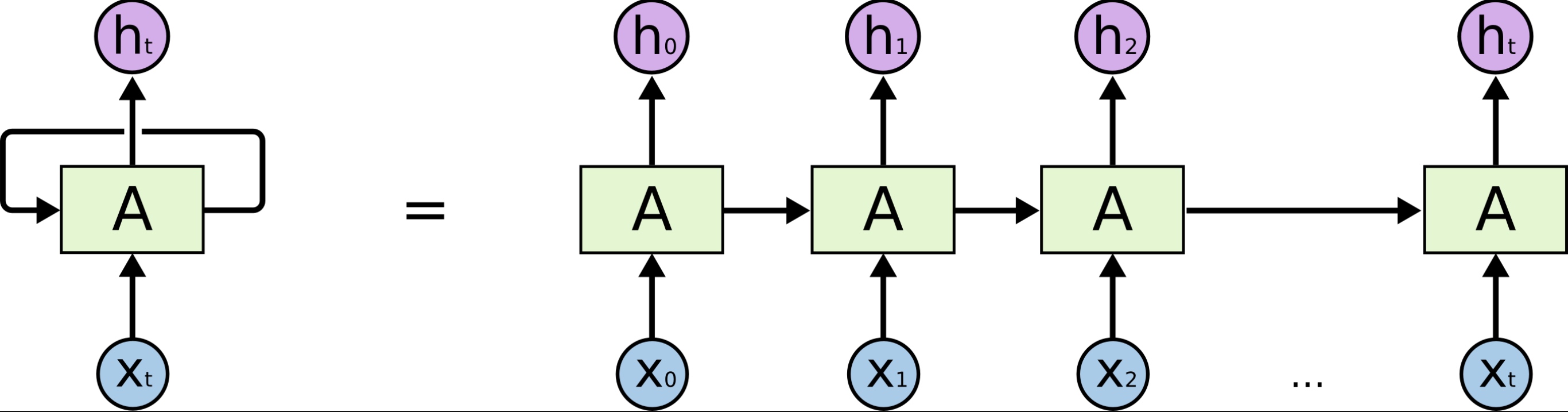(Image from https://towardsdatascience.com/introduction-to-recurrent-neural-network-27202c3945f3)
RNN의 순환레이어 A는 각 time step $t$의 출력값 $y_t$(위 그림의 $h$에 대응됨)를 처리하기위해 해당 time step의 입력값 $x_t$와 더불어 이전 time step의 출력값 $y_{t-1}$을 이용한다. 즉,
으로 나타내지는데, 이때 행렬 $\mathbf W_x, \mathbf W_y$는 각각 입력($x$)에 대응하는 행렬, 이전출력 $y$에 대응하는 행렬이다. 또한, 함수 $\phi$는 활성화함수를, $\bf b$는 편향벡터를 의미한다.
이로부터 time step $t$에서의 출력 $y_t$는 이전 time step의 모든 입력에 대한 함수임을 알 수 있다. 즉, 각 time step에서의 출력은 이전까지의 입력을 보존하는 일종의 메모리 형태이며, 이러한 구조(time step에 걸쳐 어떤 상태를 보존하는 것)를 메모리 셀(Memory cell)이라고 정의한다. 즉, time step $t$에서의 (메모리)셀의 상태 $h_t$는
\[h_t = f(h_{t-1},x_t)\]로 나타낼 수 있다.
LSTM
LSTM이라고 불리는 Long short-term memory RNN은 앞서 설명한 형태의 일반적인 RNN 구조를 발전시킨 네트워크이다. 일반적인 RNN의 경우 레이어를 거치면서 데이터가 변환되므로, 입력 정보의 일부분은 훈련이 이루어질수록 사라지게 된다. 즉, 일정 수준에 이르러 첫 번째 입력에 대한 정보가 아예 사라질 수 있다. 이를 극복하기 위해 메모리 셀을 좀 더 복잡한 구조로 만들어 데이터의 장기 의존성을 보완하는 네트워크가 바로 LSTM이다. LSTM의 메모리 셀은 아래와 같은 구조로 이루어져있다.
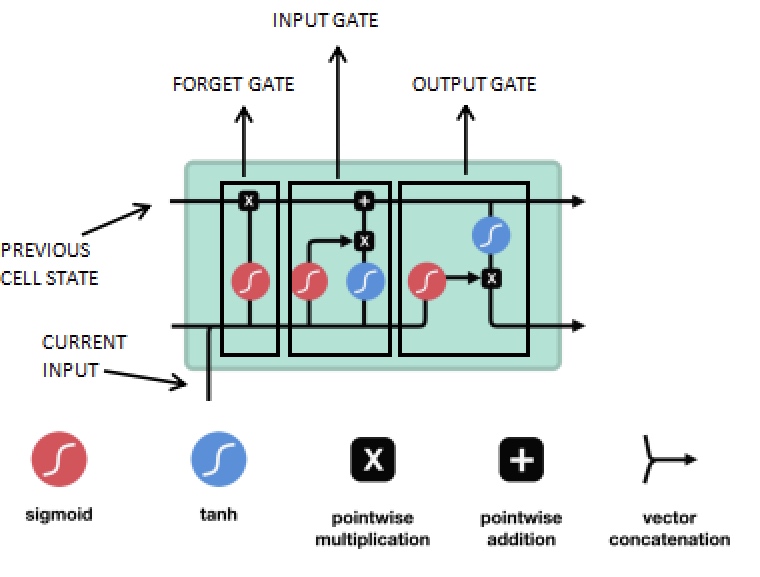
각 time step에서의 input($\mathbf x_t$)를 세 종류의 게이트(forget, input, output)에 각각 통과시켜 이전 셀의 상태(hidden vector $\mathbf h_{t-1}$와 memory vector $\mathbf m_t$)와 함께 처리한다. 구체적으로 time step $t$에서의 LSTM 셀에서는 다음과 같은 연산이 수행된다.
\[\begin{aligned} &\mathbf g^u = \sigma(\mathbf W^u\mathbf h_{t-1} + \mathbf I^u\mathbf x_t)\\ &\mathbf g^f = \sigma(\mathbf W^f\mathbf h_{t-1} + \mathbf I^f\mathbf x_t) \\ &\mathbf g^o = \sigma(\mathbf W^o\mathbf h_{t-1} + \mathbf I^o\mathbf x_t)\\ &\mathbf g^c = \tanh(\mathbf W^c\mathbf h_{t-1} + \mathbf I^c\mathbf x_t)\\ &\mathbf m_t = \mathbf g^f\odot\mathbf m_{t-1} + \mathbf g^u \odot \mathbf g^c\\ &\mathbf h_t = \tanh(\mathbf g^o \odot \mathbf m_t) \end{aligned}\]Convolutional Network
합성곱 신경망은 주로 이미지 처리 등에 사용되는 것으로 알려져있지만(참고), 2차원 합성곱 대신 1차원 합성곱(1D Convolution)을 사용하는 합성곱 신경망은 시계열을 다룰때 사용되기도 하는데 이를 temporal convolutional network라고도 한다. 합성곱 레이어의 연산이 데이터의 인접 원소간의 관계를 반영하기 때문에, 1차원 합성곱은 특정 time step을 기준으로 인접 time step의 입력을 반영할 수 있기 때문이다. Input feature vector가 $X_t\in \mathbb R^{F_0}$ 로 주어지고($l$번째 레이어의 벡터 길이를 $F_l$로 표기하자), 각 레이어에서의 time step 범위가 $0<t\leq T_l$ 로 주어진다고 하자(신경망의 연산 과정에서 시계열의 길이가 변화될 수 있음을 의미한다). 이때, 각 time step $t$에서의 $l$번째 레이어에 대한 출력벡터(activation function value) $\hat{\mathbf E}^{(l)}_t\in \mathbb R^{F_l}$ 의 i번째 성분은 다음과 같이 계산된다($d$는 filter duration, 즉 filter의 크기를 의미한다).
\[\hat{\mathbf E}_{i,t}^{(l)} = f\bigg(b_i^{(l)} + \sum_{t’=1}^d\big\langle W_{i,t’,.}^{(l)} , E^{(l-1)}_{.,t+d-t’}\big\rangle\bigg)\]LSTM-FCN
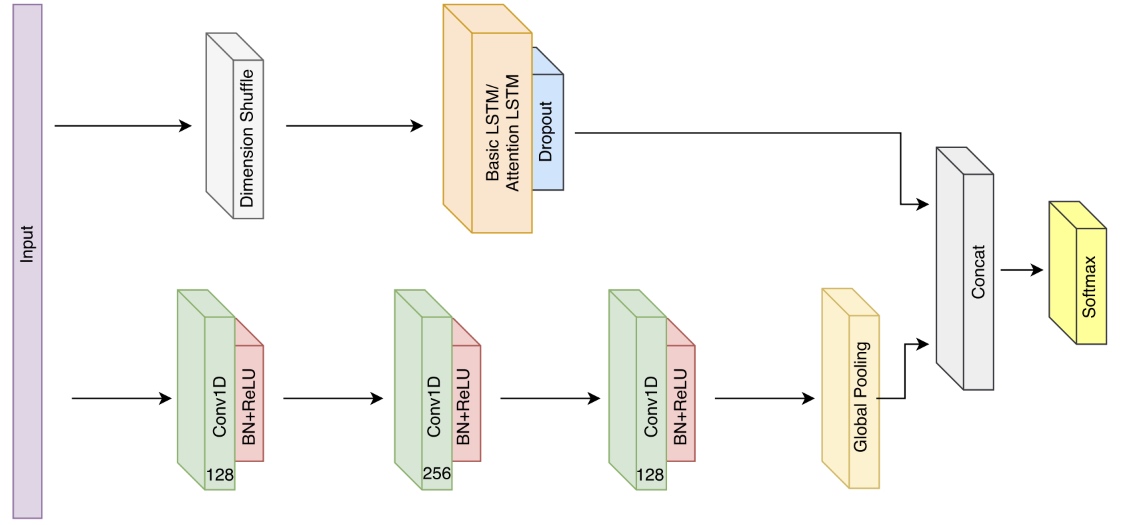
LSTM-FCN은 앞서 설명한 두 네트워크, LSTM-RNN과 Temporal Convolutional Network를 결합하여 시계열 분류에 활용가능하게 한 기법이다. 구조는 위 그림과 같은데(논문 참고), 먼저 Fully convolutional network(FCN)(그림 아래부분)이 feature extractor로서 기능한다. 이후 Global average pooling 레이어를 통해 분류 모델에서 사용되는 모수의 개수를 줄이게끔 한다. 또한, LSTM block을 이용해 그림과 같이 dropout을 추가하여 fully convolutional block을 향상시킨다. 논문에서는 각 convolutional layer 뒤에 batch normalization과 ReLU activation layer를 사용했으며, LSTM 이전에는 dimension shuffle layer를 이용하였다.
Dimension Shuffle
LSTM-FCN의 FCN 부분과 LSTM 부분은 모두 같은 input data를 입력받는다. 다만, 같은 시계열 데이터를 입력받아도 다른 관점에서 이를 처리한다. Fully convolutional block의 경우 길이가 $T$인 단변량(univariate) 시계열 데이터를 time step이 $T$인 데이터로 받는다. 반면 LSTM block은 같은 데이터를 time step이 1인(single time step), 변수가 $T$개 존재하는 다변량 시계열로 처리한다. 이러한 과정을 dimension shuffle이라고 하는데, 이 과정이 존재하지 않으면 LSTM block은 급격한 overfitting 문제로 long-term dependency를 학습하는데 실패하여 낮은 성능을 보이게 된다. 또한, 이러한 dimension shuffle은 네트워크의 학습 속도 향상에도 도움을 준다.
References
- Hands on Machine Learning, 2e.
- LSTM Fully Convolutional Networks for Time Series Classification, F. Karim et al. 2017.
Leave a comment