Multivariate LSTM-FCN

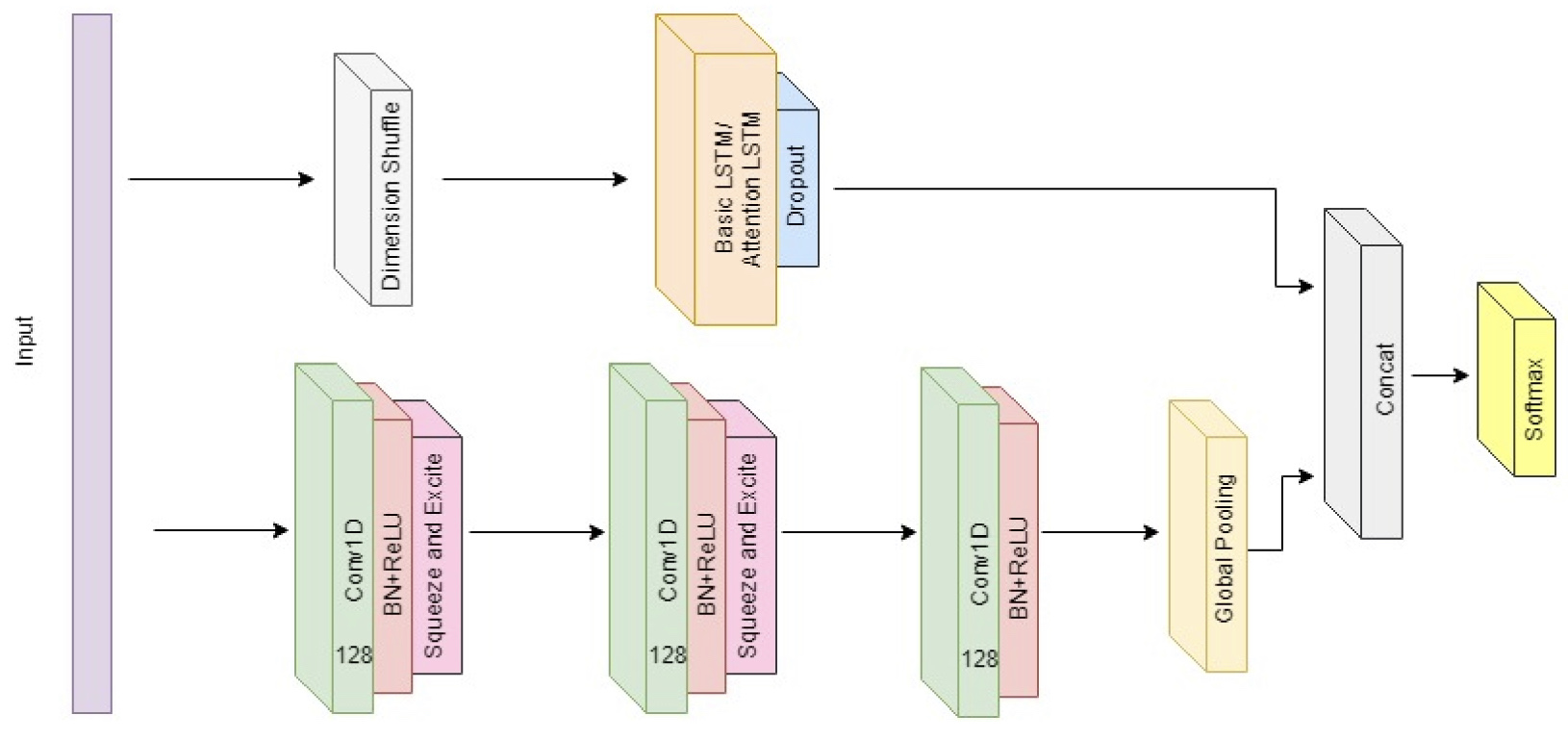
이번 글에서는 저번에 살펴본 단변량 시계열 분류모형인 LSTM-FCN을 다변량으로 확장한 Multivariate LSTM-FCN을 살펴보도록 할 것이다. 모형의 근본적인 구조는 LSTM-FCN과 동일하지만 convolutional layer들에서 Squeeze and Excite 라는 새로운 블록이 추가된다. Squeeze and Excite 블록은 본래 합성곱 신경망을 발전시키는 과정에서 고안된 네트워크인데 여기서는 LSTM-FCN의 합성곱 부분에 이를 응용한 것이다. 먼저, 네트워크의 전체 구조는 다음과 같다.

Squeeze-Excitation Block

Squeeze-Excitation block(SE block, Hu et al.)은 텐서의 변환 연산 $\mathbf F_{tr} : \mathbf X\to \mathbf U,\;\mathbf X\in\mathbb R^{W’\times H’\times C’},\mathbf U\in \mathbb R^{W\times H\times C}$ 에 대응하는 계산 블록(computational block)을 의미한다. 즉, 여기서 다루고자 하는 Convolutional network에 대해선 변환 연산 $\mathbf F_{tr}$은 합성곱 연산에 해당하며, SE block은 각 합성곱 블록에 대응하는 구조로 사용된다. Transformation $\mathbf F_{tr}$의 계산 결과는 $U = [\mathbf{u_1,u_2,\ldots,u}_C]$ 의 형태로 주어지는데, 각 성분벡터는

\[\mathbf u_c = \mathbf v_c\ast\mathbf X = \sum_{s=1}^{C’}\mathbf v_c^s \ast \mathbf x^s\]

으로 주어진다. 이때 연산 $\ast$는 합성곱 연산(convolution)을 의미하며, input data는 $\mathbf X = [\mathbf{x^1,\ldots,x^{C’}}]$로 나타냄을 의미한다. 또한, 전체 합성곱 연산(convolutional operator)은

\[\mathbf V = [\mathbf v_1,\ldots,\mathbf v_C]\]

로 주어지는데, 각 $\mathbf v_c$ 는 c번째 합성곱 필터를 의미하며, 필터의 각 채널(single channel)을 2차원 커널 $\mathbf v_c^s$로 나타난다. 위와 같이 정의되는 합성곱 블록에 대해, SE block은 Squeeze와 Excitation의 두 단계에 걸쳐 연산을 수행한다.

Squeeze

Squeeze block은 말 뜻 그대로 입력 벡터의 정보를 추출하며 차원을 축소시키는 계산인데, 이 과정은 전역 평균 풀링(global average pooling)을 이용한다. 이때 차원의 축소는 각 채널을 기준으로 이루어지는데, 앞서 언급한 feature map $\mathbf U$을 $\mathbf U$의 두 차원($H\times W$)으로 축소시켜 각 채널에 대한 통계량 $\mathbf z=\lbrace z_1,\ldots,z_C\rbrace \in \mathbb R^C$ 를 얻는다. 즉,

\[z_c = \mathbf F_{sq}(\mathbf u_c) = {1\over H\times W}\sum_{i=1}^H\sum_{j=1}^W u_c(i,j)\]

와 같이 얻어진다. 이렇게 얻어진 임베딩 벡터(embedding)은 아래 설명할 excitation 블록에 대입되어 다시 차원이 증강된다.

Excitation

앞서 Squeeze block을 통해 얻은 정보(임베딩) $\mathbf z$를 바탕으로, Excitation block에서는 채널간의 종속성(dependency)를 알아내는 것을 목표로 한다. 따라서 임베딩 $\mathbf z\in\mathbb R^C$ 성분(채널)간의 관계를 모수화하는 parameter $\mathbf W\in \mathbb R^{C\times C}$가 사용되어야 한다. 다만, 여기서 하나의 모수 행렬만 사용하게 되면 세 개 이상의 채널간의 상호작용(non-mutually-exclusive한 항)을 고려할 수 없으므로, 다음과 같이 두 개의 게이트(gate)로 구성하게 된다.

\[\mathbf s = \mathbf F_{ex}(\mathbf{z, W}) = \sigma(\mathbf W_2\cdot\rm{ReLU}(\mathbf{W_1z}))\]

이때 행렬 $\mathbf W\in\mathbb R^{C\times C}$는 두 행렬 $\mathbf W_1\in\mathbb R^{{C\over r}\times C}$와 $\mathbf W_2 \in \mathbb R^{C\times{C\over r}}$ 로 나뉘어진다. 이러한 방식으로 bottleneck 구조를 만드는 것은 모델의 복잡성을 제어하고 일반화를 돕기도 한다(bottleneck 정도는 reduction ratio $r$에 의해 결정된다).

다만, 위 식의 출력(activation)은 합성곱 블록의 출력형태와 일치하지 않으므로, rescaling 과정이 필요하다. 최종 출력 데이터가 $\tilde{\mathbf X} = [\tilde{\mathbf x_1},\ldots,\tilde{\mathbf x}_C]$ 로 표현될 때, 각 성분은 다음과 같이 얻어진다,

\[\tilde {\mathbf x}_c = \mathbf F_{scale}(\mathbf u_c,s_c) = s_c\mathbf u_c\]

여기서 $\mathbf u_c\in\mathbb R^{H\times W}$ 는 앞서 다룬 feature map(convolutional transformation)을 의미한다.

Squeeze-Excitation Block의 전체적인 흐름을 요약하면 다음 그림과 같다.

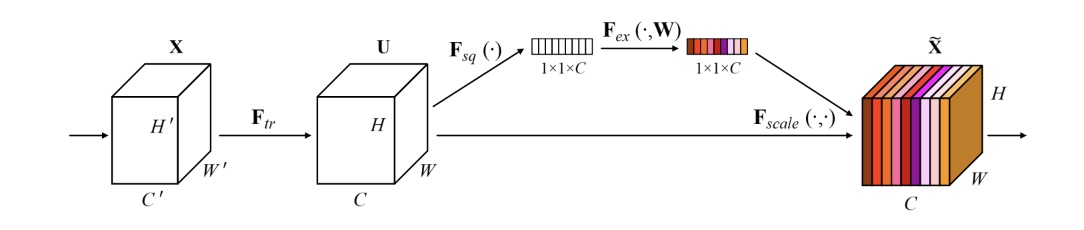
References

Squeeze and Excitation Networks, Hu et al.
Multivariate LSTM-FCNs for Time Series Classification, F.Karim et al. 2018.