Neural Networks

인공신경망Artificial Neural Network 이론은 2010년대부터 급속도로 성장한 머신러닝 분야 중 하나이다. 특히 이와 관련된 분야를 딥러닝이라고 하며, CPU 및 GPU의 성능이 비약적으로 향상되며 다른 머신러닝 기법들에 비해 그 성능이 급속도로 증가하고 있다. 이번 글에서는 인공신경망의 기초적인 내용에 대해 다루도록 하겠다.

Linear Classifier to Neural Network

LDA와 같은 선형분류기는 일반적으로 다음과 같은 형태를 취한다.

\[f=Wx\quad x\in\mathbb R^p,W\in\mathbf{M}_{C\times p}(\mathbb R)\]

즉, 클래스가 C개인 데이터셋을 분류할 때, $p$차원 데이터에 대해 parameter로 $C\times p$ 행렬 $W$가 주어진다. 가장 기초적인 인공신경망은 선형분류기에서 비롯된다. 아래 그림과 같은 2-layer neural network를 구현하는 상황을 보자. (신경망의 각 층을 layer라고 하며, layer 안의 각 성분들을 유닛unit 혹은 노드node라고 한다. 아래 신경망의 경우 3072개의 노드(이는 Input Vector의 차원과 같아야 한다.)로 이루어진 Input Layer와 100개의 노드로 구성된 1개의 Hidden layer, 마지막으로 클래스 개수인 10개의 노드로 구성된 Output layer로 구성된다.)

\[f=W_2h(W_1x)\]

그러면 그림과 같이 Input Vector를 hidden layer로 변환하는 행렬 $W_1$과 hidden layer에서 마지막 클래스별 점수로 변환하는 행렬 $W_2$가 필요할 것이다. (일반적으로 행렬 개수에 따라 Network의 layer 수를 말한다.) 다만, 이러한 신경망을 $f=W_2W_1x$ 로 표기하면 이는 선형분류기와 다를 바 없으므로 우리는 활성함수activation function라는 새로운 함수를 Layer에서 Layer 사이의 변환과정 마지막에 도입한다. 활성함수를 $h$로 표기하면, 2-layer Network는 다음과 같이 표현가능하다. 또한, 아래 그림과 같이 위 신경망은 한 레이어의 모든 노드가 다음 레이어의 모든 노드들과 연결되어있으므로, 이러한 형태를 fully-connected neural network라고 한다.

Activation Functions

활성함수에는 다양한 종류가 있는데, 일반적으로 다음 ReLURectified Linear Unit을 주로 이용한다.

\[h(x) = \max(0,x)\]

이밖에도 시그모이드sigmoid $\sigma(x)=1/(1+e^{-x})$, 하이퍼볼릭 탄젠트tangent hyperbolic $f(x) = \tanh(x)$ 등이 있다. 그렇지만 대부분의 딥러닝 문제에서(특히 Computer Vision같은 영역에서) 기본적으로 ReLU를 사용하며, 또한 문제의 특성(분류, 회귀) 등에 따라 주로 사용하는 함수가 바뀌기도 한다.

Optimization에서 살펴본 (Vanilla) Gradient Descent를 최적화 과정으로, 손실함수를 L2 loss function으로, 활성함수는 sigmoid function으로 설정한 간단한 2-layer 신경망을 numpy를 이용해 다음과 같은 코드로 보일 수 있다.

import numpy as np
from numpy.random import randn

N, Din, H, Dout = 64, 1000, 100, 10
x, y = randn(N, Din), randn(N, Dout)
w1, w2 = randn(Din, H), randn(N, Dout)
for t in range(10000):
  # Compute L2 Loss
  h = 1.0 / (1.0 + np.exp(-x.dot(w1)))
  y_pred = h.dot(w2)
  loss = np.square(y_pred - y).sum()
	# Compute Gradient
  dy_pred = 2.0 * (y_pred - y)
  dw2 = h.T.dot(dy_pred)
  dh = dy_pred.dot(w2.T)
  dw1 = x.T.dot(dh * h * (1 - h))
 	# Gradient Descent step
  w1 -= 1e-4 * dw1
  w2 -= 1e-4 * dw2

변수 N은 데이터 개수를, Din과 Dout은 각각 Input, Ouput Vector의 차원을 의미한다. H는 hidden layer의 노드 개수를 의미한다. 데이터는 난수로부터 생성되며, 초기 가중치행렬 w1,w2도 임의로 생성한뒤 10000번의 epoch동안 경사하강법을 실시한다.

Space Warping with ReLU

앞서 설명한 것과 같이 신경망이 복잡한 선형분류기와 구분될 수 있는 가장 큰 특징은 연산과정에서 활성함수가 이용된다는 것이다. 언뜻 생각해보면, 활성함수를 연산과정에 포함시키는 것이 큰 의미를 부여하는지 의문이 들 수 있다. 단지 선형분류기에 ReLU같은 함수를 취하는 것만으로도 제일 강력하다고 알려진 신경망이 작동한다는 의미이기 때문이다. 대표적인 함수 ReLU를 토대로 이를 자세히 살펴보자.

Linear Classifier는 선형변환 $h=Wx$ 을 의미한다. 이때 선형변환을 Data Space에서 Feature space으로의 mapping으로 생각할 수 있다(Kernel Theory 참조). 즉 아래 그림처럼 기존 두 개의 차원 $x_1,x_2$ 으로 주어지는 데이터들을 $h_1,h_2$ 차원으로 주어지는 특성공간으로 변환시키는 것이다.

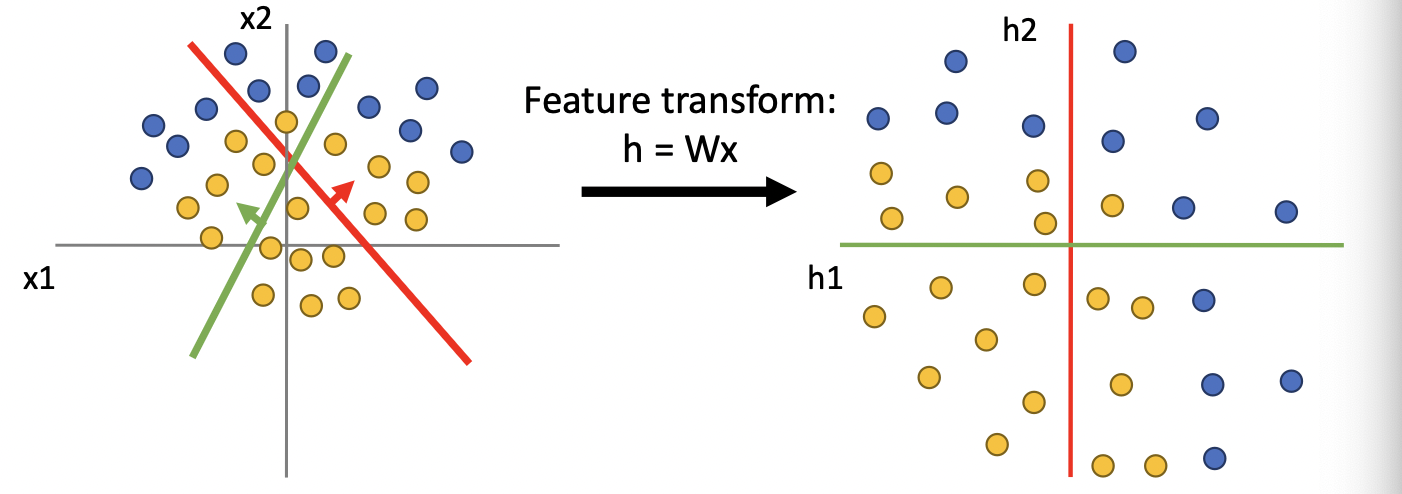
스크린샷 2022-03-12 오후 2.43.15

위 scatter plot에서는 왼쪽과 오른쪽 모두 두 개의 클래스를 linear한 형태로 분리할 수 없다. 반면, ReLU함수까지 취한 feature transformation을 생각해보면, ReLu는 0 이하의 값들에 대해 0의 값을 반환하므로, 데이터를 1사분면으로 변환시킨다. 따라서 아래 그림과 같이 Linearly separable한 특성공간이 만들어진다.

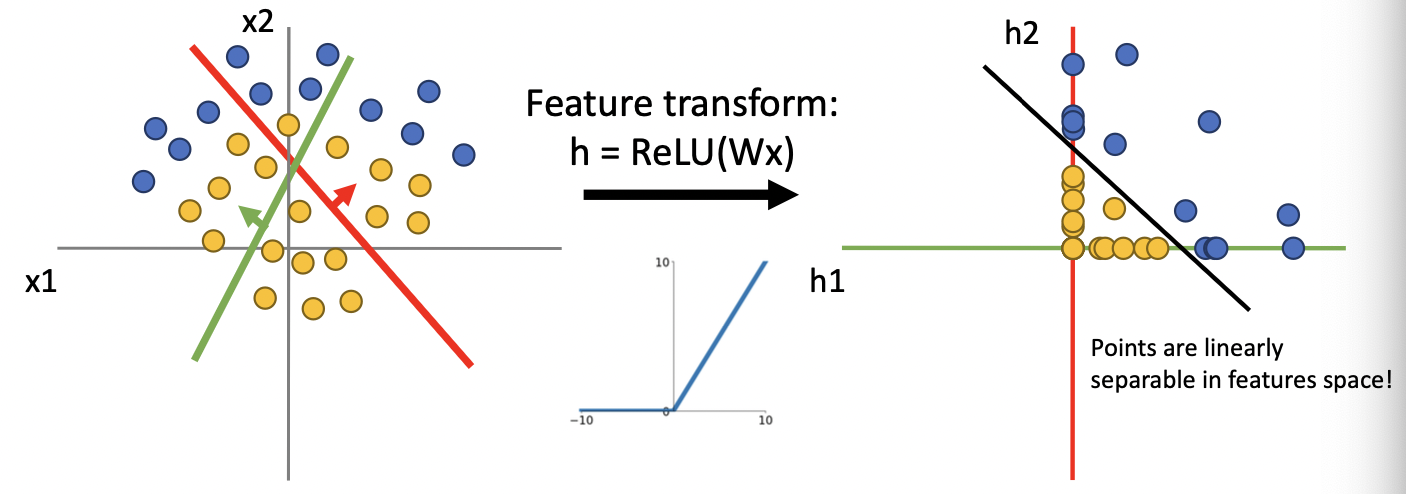
스크린샷 2022-03-12 오후 2.47.37

그런데 오른쪽 특성공간에서 만들어진 linear classifier은, 사실 원 데이터공간에서는 linear하지 않게 된다. 즉, 선형변환과 활성함수를 모두 적용한 feature transformation을 통해 non-linear한 decision boundary를 생성할 수 있다. 이는 곧 신경망을 통해 non-linear function을 근사할 수 있다는 말이고, 이러한 점이 인공신경망을 매우 강력하게 해준다.

Universality Theorem

바로 위에서 설명한 것 처럼 Neural Network는 사상 $f:\mathbb R^N\to\mathbb R^M$ 을 근사할 수 있게 해주는데, 이를 neural network의 universality라고 한다. Universality theorem을 증명하는 방법은 여러가지가 알려져 있는데, 리즈표현정리와 한-바나흐 정리를 이용한 방법이나 스톤-바이어슈트라스 정리를 이용하는 방법이 있다. 여기서는 간단한 추론을 통해 원리를 살펴보고자 한다. (더 수학적인 접근은 다른 글에서 별도로 다루도록 하겠다😅)

스크린샷 2022-03-12 오후 2.54.17

(심지어 위처럼 어떻게 생성했는지조차 모르는 🐶같이 생긴 함수도 근사가능하다 )

쉬운 설명을 위해 가장 간단한 형태인 $f:\mathbb R\to \mathbb R$ 만을 고려하도록 하자. 우선, 활성함수를 선택해야하는데 한 가지 주목해야 할 것은 모든 종류의 활성함수는 계단함수step function처럼 보이게 할 수 있다는 것이다.

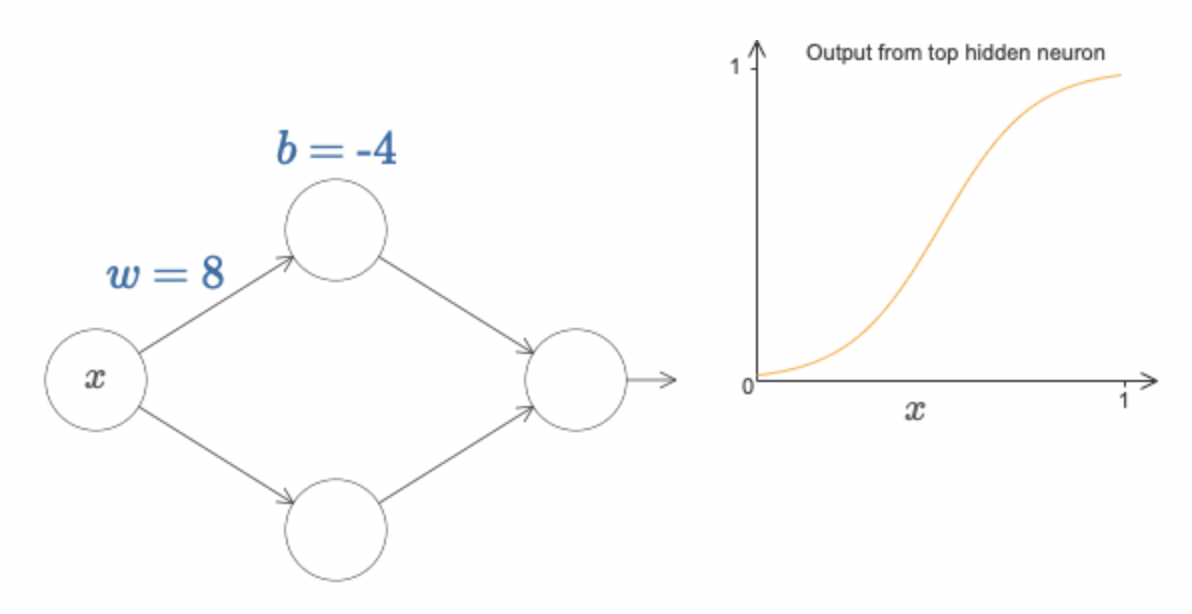
스크린샷 2022-03-12 오후 3.10.44

위 그림처럼 single layer network을 구성하고, 하나의 perceptron에서 $h(8x-4)$의 연산이 일어난다고 하자. 그러면 시그모이드 활성함수를 적용하면 input data $x$에 대해 오른쪽 그래프와 같은 연산이 일어난다. 그런데 만일 가중치와 편향값을 아래 그림처럼 크게(w=200, b=-100) 입력하면 perceptron 연산 $h(200x-100)$ 는 오른쪽 그래프와 같이 계단함수에 거의 근접하게 작동해버린다.

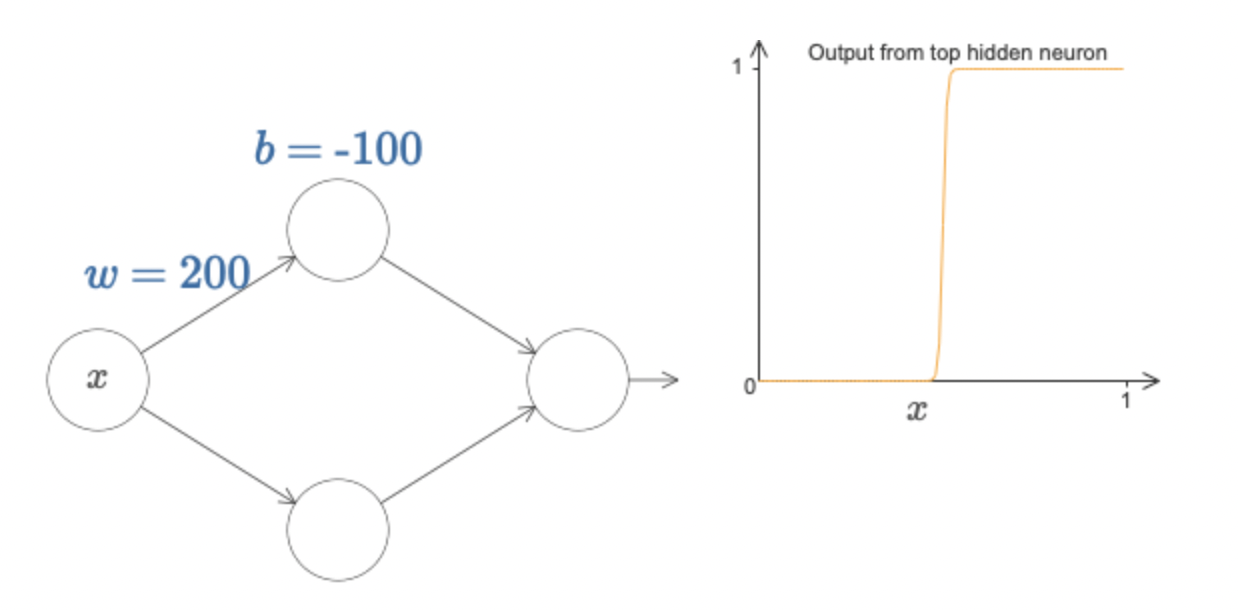
스크린샷 2022-03-12 오후 3.39.06

그렇다면, 각각의 hidden layer 노드들을 step function으로 생각하고 두 개의 노드 각각 $s_1, s_2$에서 step(함수값이 jump)이 일어난다고 하자. 또한 hidden layer에서 output layer로 이동할 때 역시 가중치가 적용되므로, 이를 각각 $w_1,w_2$로 생각하면

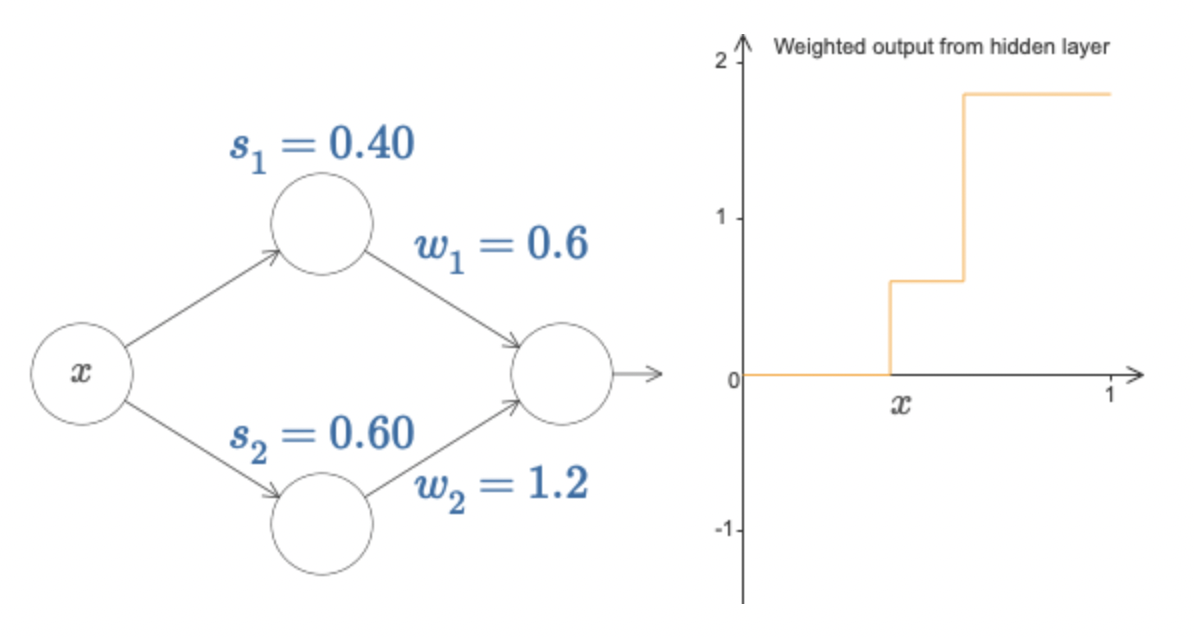
스크린샷 2022-03-12 오후 3.50.25

그림과 같이 두 개의 step function이 겹쳐진 형태를 취하게 된다. 그런데, 만일 output layer로의 두 가중치를 부호만 반대인 동일한 절대값을 취하게끔 하면

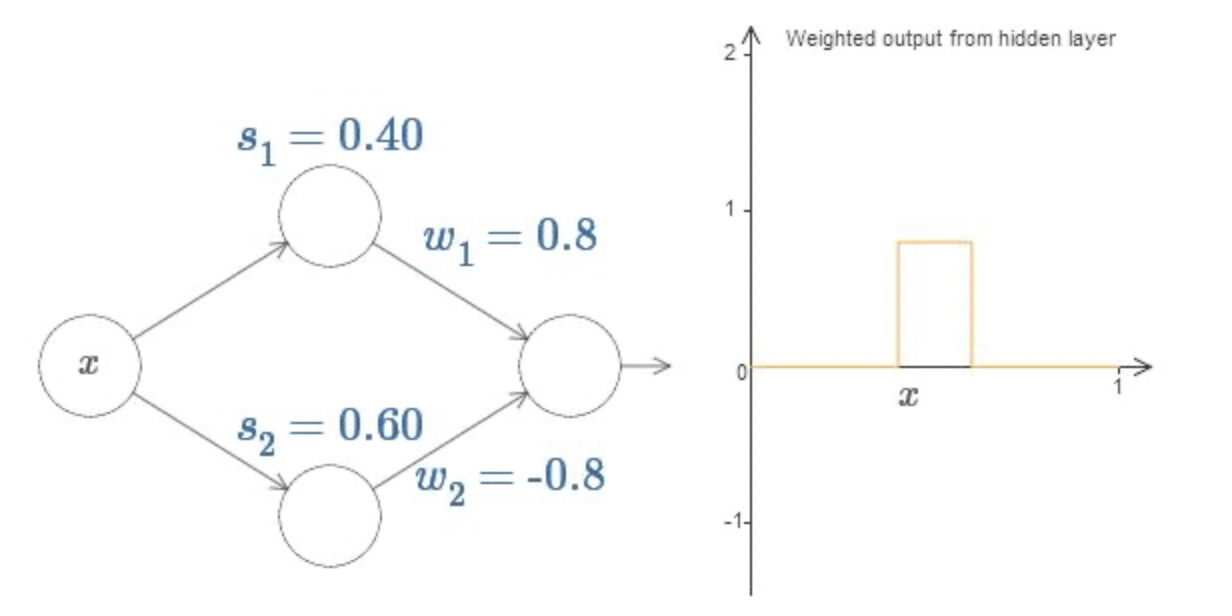
스크린샷 2022-03-12 오후 3.51.55

위 그림과 같은 형태의 함수를 얻는데, 이를 bump function이라고 한다. 이때 임의의 함수에 대해 hidden layer 개수를 늘리면서 bump function으로 근사함수를 취할 수 있는데, 이는 리만 적분의 기본적인 개념과 유사하다. 그런데 연속실함수는 리만적분가능하므로, 임의의 연속함수를 신경망 연산으로 근사할 수 있게되는 것이다. 마찬가지로, Input과 Output vector가 1차원이 아닌 경우 역시 Input/Output layer의 노드 수를 조정하고 bump function의 공간적 개념인 tower function을 통해 근사할 수 있다.

✅이는 일종의 유추에 의한 설명이고, 시그모이드 활성함수를 이용한 수학적인 증명은 다른 글에서 다루도록 하겠다.

References

  • Lecture note of “Deep Learning for Computer Vision”, UMich EECS

  • Hastie, T., Tibshirani, R., Friedman, J. H., & Friedman, J. H. (2009). The elements of statistical learning: data mining, inference, and prediction (Vol. 2, pp. 1-758). New York: springer.
  • ‘A visual proof that neural nets can compute any function’, M.Nielsen, 2019.

Leave a comment