Stochastic Optimization

Optimization

최적화^optimization과 관련된 내용은 통계학 및 머신러닝 뿐 아니라 다른 자연과학, 사회과학 분야들에서 널리 사용된다. 머신러닝 영역에서 최적화 문제는 다음 식 한줄로 표현할 수 있다.

\[w^{*}=\mathop{\arg\min}\limits_w L(w)\]

이때 argmin, 즉 최대화가 아닌 최소화 표현이 사용되는 이유는 머신러닝에서 사용하는 최적화는 손실함수 $L(w)$를 최소화하는데 초점이 맞춰져있기 때문이다(본격적으로 최적화를 다루는 convex optimization 영역에서도 함수의 convex와 일치하게끔 최소화로 치환하여 문제를 생각하는 경우가 많다). 손실함수는 squared loss function 뿐 아니라 softmax, SVM, Full loss function과 같이 딥러닝에서도 이용되는 다양한 종류가 있는데, 각각에 대해서는 추후에 더 살펴보도록 하겠다. 우선 여기서는 손실함수의 종류에 관계없이, 손실함수를 최소화하는 방법, 즉 알고리즘들에 대해 살펴보자.

Is Random Search🔍 an Optimization?

다음과 같은 알고리즘을 생각해보자.

bestloss = float("inf")
for num in range(1000):
  W = np.random.randn(10,3073)*0.0001
  loss = L(X_train, Y_train, W)
  if loss < bestloss:
    bestloss = loss
    bestW = W
 return bestW

위 알고리즘은 정해진 반복회수(1000번) 동안 임의의 W를 생성해 이에 대한 손실함수의 함수값(loss) 를 계산하고 기존까지의 최솟값보다 낮은 경우 이를 갱신하는 형태이다. 즉, 아무런 규칙 없이 최적화를 실행할 수는 있지만, 계산비용과 정확도 모두에서 너무 비효율적이기 때문에, 우리는 좀 더 체계적인 최적화 방식을 고안해야 한다.

Gradient Descent

Gradient

그래디언트^gradient는 벡터에 대해 정의된 미분계수이다. 즉, 일차원 유클리드공간에서의 함수

\[f:\mathbb{R}\to\mathbb{R}\]

에 대한 미분계수

\[\frac{df(x)}{dx}=\lim_{h\to0}\frac{f(x+h)-f(x)}{h} \tag{1}\]

와 유사하게, 손실함수 $L:\mathbb{R}^d\to\mathbb{R}$ 의 그래디언트는 각 성분의 편미분계수로 이루어진 $d$차원 벡터로 주어진다. (이계는 $d\times d$ 행렬로 주어지며 이를 Hessian Matrix^{헤시안행렬}이라고 한다.) 고교 수학과정에서의 간단한 개념으로 살펴보면, 어떤 점에서의 미분계수는 그 점에서의 접선의 기울기를 의미한다. 즉, 함수값이 그 점에서부터 어떤 방향으로 증가 혹은 감소하는지를 파악하게끔 해준다. 그래디언트도 마찬가지로 특정 차원(성분)에 대한 전체 함수값의 변화를 파악하는 도구이며, 이를 $\nabla_WL(W)$ 로 나타낸다.

이때 그래디언트를 구하는 것은 미분계수와 마찬가지로 두 가지 방법이 있다. 첫번째는 Analytic gradient로, 이는 우리가 도함수를 구하는 것과 마찬가지이며 함수를 변수들로 직접 미분(벡터 미분 등을 이용)히여 도함수를 구하고, 이에 구하고자 하는 점의 데이터를 대입해 그래디언트를 구한다. 반면, Numerical gradient는 미분계수의 정의 식 (1)에서 극한을 취하지 않고, $h$에 $10^{-3}$ 처럼 작은 값을 대입하여 수치적인 방식으로 빠르게 계산하는 것을 말한다. 따라서 일반적으로는 analytical gradient 를 사용하는 것이 맞고, 대개 이를 검산하기 위해 numerical gradient을 사용한다(이를 Gradient check 라고 한다).

Pytorch에는 gradient check를 위해 torch.autograd.gradcheck 와 그래디언트의 그래디언트를 check하기 위한 gradgradcheck 함수가 있다.

Gradient Descent

Gradient Descent 알고리즘은 그래디언트를 이용해 최적화를 진행하는 알고리즘이다. 아래 python 알고리즘을 살펴보자.

w = initialize_weights()
for t in range(num_steps):
  dw = compute_gradient(L, data, w)
  w -= eta * dw

위 알고리즘은 그래디언트를 이용한 가장 기초적인 알고리즘으로, 이를 Vanilla gradient descent라고도 한다. 식으로 표현하면 다음과 같다.

\[W=W-\eta\cdot\nabla_WL(W)\]

1차원 데이터셋에서 생각해보면, 어떤 점에서 미분계수가 양수라는 것은 그 점보다 작은 값에서 더 낮은 함수값을 취한다는 것이고 음수인 경우는 반대인 것이므로, 위 식에서처럼 그래디언트에 음수를 취하여 $w$를 갱신한다. 이때 학습률^{learning rate}을 의미하는 $\eta$ (eta)는 그래디언트를 얼마만큼 반영하여 갱신할 것인지를 의미하는 hyperparameter이다.

한편, 위와 같은 알고리즘을 batch gradient descent라고도 하는데, 이는 w값을 한번 갱신하기 위해 전체 데이터셋(data)에 대한 그래디언트를 통째로 계산하기 때문이다. (여기서 batch란 하나의 Loss function 값을 계산하는 데이터셋을 의미한다.) 그런데 데이터셋이 매우 큰 경우 계산비용^{computational cost}과 데이터를 임시저장할 RAM 리소스 등에 대한 부담이 과중된다. 따라서 이를 해결하기 위해 batch 크기를 축소하는 Stochastic gradient descent 알고리즘을 사용하게 된다.

Stochastic Gradient Descent(SGD)

SGD 알고리즘은 앞서 설명한대로 batch의 크기를 줄인 gradient descent 알고리즘을 의미한다. 쉬운 구분을 위해 batch의 크기가 작다는 의미에서 Mini-batch gradient descent라고 하며, batch 크기가 1인 경우만을 특별히 SGD라고 칭하기도 한다.

w = initialize_weights()
for t in range(num_steps):
  minibatch = sample_data(data, batch_size)
  dw = compute_gradient(loss_fn, minibatch, w)
  w -= learning_rate * dw

위 알고리즘은 SGD를 표현하는데, vanilla gradient descent과의 차이는 데이터셋에 대해 minibatch를 만들어 각각에 대해 그래디언트를 계산한다는 점이다. 이때 batch의 크기는 보통 32, 64, 128 같은 단위가 사용되는데 이는 크게 중요하지 않으며, GPU 등 연산처리환경이 감당할 수 있는 선에서 크게 설정하면 된다.

\[L(W)=\text{E}_{(x,y)\sim P(x,y)}[L(x,y,W)]+\lambda R(W)\tag{2}\]

우선 데이터셋 $(x,y)$가 확률분포 $P(x,y)$로부터 비롯되었다고 가정하고, 손실함수가 규제항 $R$을 포함한 형태로 식 (2)와 같이 주어졌다고 생각할 수 있다. 이때 기댓값은 표본평균으로 근사할 수 있으므로, 데이터 샘플 $\lbrace (x_i,y_i):i=1,\ldots,N\rbrace $ 에 대해 다음 식 (3)처럼 근사할 수 있다.

\[L(W)\approx{1\over N}\sum_{i=1}^NL(x_i,y_i,W)+\lambda R(W)\tag{3}\]

따라서 $L$에 대한 그래디언트 역시 다음과 같이 근사할 수 있다. 이처럼 손실함수를 전체 데이터셋의 확률분포에 대한 기댓값으로 가정한다는 의미에서 stochastic gradient descent 라고 한다.

\[\nabla_WL(W)\approx\sum_{i=1}^N\nabla_WL_W(x_i,y_i,W)+\nabla_W R(W)\]

Problems with SGD

SGD는 데이터 특성에 따라 최적화 과정에 문제가 발생할 수 있다. 데이터의 각 성분들에 대해, 어떤 차원에서는 가파르고(high derivative) 어떤 차원에서는 완만할(low derivative) 수 있다. SGD는 전체 데이터셋에 대한 그래디언트를 구하는 것이 아니라, 각 지점에서의 그래디언트를 구하는 것이므로 아래 그림처럼 가파른 성분에 대해서는 W의 변화가 크지만 완만한 성분에 대해서는 변화가 작아 최적화 과정이 매우 느려질 수 있다.

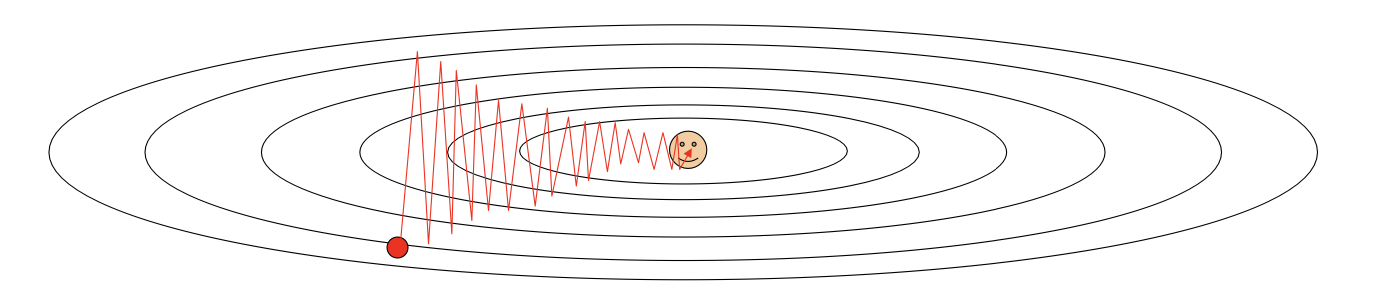
또한, 만일 손실함수가 Local Minimum이나 Saddle Point^안장점을 가진다면 이 역시 최적화가 일어나지 않을 수 있는데, 두 지점에서 그래디언트가 모두 $0$이므로 최적화가 멈추게 된다. 특히 saddle point는 한 성분에서 극소이고 다른 성분에서 극대인 상황을 의미하므로, 데이터 차원이 커질수록 saddle point의 형성 가능성이 더 높아진다. 따라서 이런 문제들을 해결하기 위해 새로운 방법을 고안하게 된다.

Improvement of SGD

SGD + Momentum

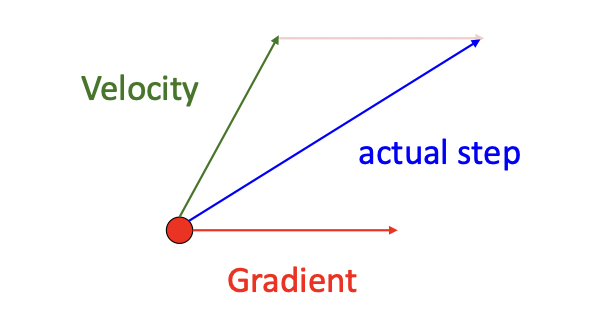
Momentum이란, 위 그림과 같이 SGD 진행과정에 운동량이 있다고 생각하고 그래디언트에 속도^velocity를 더해 최적화를 진행하는 과정을 의미한다(아래 그림).

v = 0
for t in range(num_steps):
  dw = compute_gradient(w)
  v = rho * v - eta * dw
  w += v

rho($\rho$)는 일종의 마찰^friction계수로 0.9, 0.99 등의 값을 갖는다. 위 알고리즘을 살펴보면 속도 v가 SGD의 진행에 따라 변화하는 것을 알 수 있는데, 이를 통해 local minimum 문제를 해결할 수 있다(지역최소에서 그래디언트는 0이지만 이전의 속도가 남아있기 때문).

AdaGrad

grad_squared = 0
for t in range(num_steps):
  dw = compute_gradient(w)
  grad_squared += dw * dw
  w -= learning_rate * dw / (grad_squared.sqrt() + 1e-7)

위와 같은 알고리즘을 AdaGrad라고 하는데, grad_squared 변수는 SGD가 진행될수록 각 지점에서의 그래디언트 제곱값들에 대한 누적합이다. 즉 점차 누적합이 증가하므로 이를 통해 SGD의 속도를 늦추게 된다. 그러나 최적화가 점차 늦어질수록 분모값이 커지므로 W의 학습률이 낮아지게 되고 결국 어느 순간부터는 최적점 도달 전 학습이 멈추게 된다. 이러한 문제를 해결하기 위해 RMSProp을 고안하게 된다.

RMSProp

grad_squared = 0
for t in range(num_steps):
  dw = compute_gradient(w)
  grad_squared += decay_rate * grad_squared + (1 - decay_rate) * dw * dw
  w -= eta * dw / (grad_squared.sqrt() + 1e-7)

RMSProp은 grad_squared를 누적하는 과정에서, decay_rate라는 변수를 설정해 일방적인 누적이 아닌 일부 값이 손실된 상태로 누적이 진행되게 된다. 이를 통해 AdaGrad의 시간 흐름에 따른 학습률 손실 문제를 어느정도 보완할 수 있게 된다.

Adam

Adam은 RMSProp에 앞서 설명한 Momentum 효과를 추가한 알고리즘으로, 딥러닝에서 사용되는 가장 기본적이고 대중적인 손실함수이다.

moment1 = 0
moment2 = 0
for t in range(num_steps):
  dw = compute_gradient(w)
  moment1 = beta1 * moment1 + (1 - beta1) * dw
  moment2 = beta2 * moment2 + (1 - beta2) * dw * dw
  w -= eta * moment1 / (moment2.sqrt() + 1e-7)

위 Adam 알고리즘에서 moment1은 위에서 설명한 momentum 효과를 위한 변수이며, moment2는 AdaGrad와 RMSProp에서 이용한 누적 그래디언트 제곱합을 의미하는 변수이다. beta1, beta2의 경우 주로 beta1=9.9, beta2 = 0.999 을 이용하고, 학습률 eta는 1e-3, 5e-4, 1e-4 등의 값을 이용한다.

Second-Order Optimization

Taylor Expansion을 이용하면 손실함수를 다음과 같이 근사할 수 있다.

\[L(W) \approx L(W_0) + (W-W_0)^\top\nabla_WL(W_0)+{1\over2}(W-W_0)^\top\mathbf{H}_WL(W_0)(W-W_0)\]

여기서 행렬 $\mathbf H_WL(W_0)$은 $W = W_0$에서의 헤시안 행렬을 의미한다. 이를 이용해 W을 다음과 같이 update할 수 있다:

\[W^{\ast} = W_0 - \mathbf H_WL(W_0)^{-1}\nabla_WL(W_0)\]

그러나 위 식에서 알 수 있듯 Hessian의 역행렬을 구하는 것은 $O(N^3)$의 연산이 필요하기 때문에, 데이터셋이 커질수록 연산이 과도해지며 데이터셋을 작게 하는 mini-batch 형태에서는 잘 작동하지 않게 된다. 그래서 Hessian의 역행렬 대신 이를 근사하는 BGFS 방법 등도 이차 최적화에 이용된다 (full batch update가 가능한 환경이라면 시도해볼수는 있겠다😅).

Practice

코드 연습은 아니지만 아래에 있는 프로그램을 통해 앞서 살펴본 일차 최적화 방법들의 최적화 경로 및 속도를 파악할 수 있다. 마우스로 한 지점을 누르면 그 점에서부터 왼쪽의 하얀 부분 (전역최소)와 오른쪽 하얀 부분(지역최소)으로의 최적화를 시행한다. 각 최적화 방법들을 비교해보자😃

See the Pen Untitled by dangchan (@dangchan) on CodePen.

References

An overview of gradient descent optimization algorithms, S.Ruder
Lecture note of “Deep Learning for Computer Vision”, UMich EECS
SGD code from here

Optimization

Is Random Search🔍 an Optimization?

Gradient Descent

Gradient

Gradient Descent

Stochastic Gradient Descent(SGD)

Problems with SGD

Improvement of SGD

SGD + Momentum

AdaGrad

RMSProp

Adam

Second-Order Optimization

Practice

References

Leave a comment