Cross Validation

Cross-Validation

Cross-validation^교차검증은 prediction error을 추정하는 과정에서 가장 널리 사용되는 방법 중 하나이다. 딥러닝을 포함한 대부분의 머신러닝 영역에서 기본적으로 교차검증을 사용하며, 또한 대부분의 패키지 역시 이와 관련된 메서드를 포함한다. 이번 글에서는 교차검증의 이론적인 내용을 살펴보도록 하자.

K-Fold Cross Validation

만일 어떤 머신러닝 알고리즘을 개발할 때 데이터가 매우 충분하다면, 우리는 임의로 Training set, Validation set, Test set을 각각 충분한 sample 수로 설정할 수 있을 것이다. 그러나 실제로는 데이터가 충분하지 않은 경우가 많으며, training 만으로도 벅찰 경우가 있다. 이런 경우를 해결하기 위해 전체 훈련 데이터셋을 $K$개로 나누어 ($K-1$)개 데이터셋으로 훈련을 하고, 이를 나머지 1개 데이터셋으로 검증하는 방법을 사용하는데 이를 K-fold cross validation이라고 한다.

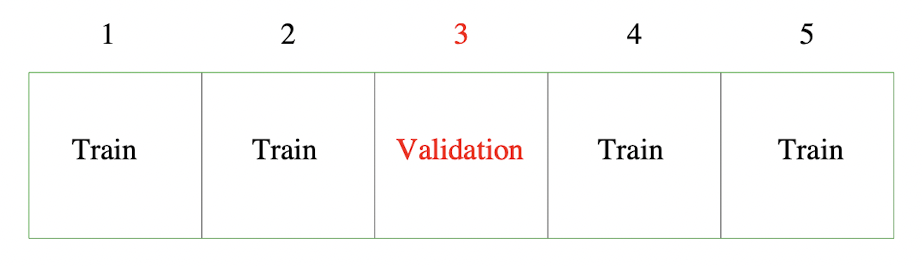
위 그림은 $K=5$인 CV를 나타내는데, $k=3$인 경우 나머지 $k=1,2,4,5$ 의 데이터를 이용해 모델을 훈련시키고, 이를 $k=3$인 부분의 데이터로 검증한다. 좀 더 일반적으로, 다음과 같은 인덱싱 함수(kappa)

\[\kappa:\lbrace 1,\ldots,N\rbrace \mapsto\lbrace 1,\ldots,K\rbrace\]

가 각 관측값($N$개)이 어떤 데이터셋($K$개)에 속하는지를 나타낸다고 하자. 또한, 함수 $\hat f^{-k}(x)$가 $k$번째 데이터셋이 제거된 채로 훈련된 모델이라고 정의하자. 이때 예측오차에 대한 cross-validation estimate를 다음과 같이 정의할 수 있다.

\[\text{CV}(\hat f) = {1\over N}\sum_{i=1}^N L(y_i,\hat f^{-\kappa(i)}(x_i))\]

만일 모델의 hyperparameter(tuning parameter) $\alpha$ 가 주어지는 경우, 모델을 $f(x,\alpha)$ 로 표기하고 $\hat f^{-k}(x,\alpha)$ 를 $k$번째 데이터셋을 제거하고 hyperparameter가 $\alpha$ 로 설정된 뒤 훈련된 모델이라 하자. 이때

\[\text{CV}(\hat f,\alpha) = {1\over N}\sum_{i=1}^N L(y_i,\hat f^{-\kappa(i)}(x_i,\alpha))\]

로 정의하면 $\text{CV}(\hat f,\alpha)$ 의 $\alpha$를 조절하며 test error curve를 얻을 수 있는데, 이를 바탕으로 적절한 tuning parameter $\hat\alpha$를 구할 수 있다.

어떤 K값을 사용해야 할까?

일반적으로 K-cross-validation의 K는 5 또는 10개를 설정하고, 특별히 $K=N$인 경우를 Leave-one-out cross-validation(LOOCV)이라고 한다.

$K=5,10$ 인 경우, 각 fold의 training set들이 원래 training set($N$ data)와 다르기 때문에 $\text{CV}(\hat f)$ 값은 Expected error($\text{Err}$, Test error의 기댓값)

\[\text{Err}=E_\mathcal T E_{X^0,Y^0}[L(Y^0,\hat f(X^0))\vert \mathcal T]\]

을 추정한다. 반면, LOOCV인 경우 cross-validation estimator($\text{CV}(\hat f)$) 값이 EPE(Expected prediction error)

\[\text{Err}(x_0) =E[(Y-\hat f(x_0))^2\vert X=x_0]\]

값의 근사적인 불편추정량^{unbiased estimator}이 된다. 그러나 EPE의 bias-variance decomposition에서 알 수 있듯이, 불편추정량 수준으로 편향이 낮아지는 만큼 분산이 증가하는데, 각 training dataset($N$개의 sets)이 서로 매우 유사하기 때문이다(임의의 두 training set은 $N-2$개의 데이터가 동일하므로).

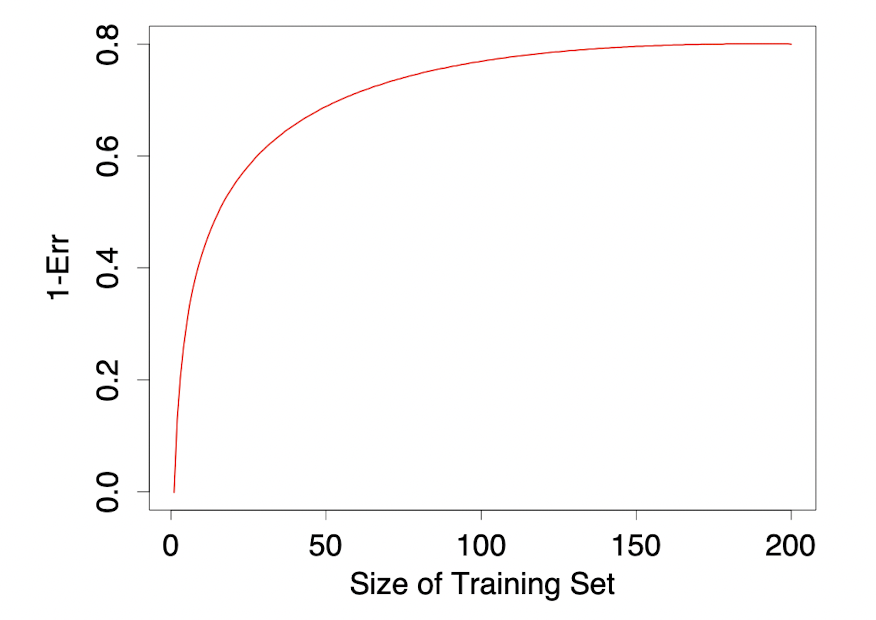
위 그래프는 어떤 분류 문제가 주어졌을 때 training set 크기에 따른 classifier의 $1-\text{Err}$ 값을 나타낸 가상의 learning curve이다. 여기서 training set의 크기는 $N\cdot\frac{K-1}{K}$, 즉 만일 $N=50$인 데이터셋에 5-fold CV를 적용할 경우 training set의 크기는 40이 된다. 이때 분류기의 성능은 크기가 100인 training set까지 증가하지만, 그 뒤로는 성능 증가폭이 미미하다. 반면, training set 크기가 50보다 작은 경우 해당 분류기는 $1-\text{Err}$을 제대로 추정하지 못하고(underestimation), 편향이 발생한다.

Generalized cross-validation(GCV)

LOOCV는 $N$개의 training set에 대해 모두 개별적인 연산을 요구하므로, 계산비용이 데이터셋의 크기에 비례해 증가한다. 이에 대해 GCV는 LOOCV에 대한 편리한 근사적 방법으로 사용되는데, 제곱오차에 대한 Linear fitting 문제에 대해 사용된다. 여기서 linear fitting은

\[\mathbf{\hat y=Sy}\]

꼴로 표현되는, linear regression을 포함한 모든 문제를 의미한다. 크기가 $N$인 데이터셋에 대해 LOOCV를 실행하고, 이때 $\hat f^{-i}$ 를 $i$번째 데이터를 제외한 training set에서의 모델의 추정치라고 하자. 그러면 LOOCV 전체 과정에 대한 Loss function은

\[\frac{1}{N}\sum_{i=1}^N[y_i-\hat f^{-i}(x_i)]^2\tag{1}\]

로 나타낼 수 있다. 이때 위 식 $(1)$은 아래와 같이 쓸 수 있다.

\[{1\over N}\sum_{i=1}^N\bigl[\frac{y_i-\hat f(x_i)}{1-S_{ii}}\bigr]^2\]

여기서 $S_{ii}$는 행렬 $S$의 $i$번째 대각성분을 의미한다. 이를 이용해 분모의 $S_{ii}$를 $\text{trace}(S)/N$ 으로 치환한 GCV 근사를 다음과 같이 정의한다.

\[\text{GCV}(\hat f)={1\over N}\sum_{i=1}^N\bigl[\frac{y_i-\hat f(x_i)}{1-\text{trace}(S)/N}\bigr]^2\]

각 대각성분 $S_{ii}$를 쓰지 않는 이유는, 어떤 $j$에 대해 $S_{jj}\approx1$ 인 상황인 경우 해당 항의 분모가 0에 수렴하여 값이 소위 튀어버리는 문제가 생길 수 있으므로, 이런 unstable함을 처리하기 위해 대각성분의 평균을 사용하는 것이다. 또한 이 경우 $S$의 각 대각성분을 계산할 필요 없이, 대각합만 구하면 되므로 대각합의 계산이 쉬운 상황에서는 계산적으로 LOOCV에 비해 큰 이점을 가질 수 있다.

References

• The Hastie, T., Tibshirani, R., Friedman, J. H., & Friedman, J. H. (2009). The elements of statistical learning: data mining, inference, and prediction (Vol. 2, pp. 1-758). New York: springer., 2e.