Gaussian Process Regression
Gaussian Process는 함수들의 사전분포에 대한 것이다. 이때, 함수들의 사전분포를 정하는 이유는 주어진 데이터로부터 함수를 추정하는 과정에서 특정 조건을 부여하여 추론 혹은 예측 과정을 더 용이하게 하기 위함이다. 이 과정에서 Gaussian, especially Multivariate Gaussian distribution을 사용하는 이유는 조건부 확률분포의 정규성 등 Gaussian distribution의 좋은 성질이 있기 때문이다.
Bayesian Approach for Linear Regression
Weight-Space View
다음과 같은 Linear Model을 고려하자.
\[Y = w^{T}X+\epsilon\quad \epsilon\sim N(0,\sigma_{n}^{2})\]베이지안적 관점에서, parameter $w$에 대한 사전분포를 다음과 같이 정규분포 형태로 줄 수 있다.
\[w\sim N(0,\Sigma_{p})\]그러면, 베이즈 규칙
\[\mathrm{posterior \propto likelihood \times prior}\]에 의해 posterior distribution을 다음과 같이 구할 수 있다.
\[p(w\vert X,Y)\propto\exp(- \frac{1}{2}(w-\bar w)^{T}(\frac{1}{\sigma_{n}^{2}}XX^T+\sigma_{p}^{-1})(w-\bar w))\]즉, posterior distribution 역시 정규분포를 따르는 것을 확인할 수 있고, 이로부터 posterior distribution의 평균이 $w$의 MAP(maximum a posteriori) estimate임을 알 수 있다.
Prediction
앞서 구한 사후분포를 바탕으로 새로운 test input data $x_{\ast}$에 대한 predictive distribution을 구하기 위해서는 다음과 같이 posterior에 대해 가능한 모든 선형모형의 평균을 취하는 방식을 사용한다.
\[\begin{aligned} p(f_{\ast}\vert x_{\ast},X,Y)&= \int p(f_{\ast}\vert x_{\ast},w)p(w\vert X,y)dw\\ &= N(\frac{1}{\sigma_{n}^{2}}x_{\ast}^{T}A^{-1}XY, x_{\ast}^{T}A^{-1}x_{\ast}) \end{aligned}\]Predictive distribution 역시 마찬가지로 정규분포를 따른다는 것을 확인할 수 있다.
Projection into Feature Space
일반적인 선형모형은 설명변수와 반응변수와의 관계를 오직 선형관계로만 파악해내기 때문에, 복잡한 구조를 갖는 데이터 형태에 대해서는 잘 적용되지 못한다는 한계점이 있다. 따라서 이를 극복하기 위해 Polynomial regression과 같은 분석방법을 채택하기도 하는데, 이러한 방법들의 공통점은 선형모형의 사용과정에서 우선 Input data를 high-dimensional feature space에 project한다는 것이다. 예를 들면, polynomial regression의 경우 데이터를 $\phi(x)=(1,x,x^{2},x^{3},\ldots )$에 사영시킨 것이다. 이 경우 새로운 선형모형은 다음과 같다.
\[Y= f(X)+\epsilon \qquad f(\mathbf{x})=w^{T}\phi(\mathbf{x})\]이를 이용하면 predictive distribution은 다음과 같이 주어진다.
\[f_{\ast}\vert \mathbf{x}_{\ast},X,Y\sim N(\phi_{\ast} ^{T}\Sigma_{p}\Phi(K+\sigma_{n}^{2}I)^{-1}Y, \phi_{\ast}^{T}\Sigma_{p}\phi_{\ast}-\phi_{\ast}^{T}\Sigma_{p}\Phi(K+\sigma_{n}^{2}I)^{-1}\Phi^{T}\Sigma_{p}\phi_{\ast} )\]이 과정에서 등장하는 내적 형태의 함수 $k(\mathbf{x,x’})=\phi(\mathbf{x})^{T}\Sigma_{p}\phi(\mathbf{x’})$ 를 kernel이라 정의한다.
Function-space View
앞서 살펴본 방식은 선형모형의 모수 $w$에 대한 사전분포를 바탕으로 사후분포를 구하고, 이를 이용한 예측 과정이었다. 반면, 다음과 같이 모형을 가정하는 대신에, 함수의 (사전)확률분포인 Gaussian Process를 고려하여 새로운 데이터에 대한 예측 모형을 만들 수 있다($m(x)$는 일반적으로 0).
\[Y=f(X)+\epsilon\qquad f(X)\sim GP(m(x),k(x,x'))\]Gaussian process는 정의에 의해 임의의 input point들의 finite subset $X_{n}=\lbrace x_{1},\ldots,x_{n}\rbrace $ 에 대한 evaluation $f(x_{1}),\ldots,f(x_{n})$ 이 Multivariate gaussian distribution을 따르므로, 다음과 같이 주어진 Gaussian process로 부터 random Gaussian vector를 생성할 수 있다.
\[\mathbf{f}_{\ast}\sim N(0,K(X_{\ast},X_{\ast}))\]여기서 공분산행렬은 임의의 input data의 부분집합 $X_{\ast}$에 대한 kernel matrix를 의미한다(input data가 feature space보다 높은 차원을 가지면 singular matrix가 됨).
Prediction
주어진 사전분포 $GP(m,K)$로부터 random function을 생성하는 것에 그쳐서는 회귀분석을 진행할 수 없다. 추가적으로 실제 관측된 데이터가 주는 정보들을 해당 사전분포에 결합시키는 과정이 필요하다. 관측치 $(x_{1},y_{1}),\ldots,(x_{n},y_{n})$ 이 주어질 때, 모형
\[y=f(x)+\epsilon\qquad \epsilon\sim N(0,\sigma^{2})\]에 대해 $f$를 추정하고 이를 바탕으로 새로운 test data $X_{\ast}$에 대한 output vector $\mathbf{f}_{\ast}$를 예측해야 하는 문제를 생각해보자. 우선 함수 $f$는 Gaussian process $GP(0,K)$ 를 따른다고 설정하면 관측치 $X$에 대한 evaluation은 random gaussian vector
\[\mathbf{f} \sim N(0,K(X,X))\]가 된다. 이로부터 관측치 $Y$의 분포는
\[Y\sim N(0, K(X,X)+\sigma^{2}I_n)\]이 된다. 그러면 $Y$와 prediction output vector $\mathbf{f}_{\ast}$의 결합분포는
\[\begin{pmatrix}Y\\ \mathbf{f}_{\ast}\end{pmatrix} \sim N\bigg( \mathbf{0}, \begin{pmatrix}K(X,X) + \sigma^{2}I & K(X,X_{\ast}\\ K(X_{\ast},X) & K(X_{\ast}, X_{\ast})\end{pmatrix} \bigg)\]와 같다. 정규분포의 조건부확률분포 공식을 이용하면 다음과 같이 Gaussian process regression equation을 얻을 수 있다.
\[\begin{aligned} \mathbf{f}_{\ast}\vert X,Y,X_{\ast} &\sim N(\bar{\mathbf{f}_{\ast}},\mathrm{cov}(\mathbf{f}_{\ast}))\\ \bar{\mathbf{f}_{\ast}} &= K(X_{\ast},X)[K(X,X)+\sigma^{2}I]^{-1}Y\\ \mathrm{cov}(\mathbf{f}_{\ast})&= K(X_{\ast},X_{\ast})-K(X_{\ast},X)[K(X,X)+\sigma^{2}I]^{-1}K(X,X_{\ast}) \end{aligned}\]Prediction for single point
앞서 구한 prediction equation을 하나의 $x_{\ast}$에 대한 예측값을 구하는 과정에 사용해보면 다음과 같다.
\[\begin{aligned} \bar f_{\ast}&= \mathbf{k}_{\ast}^T(K+\sigma^{2}I)^{-1}Y\\ \mathrm{Var}(f_{\ast})&= k(x_{\ast},x_{\ast})-\mathbf{k}_{\ast}^{T}(K+\sigma^{2}I)^{-1}\mathbf{k}_{\ast} \end{aligned}\]여기서 $\mathbf{k}$는 test point $x_*$와 n개의 training point 간의 커널함수값으로 이루어진 n-dimensional 벡터이다. 이때 예측치의 평균함수가 $Y$의 선형결합으로 이루어져있음을 확인할 수 있는데, 실제로는 다음과 같은 n개의 kernel function의 선형결합 꼴로 나타낼 수 있다.
\[\bar f_{\ast}=\sum_{i=1}^{n}\alpha_{i}k(x_{i},x_* )\]Algorithm
# RBF kernel
def kernel(a, b, param):
sqdist = np.sum(a**2, 1).reshape(-1, 1) + np.sum(b**2, 1) - 2*np.dot(a, b.T)
return np.exp(-0.5 * (1/param) * sqdist)
# noise level
noise = 0.1
# Computing Algorithm
L = np.linalg.cholesky(K + noise*np.eye(N))
alpha = np.linalg.solve(L.T, np.linalg.solve(L, y))
# test points
Xtest = np.linspace(-5, 15, 100).reshape(-1, 1)
Ktest = kernel(X.reshape(-1, 1), Xtest, param)
ytest = np.dot(Ktest.T, alpha) # prediction values
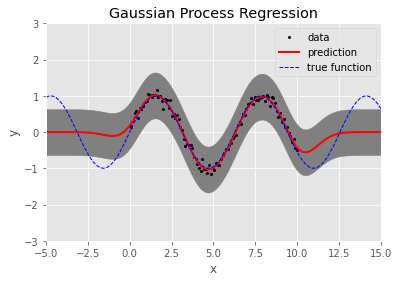
100개의 임의 생성 데이터에 대한 결과는 다음과 같다.
References
- C. E. Rasmussen - Gaussian Process for Machine Learning
- Code on Github
Leave a comment