Mixture Model

Mixture Model & EM Algorithm

Mixture Model

Mixture Model은 Latent Variable Model(LVM)의 일종이다. 여기서 LVM은 관측된 변수들간의 상관관계를 숨겨진 공통원인(common cause)에서 비롯된 것으로 가정한 모델이다. LVM을 이용하면, 차원축소(ex. PCA)를 수행하는 것과 같이 하나의 공통변수에 여러 기존 변수들을 대응시켜 모델을 축소할 수도 있다.

Mixture Model은 LVM의 가장 간단한 형태이다. 여기서는 잠재변수를 이산형 확률변수로 설정한다. 즉, 각 잠재변수는

\[z_i\in\lbrace 1,2,\ldots,K\rbrace\]

으로 표현된다. 이로부터 사전분포를 이산형인 $p(z_i)=\text{Cat}(\mathbf\pi)$ 형태로 두고, 가능도함수의 경우 $p(\mathbf x_i\vert z_i=k) = p_k(\mathbf x_i)$ 로 둔다. 여기서 $p_k$는 관측값들에 대한 $k$번째 base distribution이고, 이는 어떠한 종류의 확률분포이든 가능하다. 이로부터 다음과 같은 Mixture Model을 생성할 수 있다.

\[p(\mathbf x_i\vert \theta) = \sum_{k=1}^K\pi_kp_k(\mathbf x_i\vert \theta)\]

각 $\pi_k$ 에 대해서는 $0\leq\pi_k\leq 1, \sum_k\pi_k = 1$ 을 만족한다.

Gaussian Mixture

가장 널리 쓰이는 Mixture model은 base distribution을 정규분포로 하는 Gaussian Mixture Model이다(GMM). 즉, k개의 정규분포를 결합하여 만든 모델로, 다음과 같다.

\[p(\mathbf x_i\vert \theta) = \sum_{k=1}^K\pi_k\rm{N}(\mathbf x_i\vert \mu_k,\Sigma_k)\]

Parameter Estimation

앞서 살펴본 Mixture Model들에서 이번에는 Dataset $\mathcal D$가 주어졌을때 모수를 추정하는 방법에 대해 생각해보자. GMM의 경우로 살펴보도록 하자. 먼저, 만일 잠재변수 $z_i$들이 모두 관측된다고 가정하면, 사후분포는 다음과 같이 주어진다.

\[p(\theta\vert \mathcal D) = \text{Dir}(\pi\vert \mathcal D)\prod_{k=1}^K\text{NIW}(\mu_k,\Sigma_k\vert \mathcal D)\]

이는 unimodal한(단봉형의) 분포이므로, 전역최적값이(MAP/MLE) 존재한다.

Unidentifiability

문제는 잠재변수들이 관측되지 않는다는 점인데, 이 경우 각각의 잠재변수 $z_i$ 에 대해 서로 다른 unimodal likelihood가 존재한다. 예시로 다음 Plot을 살펴보자.

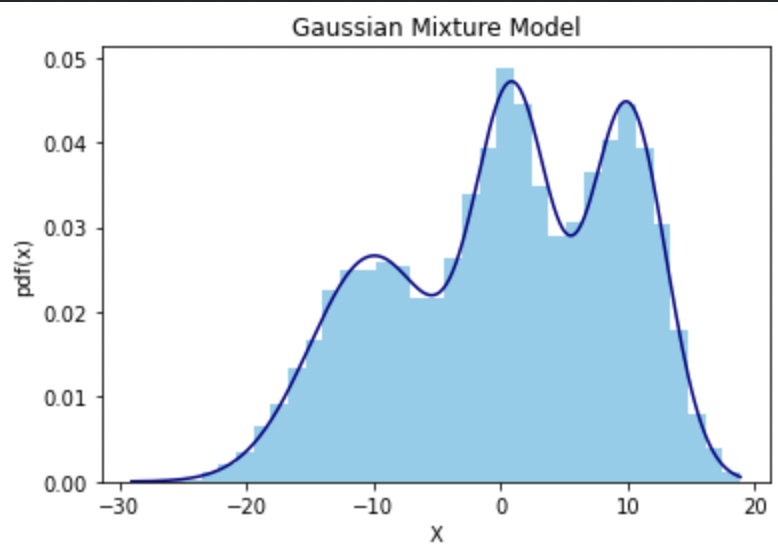
위 히스토그램과 밀도함수(pdf)는 서로 다른 세 개의 정규분포를 동일한 weight(1/3)으로 혼합한 모형이다. 각 정규분포는 $(\mu,\sigma)\in\lbrace (-10,5),(1,3),(10,3)\rbrace $의 모수를 갖는 것으로 설정하였다. 역으로 생각해보면, 위 plot과 같은 혼합 모형이 주어졌을 때 각 모수 $\mu_1,\mu_2,\mu_3$ 이 각각 -10, 1, 10에 대응한다고 장담할 수는 없다. $(-10, 1, 10)$ 혹은 $(1, -10, 10)$ 으로 주어지는 경우 모두 같은 weight를 가지는 한 동일한 혼합모형을 형성하기 때문이다. 이러한 성질을 Not Identifiable하다고 하며, 이 경우 사전분포에 대해 각 모수의 라벨(1,2,3)을 특정할 수 없으므로($K!$개의 경우의 수가 존재한다) 유일한 MAP 추정량이 존재하지 않는다.

이를 해결하기 위한 방법으로는 MCMC나 Local Mode에서의 (approximate) MAP estimate를 찾는 방법 등이 존재한다.

EM Algorithm

Gaussian Mixture model을 비롯해 많은 머신러닝 모델들에 대해, 만일 모든 데이터와 확률변수들이 관측될 수 있다면 MLE나 MAP 추정량을 구하는 것은 간단한 문제이다. 그러나 Mixture model과 같이 잠재변수가 존재하거나, 결측치가 있는 문제의 경우 이는 간단하지 않다. 이를 해결하기 위해 EM(Expectation-Maximization) 알고리즘이 사용되는데, 이에 대해 살펴보도록 하자.

Definition

추정량을 구하는 과정은 다음과 같은 로그가능도를 최대화하는 것이다.

\[l(\theta) = \sum_{i=1}^N \log p(\mathbf x_i\vert \theta) = \sum_{i=1}^N\log\bigg[\sum_{\mathbf z_i} p(\mathbf{x_i, z_i\vert \theta})\bigg]\]

여기서 $\mathbf x_i$들은 관측가능한 변수들이며 $\mathbf z_i$들은 결측변수 혹은 잠재변수를 의미한다. 그러나 위 가능도는 최적화하기가 어렵기 때문에, EM 알고리즘은 이를 일부 변형한다.

우선 다음과 같이 complete data 로그가능도를 정의한다.

\[l_c(\theta) = \sum_{i=1}^N \log p(\mathbf x_i,\mathbf z_i\vert \theta)\]

하지만 위 가능도함수에서 잠재변수에 대한 정보가 없기 때문에, 기댓값 형태인 expected complete data log likelihood를 다음과 같이 정의한다.

\[Q(\theta,\theta^{t-1}) = \mathrm{E}[l_c(\theta)\;\vert \;\mathcal D,\theta^{t-1}]\]

여기서 $t$는 알고리즘의 현재 반복 횟수이며, $Q$는 auxiliary function이다.

알고리즘은 E step과 M step으로 구성되는데, E 단계에서는 위 auxiliary function을 계산하는 과정이다. 이후 M 단계에서는 다음과 같이 $Q$를 최대화하는 모수를 찾아 update가 이루어진다.

\[\theta^t = \arg\max_\theta Q(\theta,\theta^{t-1}) \;:\;\text{MLE} \\ \theta^t = \arg\max_\theta Q(\theta,\theta^{t-1}) +\log p(\theta)\;:\;\text{MAP}\]

EM for Gaussian Mixture Models

$K$개의 가우시안 분포를 혼합한 GM 모델에 대해 EM 알고리즘이 어떻게 적용되는지 살펴보도록 하자. 우선, auxiliary funciton(expected complete data log likelihood)는 다음과 같이 주어진다.

\[\begin{aligned} Q(\theta,\theta^{t-1}) &= \mathrm E\bigg[\sum_i \log p(\mathbf x_i,z_i\vert \theta)\bigg]\\ &=\sum_i\mathrm E\bigg[\log\bigg[\prod_{k=1}^K(\pi_kp(\mathbf x_i\vert \theta_k))^{\mathrm I(z_i=k)}\bigg]\bigg]\\ \cdots &= \sum_i\sum_k r_{ik}\log\pi_k + \sum_i\sum_k r_{ik}\log p(\mathbf x_i\vert \theta_k) \end{aligned}\]

여기서 $r_{ik} = p(z_i=k\vert \mathbf x_i,\theta^{t-1})$ 로 정의되는데, 이는 i번째 데이터가 k번째 클러스터(k번째 정규분포)에 포함될 확률이다(responsibility라고 정의한다).

E step

E step에서는 위 expected function을 계산하는 과정이 이루어지는데, 어떤 종류의 mixture model에 대해서든 다음과 같이 responsibility function이 계산된다.

\[r_{ik} = \frac{\pi_kp(\mathbf x_i\vert \theta_k^{t-1})}{\sum_{k'}\pi_{k'}p(\mathbf x_i\vert \theta_{k'}^{t-1})}\]

M step

M step에서는 앞서 구한 $Q$를 weight $\pi$와 parameter $\theta_k$에 대해 최적화한다. 먼저 $\pi$에 대한 최적값은

\[\pi_k = {r_k\over N}\]

으로 주어지고 $\theta_k=(\mu_k,\Sigma_k)$ 에 대한 최적값을 구하기 위해서는

\[\begin{aligned} l(\mu_k,\Sigma_k) &= \sum_k\sum_i r_{ik}\log p(\mathbf x_i\vert \theta_k) \\ &= -{1\over 2}\sum_i r_{ik}[\log\vert \Sigma_k\vert + (\mathbf x_i-\mathbf \mu_k)^T\Sigma_k^{-1}(\mathbf x_i-\mathbf \mu_k)] \end{aligned}\]

으로부터

\[\mu_k = {\sum_i r_{ik}\mathbf x_i\over r_k}\\ \Sigma_k = {\sum_i r_{ik}\mathbf x_i\mathbf x_i^T\over r_k} - \mu_k\mu_k^T\]

를 얻을 수 있다. 이 과정을 반복하여 EM algorithm의 추정량을 찾을 수 있다.

References

• Machine Learning - A Probabilistic Perspective, K.Murphy
• Code at Github : https://github.com/ddangchani/Velog/blob/main/Statistical%20Learning/MixtureModels.ipynb