Random Forest
Random Forest
Random Forest는 Bagging배깅 방식을 이용한 Tree algorithm의 일종이다. 즉, 서로 상관관계가 없는 (de-correlated, randomized) tree들을 매우 많이 생성하여, 이들의 평균값을 바탕으로 분류 혹은 회귀를 진행하는 알고리즘이다. Tree model이 Bagging algorithm을 실행하는데 가장 최적인 이유는 데이터 내부의 복잡한 상호작용을 확인할 수 있으며 tree를 깊게 만들수록 낮은 bias를 가지는 모델이 되기 때문이다. 또한, Tree는 noisy한 특성이 있기 때문에, 여러 tree들의 평균치를 구하는 것은 noise들을 제거할 수 있다는 점에서 의미있고, 이는 한 Tree의 기댓값으로도 의미있는 수치이다.
✅ Bagging vs. Boosting
Bagging : Bootstrap Aggregating의 줄임말로, Bootstrap sample을 이용해 여러 모델을 생성하고 이들의 평균을 통해 예측값을 구하는 방법이다. Random Forest는 이러한 Bagging 방식을 이용한 Tree model의 일종이다. (각 모델이 서로 독립)
Boosting : 앞서 언급한 Bagging과는 다르게, Boosting은 weak classifier를 순차적으로 학습시켜 예측값을 개선시키는 방법이다. 이는 각 classifier의 결과를 이용해 다음 classifier의 결과를 개선시키는 방식으로 진행된다. (각 모델이 독립이 아님)
Ensemble : 여러 모델을 결합하는 방법으로, Bagging과 Boosting은 이러한 Ensemble 방법의 일종이다.
Algorithm
Random Forest 모형의 전반적인 알고리즘은 다음과 같다.
For $b=1,\ldots,B$ (Bootstrap size):
1) Training data에서 size $N$인 Bootstrap sample $\mathbf Z^{\ast}$를 추출한다.
- $\mathbf Z^{\ast}$에 대한 random-forest tree $T_b$를 생성하는데, terminal node에 대해 다음 과정들을 반복하여 terminal node의 크기가 최소 노드 사이즈인 $n_{min}$이 될 때 Tree의 생성을 중단한다.
- $p$개의 변수 중 $m$개의 변수를 랜덤하게 선택한다.
- $m$개의 변수 중 최선의 변수와 split-point를 선택한다.
- 해당 노드를 두개의 daughter node로 분할한다.
- Tree들의 Ensemble \(\lbrace T_b\rbrace _1^B\) 를 출력한다.
새로운 데이터 $x$에 대한 예측값으로 다음을 사용한다.
- Regression : $\hat f^B(x) = {1\over B}\sum_{b=1}^B T_b(x)$
- Classification : $\hat C^B(x)=\text{mode of }\lbrace \hat C_b(x)\rbrace _1^B$
이러한 알고리즘으로 생성된 Random Forest model은, 개별 트리들에 비해 비슷한 편향을 가지지만 분산은 더 낮게끔 개선된 결과를 갖는다. Adaptive한 방법으로 편향의 개선이 이루어지는 Boosting 알고리즘과는 다르게, RandomForest의 개별 트리들은 모두 Bootstrap 방식으로 이루어진 i.i.d 한 확률변수이다. 그러므로, 만약 개별 트리들이 분산 $\sigma^2$를 갖는다면 $B$개의 트리들의 평균인 RandomForest의 분산은 $\sigma^2/B$가 된다.
그러나, 만일 개별 트리들이 i.didentically distributed인 경우 각각의 트리 간에 상관계수 $\rho$가 존재한다면 RandomForest의 분산은
\[\rho\sigma^2 + \frac{1-\rho}{B}\sigma^2\tag{1}\]가 된다. Bootstrap 개수인 $B$가 증가할수록 두번째 항은 무의미해지지만, 첫번째 항이 남아있고 이는 트리 간 상관계수가 평균화averaging로부터의 이득을 감소시킨다는 것을 의미한다. 결국 RandomForest의 핵심은 bagged treee들의 상관관계를 줄이는 것이고, 이를 통해 평균값의 분산을 감소시키는 것이다. 이는 위 알고리즘에서, 예측변수들의 random selection 과정을 통해 해결할 수 있다. 즉,
Tree를 split하는 각 단계들 이전에 $m\leq p$ 개의 Input variable들을 랜덤으로 선택하고(candidates) 이들 중에서 split할 variable을 정한다.
위와 같은 과정을 통해 random selection을 실행할 수 있고, 일반적으로 $m$값은 $\sqrt p$의 값을 쓰는데, $1$처럼 낮은 값을 갖는 경우도 있다. 각 Tree에 대해 split variable과 split point를 parameter $\theta_b$ 로 표현하면 Random Forest algorithm을 통해 생성한 트리의 열을 \(\lbrace T(x:\theta_b\rbrace _1^B\) 로 표기할 수 있고, 새로운 데이터에 대한 예측값을
\[\hat f^B(x) = {1\over B}\sum_{b=1}^B T(x:\theta_b)\]와 같이 나타낼 수 있다. 이렇게 만들어지는 Random Forest 모델은 튜닝해야할 hyperparmeter의 수가 적은 동시에 괜찮은 성능을 낸다고 알려져있다. 특히, 앞서 언급한 parmeter $m\leq p$ 의 경우 분류 모델에서는 $\sqrt p$를, 회귀 모델에서는 $p/3$ 을 각각 기본값으로 설정하는 것이 일반적이다.
Details of Random Forest
Out-of-Bag Samples
랜덤포레스트 모형의 중요한 특징 중 하나로 out-of-bag(OOB) 샘플을 사용한다는 것이다. 여기서 out-of-bag이란, 배깅(bag) 과정에서 사용되지 않은 샘플을 의미하는데 랜덤포레스트의 경우 배깅을 통해 생성된 트리들 모두에 포함되지 않은 관측값들을 의미한다. 역으로, 애초에 random forest predictor model을 구현할 때 어떤 관측치 $z_i=(x_i,y_i)$ 에 대한 예측값을 구하고자 한다면 $z_i$를 포함하지 않는 bootstrap sample들로 모델을 만드는 것이다. 이렇게 만든 모델의 error를 OOB error라고 정의한다.
Variable Importance
Random Forest 모델의 경우 GBM의 Variable Importance(Influence)를 측정하는 것과 유사하게 각 변수의 중요도를 측정할 수 있다. 개별 트리의 각 split 과정에서 일어나는 각 split-criterion의 개선 정도는 Importance의 측도로 여겨지고 이는 트리 전체에 걸쳐서 계산된다. 이때, 앞서 언급한 OOB sample을 이용해 Variance Importance를 계산할 수 있는데, $b$번째 트리를 만듦과 동시에 OOB sample을 해당 모델에 통과시켜 예측의 정확도를 계산한다. 이후 $j$번째 변수(splitting variable)의 값을 임의로 변화시켜 정확도의 감소치를 측정할 수 있는데, 랜덤포레스트의 모든 트리에 걸쳐 이러한 감소치의 평균치를 측정하면 이를 $j$번째 변수의 중요도로 사용할 수 있다.
Analysis of Random Forests
이제 Random Forest 모델에서의 추가적인 randomization 메커니즘을 다루어보도록 하자. 여기서는 설명의 편의를 위해 Regression 문제와 Squared Loss에 대해서만 다루고, 분류 문제나 0-1 Loss에 대해서는 생략하도록 하겠다.
Bias-Variance Tradeoff
랜덤포레스트 모델의 Bagging size(Bootstrap size) $B$를 무한히 크게하는 상황을 생각해보자. 그러면 랜덤포레스트 모형의 예측값 $\hat f(x)$는 근사적으로 개별 트리의 output에 대한 기댓값으로 수렴하게 될 것이고, 이는 대수의 정리LLN, Law of Large Numbers으로부터 유추할 수 있다. 즉,
\[\lim_{B\to \infty}\hat f(x)_{\text{rf}}^B = \text{E}_\theta T(x:\theta)\]의 관계가 성립한다. 이때, parameter $\theta$는 사실상 training data $Z$에 의존하므로, 이를 명시적으로 다음과 같이 표시할 수 있다.
\[\hat f_{\text{rf}}(x) = \text{E}_{\theta\vert Z}T(x:\theta(Z))\;\;\text{as}\;\; B\uparrow\infty\]또한, 여기서는 한 점(single target point) $x$에 대한 추정치만 고려하도록 하자. 그러면 앞선 식 (1)로부터
\[\text{Var}\hat f_{\text{rf}}(x) = \rho(x)\sigma^2(x)\]가 성립하는데, 여기서 $\rho(x)$ 는 랜덤포레스트의 임의의 두 트리에 대한 표본상관계수이다. 즉,
\[\rho(x) = \text{corr}[T(x:\theta_1(Z)),T(x:\theta_2(Z))]\tag{2}\]이고 여기서 $\theta_1(Z),\theta_2(Z)$ 는 임의의 샘플 $Z$에 대한 랜덤포레스트에서 임의로 추출한 두 트리를(parameter) 의미한다. 또한, $\sigma^2(x)$ 는 sampling variance로, 임의의 개별 트리에 대한 분산
\[\sigma^2(x)=\text{Var}(T(x:\theta(Z)))\]를 의미한다. 이때 주의해야 할 것은, $\rho(x)$가 이미 주어진 random forest ensemble에 대한 표본상관계수가 아니라는 점이다. $\rho$는 임의의 샘플에 대한 상관계수이므로, 이론적인(theoretical) 상관계수라고 보는 것이 더 적절하다. 통계학적으로는, 이는 training data $Z$와 $\theta$의 sampling distribution표본분포로부터의 상관관계를 의미하는 것이다. 즉 식 (2)에서의 variability는 각 split 단계에서의 sampling으로 인해 $Z$에 종속적일 뿐 아니라, $Z$를 sampling하는 것에서의 variability도 포함한다.
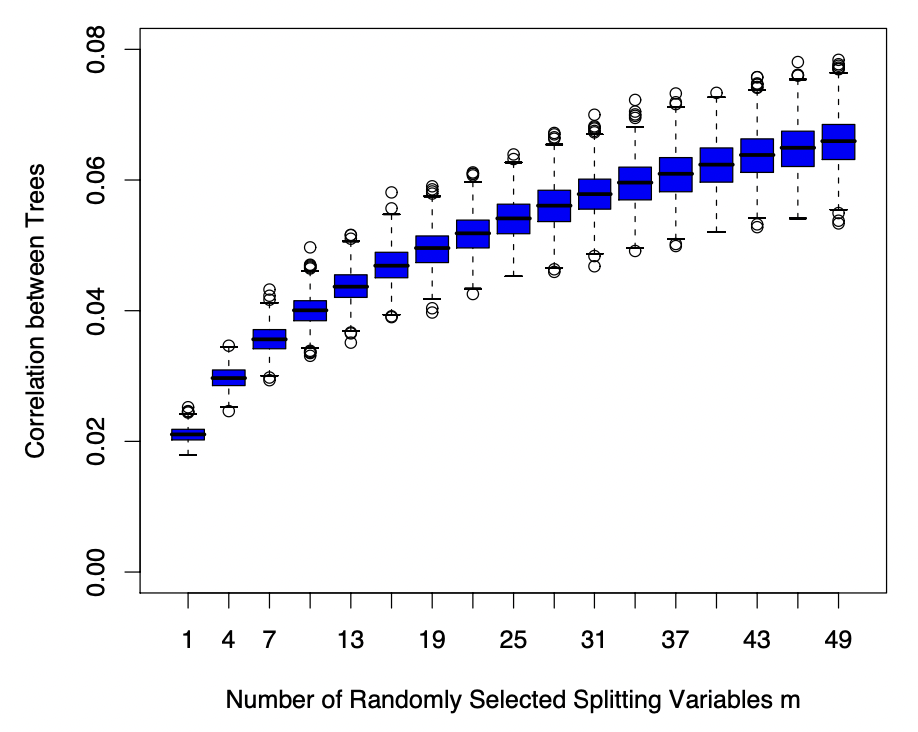
위 plot은 식 (2)의 correlation이 splitting variable의 개수와 어떤 관련이 있는지를 나타낸다. 즉, 같은 splitting variable을 사용하는 트리 간에는 예측 값 간에 유사성이 발생할 가능성이 높으므로, 변수 개수가 증가하면 그에 따라 트리 간의 correlation 역시 증가하게 된다. 반면, 개별 트리에 대한 분산의 경우 다음과 같이
\[\text{Var}_{\theta, Z}T(x:\theta(Z)) = \text{Var}_Z(\text{E}_{\theta}[T(x:\theta(Z)\vert Z)])+\text{E}_Z[\text{Var}_\theta(T(x:\theta(Z)\vert Z))]\]로 분리될 수 있는데(이중기댓값 정리), 여기서 우변의 첫째 항은 randomforest 모형의 sampling variance 이고, 이는 splitting variable의 size $m$에 의해 크게 변하지 않는다. 다만 둘째 항은 randomization에 의해 발생하는 within-$Z$ Variance 인데, 이는 randomization에 관련된 요소 $m$의 크기가 커질수록 증가하게 되어 전체 Variance를 증가시킨다. 결국 여기서도 Bias-Variance Tradeoff가 발생하게 되며, splitting variable의 개수를 최적화해야하는 문제가 발생한다.
References
- The Hastie, T., Tibshirani, R., Friedman, J. H., & Friedman, J. H. (2009). The elements of statistical learning: data mining, inference, and prediction (Vol. 2, pp. 1-758). New York: springer.
Leave a comment