Robust PCA

Background

Robust PCA는 Principal component analysis가 그 이름에 포함되어 있지만, 본질적으로 접근 방식이 일반적인 PCA와는 사뭇 다르다. PCA는 일반적으로 특이값분해(SVD)를 이용해 분산을 최대화하는 고유벡터와 그것에 대한 projection을 구하는 방식이다. 다만, PCA의 경우 이상치에 대해 매우 민감한데, 아래 그림처럼 일부의 이상치(빨간색 데이터)에 대해 주성분 벡터가 상당히 변화할 수 있다.

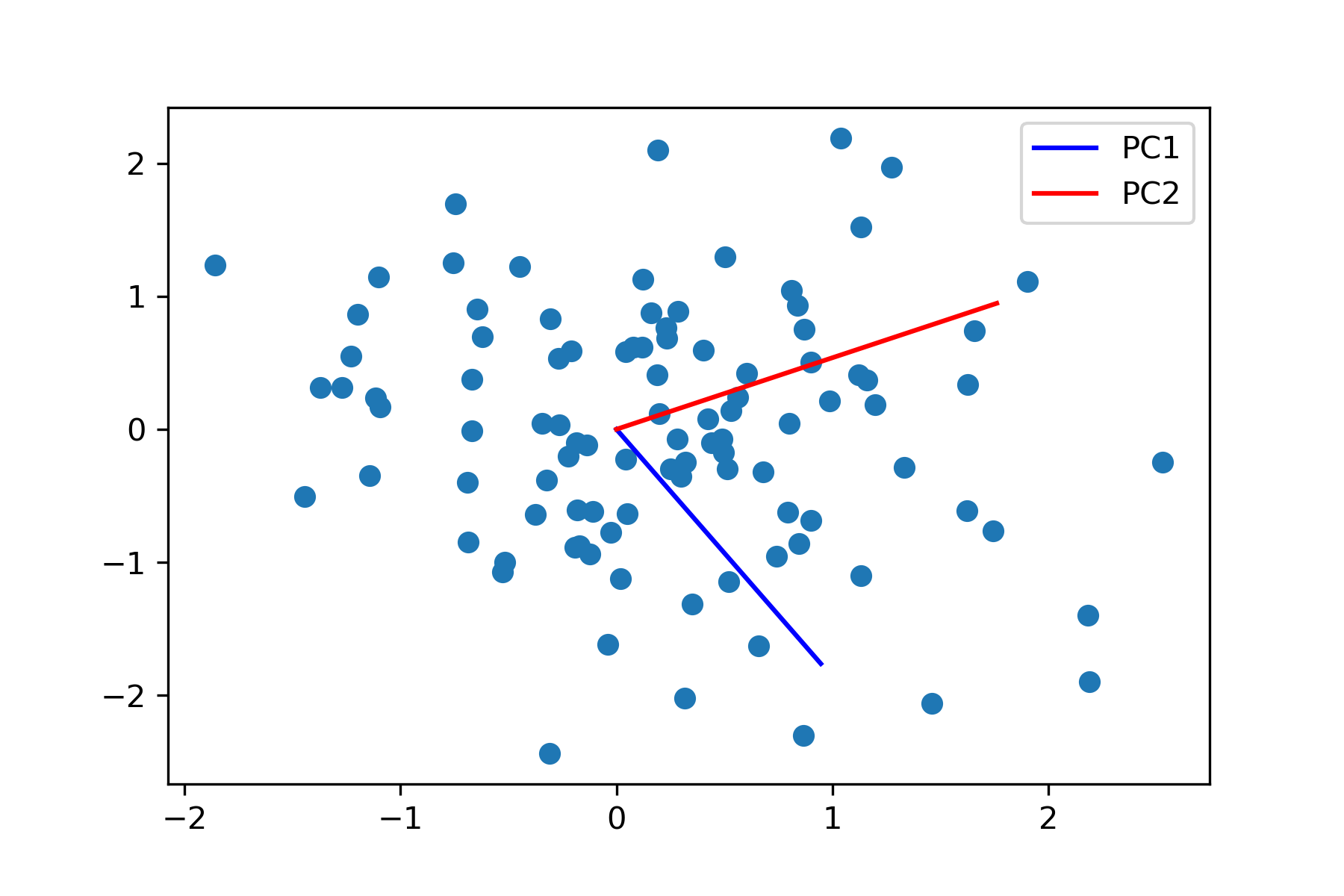
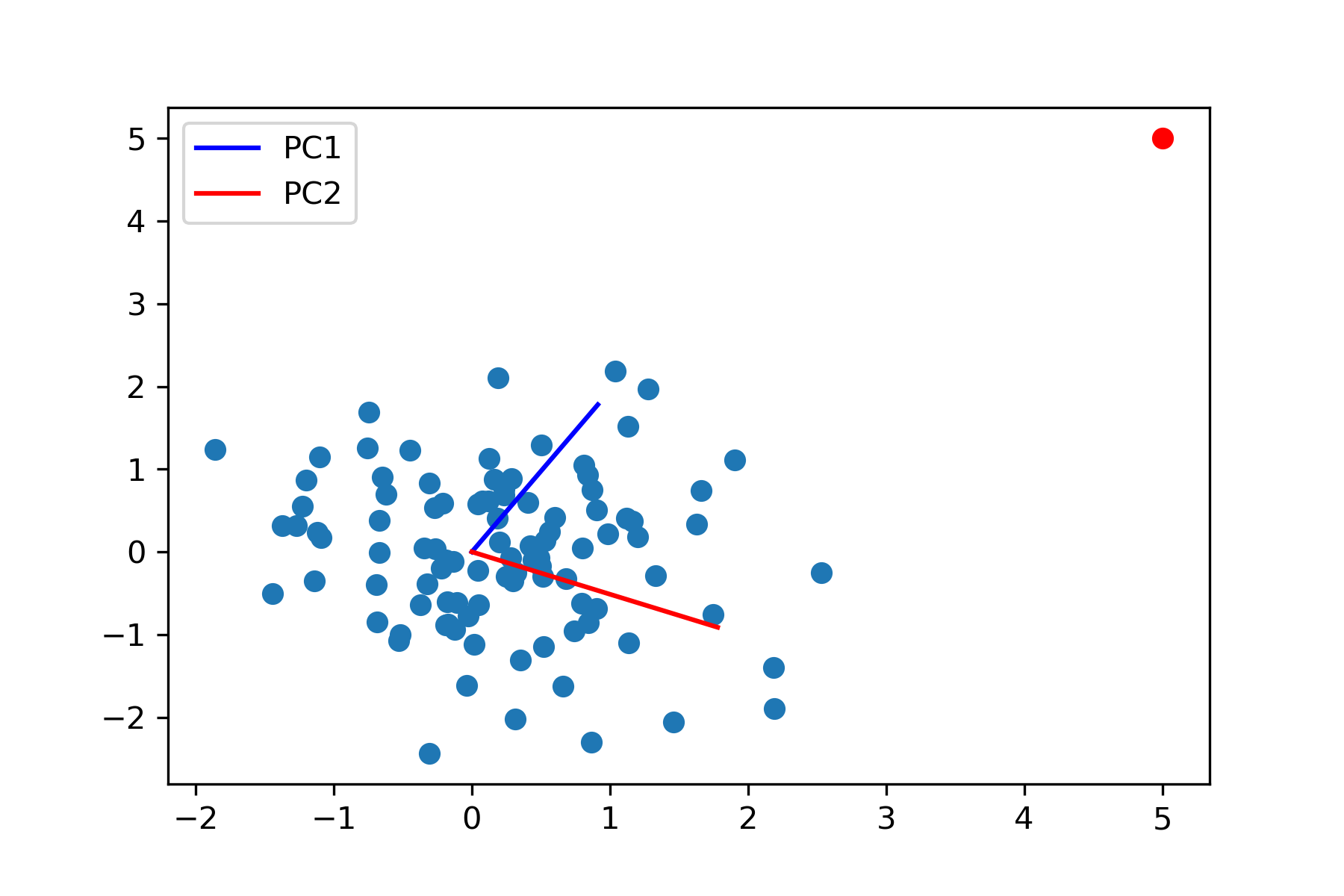이상치가 있는 경우(빨간색 점)

Robust PCA는 이러한 PCA의 non-robustness를 보완하는 방법이지만, 근본적으로 살펴보면 다음과 같은 행렬 분해를 추정하는 기법이다.

\[M = L + S\]

여기서 $M$은 주어진 데이터 행렬을 의미하며, $L$은 low-rank matrix, $S$는 Sparse matrix를 의미한다. Low-rank, Sparse matrix는 각각 다음과 같이 이해하면 편리하다. (구체적인 내용은 아래 Experiment 참고)

Example. CCTV 영상 자료 = 배경 + 동체

예를 들어 CCTV 영상 데이터가 주어졌다고 하자. 그렇다면 해당 영상을 프레임별로 추출하면 각 프레임은 2-dimensional matrix로 주어진다(RGB채널은 고려하지 않고 흑백 영상으로 주어졌다고 하자). 그러면, 각 프레임을 column, 프레임별 데이터를 row로 하는 $N\times f$ 데이터를 생각할 수 있다. 이 경우에 대해 robust PCA를 실시하게 되면 Low-rank matrix로는 해당 영상의 배경(움직이는 물체를 제외한)을 얻을 수 있고, sparse matrix로는 움직이는 물체, 사람 등을 추출할 수 있다. 이러한 아이디어로, robust PCA는 배경 추출, 얼굴 인식 등의 기술적인 활용도 이루어진다.

Theory

Robust PCA는 앞서 언급한 Low rank matrix $L$과 Sparse matrix $S$를 동시에 추정해야 하는데, Chandrasekaran et al.(2011) 에 따르면 두 행렬을 추정하는 것을 다음과 같은 최적화 문제로 변환할 수 있다.

\[\min_{\mathbf{L,S}} \Vert L\Vert_{\ast}+\Vert S \Vert_{1}\quad \mathrm{s.t. } \;\;\mathbf{Y=L+S}\]

여기서 각 노음 $\Vert\cdot\Vert_{\ast}$ 및 $\Vert\cdot\Vert_{1}$ 은 각각 Schatten 1-norm(특이값들의 합), 1-norm(모든 원소들의 절댓값들의 합)으로 정의된다. 위 최적화 문제를 푸는 알고리즘에는 여러 종류가 제안되었는데, 여기서는 Manifold Optimization을 이용한 알고리즘을 다루어보고자 한다.

MorPCA

엄밀히 하자면, Manifold optimization이 이용되는 과정은 최적화 과정 중 Gradient Descent 알고리즘 과정에서 이루어진다. Manifold optimization을 이용한 gradient descent는 여러 이전 논문에서 제안되었는데(Vandereycken(2013) 등), 다음과 같은 원리로 이루어진다.

우선 smooth manifold(Riemmanian) $\mathcal{M}\subset\mathbb{R}^{n}$ 과 미분가능한 함수 $f:\mathcal{M}\to \mathbb{R}$ 을 고려하자. 이때 최적화 문제

\[\min_{x\in\mathcal{M}} f(x)\]

를 푸는 알고리즘은 다음 단계들로 구성된다.

  1. 함수 $f$를 $\mathbb{R}^{n}$ 에서 정의되었다고 생각하고, Euclidean gradient

    \[\nabla f(x)\]

    를 구한다.

  2. Riemmanian gradient를 구하는데, 그래디언트의 방향은 tangent space $T_{x}\mathcal{M}$ 에서 나타나는 $f(x)$의 steepest ascent으로 주어진다. 즉, 이 방향은 projection operator

    \[P_{T_{x}\mathcal{M}}\]

    으로 주어진다.

  3. Tangent space에서 manifold로 다시 매핑하는 Retraction $R_{x}$를 다음과 같이 정의한다.

    \[\begin{aligned} &R_{x}:T_{x}\mathcal{M}\to \mathcal{M}\quad \mathrm{where}\\ &R_{x}(0)= x\\ &R_{x}(y)= x+y+O(\Vert y\Vert^{2})\;\mathrm{as}\; y\to 0 \end{aligned}\]

  4. Gradient Descent algorithm의 업데이트는 다음과 같이 주어진다.

    \[x^{\mathrm{new}}=R_{x}(-\eta P_{T_{x}\mathcal{M}}\nabla f(x))\]

Experiment

Data

실제 CCTV video 데이터(VIRAT Dataset)에 대해 MorPCA 알고리즘을 적용하여 배경추출을 해보았다. 영상의 크기는 720*1280 이며, 계산비용 절감을 위해 해상도를 10분의 1로 낮추어 각 프레임이 72*108 크기의 이미지를 갖도록 설정하였다(SVD 과정에서 계산비용이 과도해지는 문제 발생). 또한, 프레임 역시 전체 584프레임 중 59프레임만 이용하였다.

Algorithm

MorPCA 알고리즘은 Riemmanian optimization 과정에서 projective/orthographic retraction의 두 가지 방법을 사용가능하도록 되어있는데, 여기서는 orthographic 알고리즘을 사용하였다. 또한, 일부 튜닝 파라미터들은 논문에서와 마찬가지로 다음과 같이 설정하였다.

\[\begin{aligned} r &= 3\;:\;\text{rank of low-rank approximation } \mathbf{L}\\ \gamma&= 0.1\;:\;\text{Percentile for hard thresholding} \end{aligned}\]

Gradient descent 알고리즘은 총 반복횟수를 100회로 지정하였으며(maxiter), 예시 결과는 다음과 같다.

위 두 사진은 첫 번째 프레임 이미지에 대한 처리 전/후 사진을, 아래 두 사진은 25번째 프레임에 대한 처리 전/후 사진을 나타낸다. 각 처리 후 사진은 low-rank approximation $\mathbf{L}$의 각 프레임에 해당하는 열벡터를 이미지로 재구성한 것인데, 배경 추출이 잘 이루어졌음을 확인할 수 있다.

전체 코드는 아래 Github repository를 참고하면 된다.

References

Leave a comment