SOM 이라고 줄여 부르는 Self-organizing maps는 고차원(High dimensional) 데이터를 저차원(주로 2차원 평면)에 표현하는 차원축소 기법의 일종이다. 차원축소 기법으로 많이 사용되는 PCA와는 다르게, SOM은 데이터의 고차원 구조(topological structure)를 보존하여 Feature space에 embedded된 2D manifold(다양체)로 표현한다. SOM의 알고리즘을 간단하게 이해하면, 2차원 평면을 고차원 데이터에 적합시키기 위해 해당 평면을 휘거나, 구부리는 등의 2차원 manifold로 바꾼다고 생각하면 된다(아래 그림).

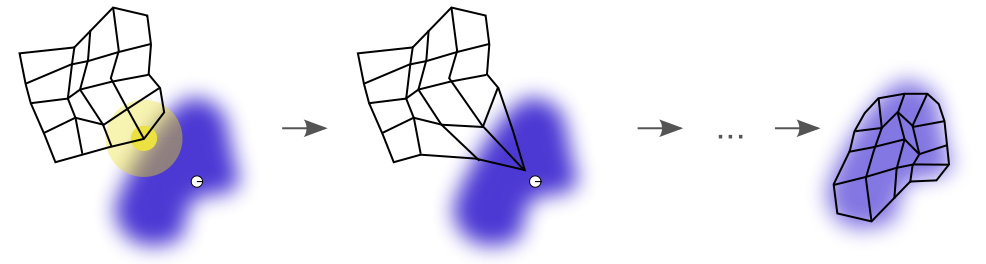출처 : https://en.wikipedia.org/wiki/Self-organizing_map

High-dimensional data $X_{i}\in \mathbb{R}^{p}$ 가 주어진다고 하자. 일반적으로 데이터의 시각화를 위해 2차원 격자가 자주 사용되며, 격자의 가로, 세로 크기가 각각 $q_{1}, q_{2}$ 라면 각 격자를 prototype $m_{j}\in \mathbb{R}^{p}, j\in \lbrace 1,\ldots, q_{1}\rbrace \times \lbrace 1,\ldots,q_{2}\rbrace $ 라고 한다. 각 prototype이 2차원 벡터가 아니라 $p$차원 벡터인 이유는, PCA 처럼 기존 고차원 데이터를 저차원(ex. 주성분)에 직접 projection하지 않고, 각 prototype과 기존 데이터의 Euclidean distance를 구하는 과정으로 projection시키기 때문이다. 따라서, projection이라는 개념보다 각 prototype이 자신과 가장 가까운 데이터들을 포함시킨다는 의미에서 오히려 clustering의 개념이 더 적절하다.

Algorithm

SOM Algorithm의 대략적인 진행 과정은 다음과 같다.

  1. Prototype vectors $m_{j}\in \mathbb{R}^{p}$ 을 초기화한다
  2. 각 prototype $m_{j}$에 대해 Euclidean distance가 가장 가까운 데이터 $X_{i}$를 찾는다. (이를 best matching unit, BMU 라고 한다.
  3. BMU를 바탕으로 Prototype vector를 업데이트한다.
\[m_{j}^{NEW} \leftarrow m_{j}+ \alpha(X_{i}-m_{j})\]

이때 1번의 초기화 과정은 SOM을 처음 제안한 Kohonen의 경우 Random initialization(Stochastic initialization)을 이용했다($\mathbb{R}^{p}$ 에서 랜덤하게 선택). 다만 최근에는 정확한 알고리즘을 위해 initial vector를 first principal component 공간으로부터 random하게 선택하는 방법을 사용하고 있다. 이를 Principal component initialization이라고 한다.

다만, 데이터셋이 nonlinear한 경우, PCA 자체가 데이터셋의 nonlinear structure를 잘 파악하지 못하기 때문에, random initialization이 더 낫다는 연구 결과가 있다(“SOM: Stochastic initialization versus principal components”).

Example

MNIST 손글씨 데이터를 활용해 숫자 0, 1, 2에 해당하는 데이터들을 SOM으로 분류해보았다. minisom 패키지를 활용했으며, MiniSom 함수를 이용해 다음과 같이 알고리즘을 설정할 수 있다.

# SOM
som = MiniSom(x=10, y=10, input_len=784, sigma=1.0, learning_rate=0.5)
som.random_weights_init(X_train)
som.train_random(data=X_train, num_iteration=100)

총 $10\times 10$ Grid를 이용했으며, 분류 결과는 다음과 같다.

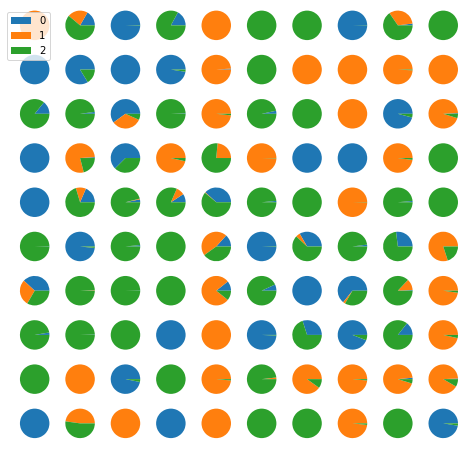
각 동그라미는 prototype을 나타내며, 해당 Prototype에 가까운 데이터들이 어떤 비율로 구성되어있는지 개별 파이형 도표로 나타냈다. 실제로 분류 결과를 살펴보면 97% 정도의 정확성을 보였다. 코드는 다음과 같다.

# Accuracy for test data
# Predict
y_pred = []
for i in range(len(X_test)):
    # winner
    w = som.winner(X_test[i])
    # label
    counter = labels_map[w]
    y_pred.append(max(counter, key=counter.get))

# Confusion matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
print(cm)

# Accuracy
from sklearn.metrics import accuracy_score
accuracy_score(y_test, y_pred)

# 0.9733079122974261

반면, PCA를 이용하여 KNN classifier로 분석한 결과는 다음과 같다. 우선 PCA plot(아래)로부터 알 수 있듯이, 단순히 두 개의 주성분에 대해 linear projection하는 것만으로는 784차원의 기존 데이터를 잘 분리해낼 수 없다.

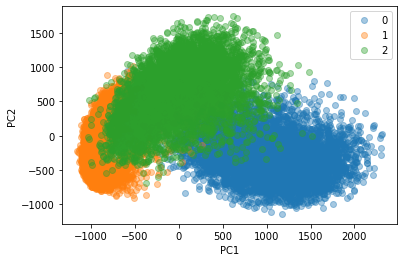
5-NN Classifier을 이용해 clustering을 실시한 결과 정확도가 더 낮음을 확인할 수 있었다.

# KNN with PCA
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X_pca[:, :2], y_train)
y_pred = knn.predict(pca.transform(X_test))

# Accuracy
accuracy_score(y_test, y_pred)

# 0.9428026692087702

References

  • Wikipedia : https://en.wikipedia.org/wiki/Self-organizing_map
  • KOCW Manifold Learning 김충락 교수님 강의(현대통계학특강)
  • Code on Github : https://github.com/ddangchani/Velog/blob/main/Statistical%20Learning/Self%20Organizing%20map.ipynb

Leave a comment