Splines

Splines

Spline^스플라인은 데이터셋을 부분적으로 나누어 각 부분에 대해 다항식을 적합하는 방법입니다. 추정하고자 하는 회귀모형이 비선형적인 형태를 가지고 있을 때, 이를 선형모형으로 근사하는 방법 중 하나입니다. 이는 기저확장^{basis expansion}의 한 형태로 볼 수 있습니다. 이번 글에서는 B-spline을 중심으로 spline의 구성요소와 이를 이용한 회귀모형을 살펴보겠습니다.

Basis Expansion

기저 확장이란 데이터셋 $\mathbf{X}$의 각 벡터 $X\in\mathbf{X}$에 새로운 변수를 추가하거나, 기존 변수를 대체하는 방법으로 새로운 모형을 구성하는 것이다. 총 M개의 변환이 존재한다고 하고, 이때 $m$번째 ($m= 1,\ldots,M$) 변환을

\[h_m(X) : \mathbb{R^p\to R}\]

로 표기하자(기존 데이터는 p개의 변수를 가지고 있음). 이를 이용해 생성한 새로운 선형 모델

\[f(X) = \sum_{m=1}^M\beta_m h_m(X)\]

을 $\mathbf{X}$에서의 선형 기저확장^{linear basis expansioon} 이라고 한다. 회귀분석에서 다루는 여러 스킬들 역시 기저확장의 관점으로 접근가능하다. 만일 $h_m(X) = X_m$이면 $f(X)$는 기존 선형모델과 동일하다. 만일 $h_m(X) = X_j^2$ 이나 $h_m(X) = X_jX_k$ 형태의 변환이 주어지면 이는 이차항을 추가한 선형회귀모형(또는 quadratic model)이 된다.

B-splines

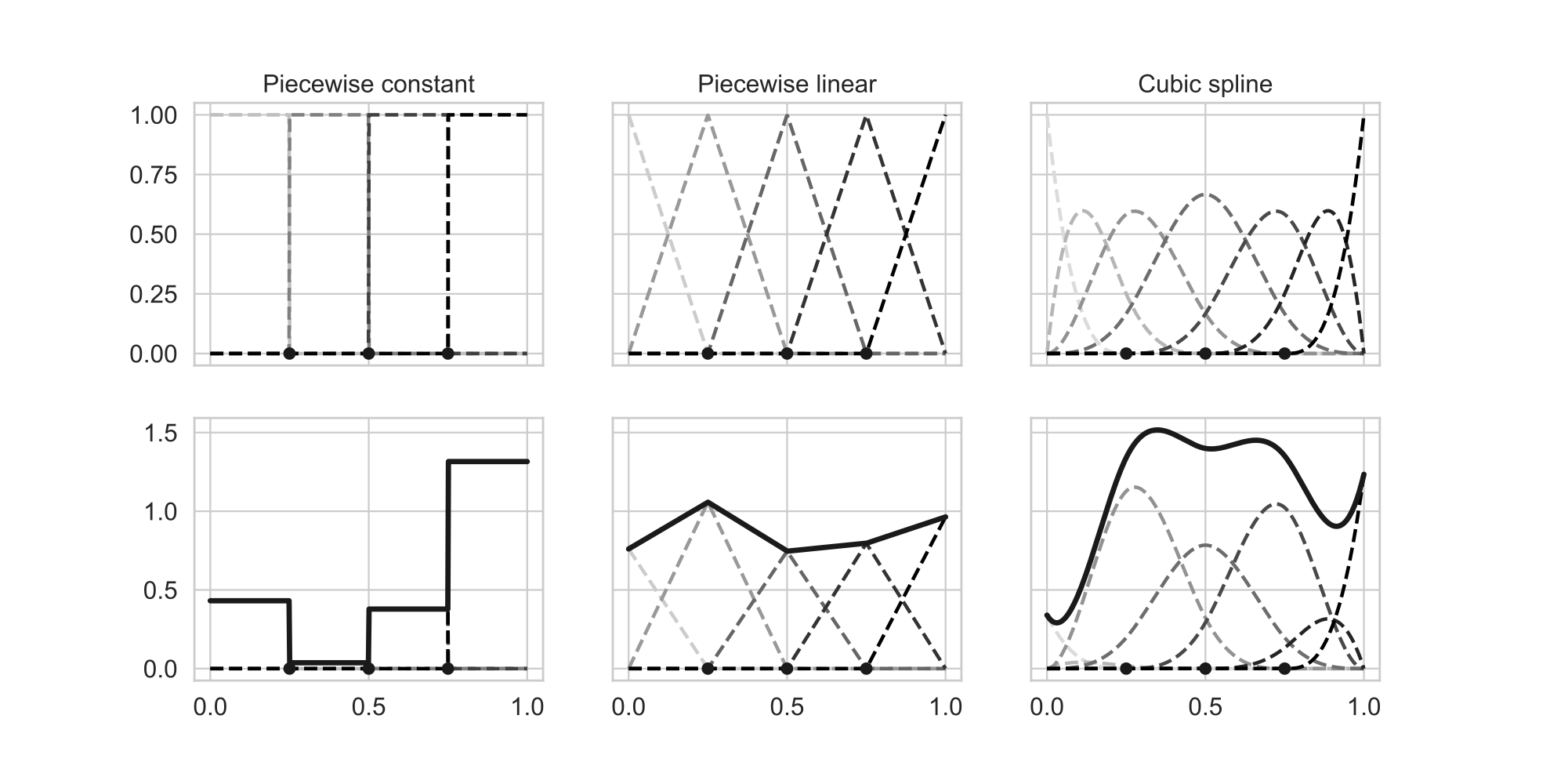B-splines (source: Murphy, 2022)

기저함수 $h(x)$를 구성하는 가장 일반적인 방법은 B-spline을 사용하는 것이다 (위 그림 참고). 여기서 B는 basis를 의미하며, 스플라인 기법은 $X$의 정의역^domain을 여러 부분으로 나누어 해당 부분에 대한 회귀모델을 구현하는 것이다. 정의역을 여러 부분으로 나누기 때문에, 각 부분이 나누어지는 지점을 매듭^knot이라고 부른다. 각 부분(piece)에 대한 회귀모델은 다항식으로 주어진다. 각 부분을 상수함수로 주는 경우 piecewise constant라고 하고, 선형함수로 주는 경우 piecewise linear라고 한다.

여기서는 설명의 편의를 위해 $X$의 차원은 일차원으로 주어지고, 정의역을 세 부분으로 나누는 상황을 생각해보자.

Piecewise constant

제일 먼저 가장 단순한 형태로 주어지는 기저함수를 생각하자. $X$의 정의역이

\[[\inf X,\xi_1),[\xi_1,\xi_2),[\xi_2,\sup X]\]

의 세 부분으로 나누어진다고 하자. 이때 다음과 같이 세 개의 basis function이 주어지는 상황을 생각하자. (상수가 곱해지지 않고 지시함수로 주어진다.)

\[\begin{aligned} h_1(X)&=I(X<\xi_1) \\ h_2(X)&=I(\xi_1\leq X<\xi_2) \\ h_3(X)&=I(\xi_2\leq X) \end{aligned}\]

그러면 모델은

\[f(X)=\sum_{m=1}^3\beta_mh_m(X)\]

꼴이 되어 총 세 개의 회귀계수를 추정해야 하고, 이때 각 계수는 각 영역에서 $Y$의 평균으로 주어진다. 또한, 부분별로 회귀식이 상수항으로 주어지므로 이를 piecewise constant 모델이라고 한다 (위 그림의 왼쪽). Step function이라고도 불린다.

Piecewise linear

만일 앞선 세 개의 basis functions에 추가로 세 개의 basis function

\[h_{m+3}=X\cdot h_m(X)\quad m=1,2,3\]

을 추가하면 이는 각 부분에서 선형인 모델이 되고 이를 piecewise linear라고 한다 (아래 그림 참고).

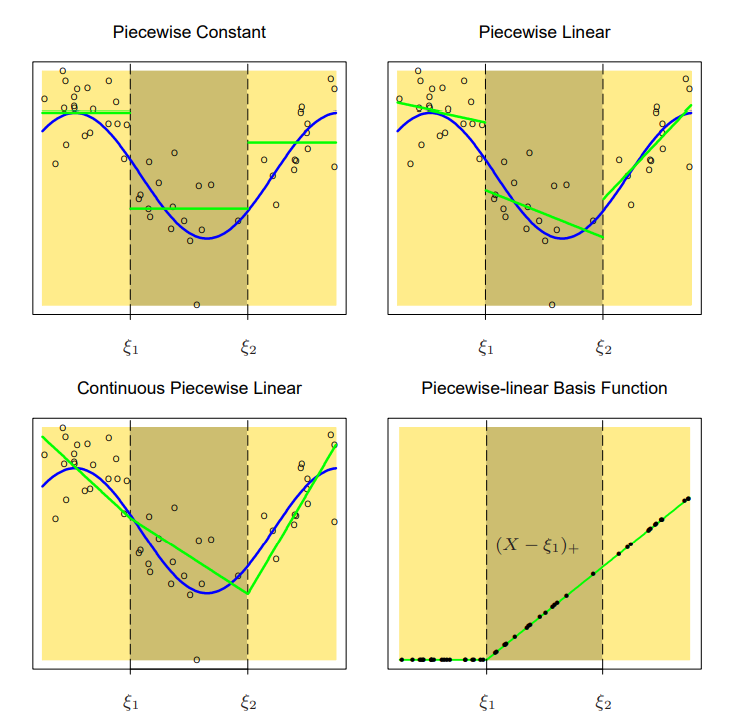Piecewise Constant and Linear (source: Elements of Statistical Learning)

그런데 위 그림에서 볼 수 있듯 제약조건을 걸지 않으면 선형 모형이 각 spline에서 불연속적이고, 이는 모델 추정의 효용을 감소시킨다. 따라서 연속적이어야 한다는 제약조건

\[f(\xi_1^-)=f(\xi_1^+)\]

을 추가하면 $\beta_1+\xi_1\beta_4=\beta_2+\xi_1\beta_5$ 라는 제약조건이 되고, 결과적으로 추정해야할 모수는 4개가 된다. 이를 간단하게 쓰면,

\[h_1(X)=1,\;\;h_2(X)=X,\;\;h_3(X)=(X-\xi_1)_+,\;\;h_4(X)=(X-\xi_2)_+\]

의 basis function 4개로 표현가능하다.

Piecewise Polynominal

위의 메커니즘을 이용하면, 각 piece에 대해 다항모델을 설정하고 다양한 제약조건을 부여할 수 있다. 앞선 제약조건처럼 경계점에서 연속이 되는 조건 뿐 아니라, 경계점에서 도함수^derivative 혹은 이계도함수가 연속인 조건을 부여하여 모형을 좀 더 smooth하게끔 만들어줄 수 있다. 만일 삼차다항모형에서 이계도함수가 연속인 spline을 생각한다면(cubic spline), 총 여섯 개의 basis로 이를 표현할 수 있다. (3개의 구역 * 구역당 4개의 모수 - 2개의 경계점 * 경계당 3개의 제약조건 = 6)

일반적으로 각 구역이 $M-1$차 다항식($M$개의 parameter)으로 정의되고 각 매듭^knots(각 구역의 함수들이 만나는 지점) $\xi_j,\;\;j=1,\ldots,K$ 에서 $M-2$ 차 도함수가 연속인 경우를 $M$차 spline이라고 정의한다. 바로 위에서 말한 cubic spline은 $M=4$ 인 경우이다 (3차다항식 + 2차도함수의 연속). 이를 일반화하면

\[\begin{aligned} h_j(X)&=X^{j-1}\quad j=1,\ldots,M\\ h_{M+l}(X)&=(X-\xi_l)^{M-1}_+\quad l=1,\ldots,K \end{aligned}\]

으로 order-$M$ spline을 나타낼 수 있다.

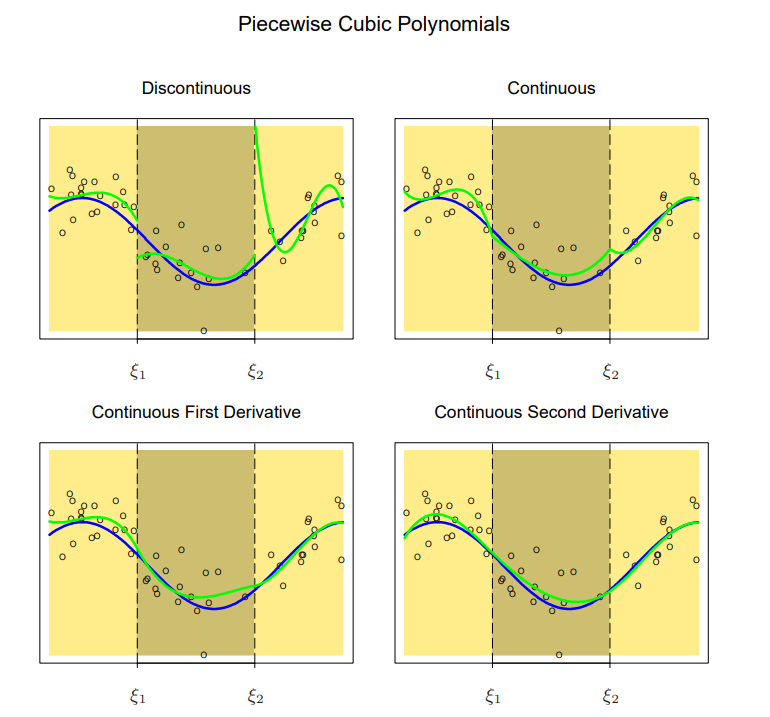Piecewise Cubic Spline (source: Elements of Statistical Learning)

위 그림에서 볼 수 있듯이, 도함수의 연속성을 부여할수록 모델은 더 smooth해지게 된다.

Smoothing Splines

​앞서 spline을 구성하는 방법들에 대해 살펴보았는데, spline에서 사용되는 매듭의 개수는 어떻게 정해야 하는지에 대해 다루어보도록 하자. 간단히 생각해보면, 매듭의 개수를 늘릴수록 모델을 데이터에 근접하게 만들 수 있을 것이고, 그에 따른 복잡성(분산) 역시 증가할 것이다.

즉, 매듭의 개수 역시 bias-variance trade-off의 관계선상에 있으므로 특정 방법을 이용해 일종의 hyperparameter로서 규제하는 것이 필요하다. 우선, 다음과 같은 trade-off regularization을 살펴보자.

\[\text{RSS}(f,\lambda)=\sum_{i=1}^N\lbrace y_i-f(x_i)\rbrace ^2+\lambda\int\lbrace f''(t)\rbrace ^2dt\tag{1}\]

이계도함수가 존재하는 함수 $f$ 중 위 식 1을 최소화하는 함수를 찾는 상황을 생각해보자. 식 1에서 첫번째 항은 데이터셋에 해당 함수가 어느정도 가까운지, 즉 편향을 측정해주는 항이다. 반면 두번째 항은 곡률^curvature을 측정하는 것으로, 패널티 항으로 작용하고 $\lambda$를 통해 규제의 강도를 조절한다.

쉽게 생각하기 위해 $\lambda=0$ 인 경우와 $\lambda=\infty$ 인 경우를 살펴보면, 먼저 $\lambda=0$ 인 경우에는 규제가 이루어지고 있지 않으므로 모든 데이터 점을 지나는 임의의 함수가 된다. 반면, $\lambda$를 크게 할수록 이계도함수가 0이 아닌 값을 갖게되면 발산하게 되므로 함수 $f$는 선형함수에 가까워지고 이는 최소제곱법을 의미한다.

Natural cubic spline

식 (1)의 규제를 만족하는 함수는 explicit한 형태로 구해지며, 그 형태는 Natural cubic spline 이라는 형태의 spline이며, spline의 각 매듭은 각 데이터 $x_i,\;\;i=1,\ldots,N$ 으로 주어진다. Natural cubic spline은 polynominal spline에서 추가적인 규제를 더하는데, polynominal spline의 각 경계점(매듭)인근에서 linear한 형태를 갖게끔 한다.

이를 통해 모델의 자유도를 낮추고, bias-variance trade-off를 조절한다. Piecewise Polynominal에서 살펴본 일반화된 Polynominal spline의 각 basis function $h_k(X)$들은 다음과 같이 변환된다.

\[\begin{aligned} N_1(X)&=1 \\ N_2(X)&=X \\ \vdots \\ N_{k+2}(X)&=d_k(X)-d_{K-1}(X) \end{aligned}\]

여기서

\[d_k(X)=\frac{(X-\xi_k)^3_+-(X-\xi_K)^3_+}{\xi_K-\xi_k}\]

으로 주어진다. 이때 각 basis function $N_k$ 들은 $X\geq\xi_K$에서 이계도함수가 0임을 확인할 수 있다.

식 (1)의 해 $f$는 $N$개의 basis function으로 나타나며, 그 형태는

\[f(x)=\sum_{j=1}^NN_j(x)\theta_j\]

과 같다. 이때 $\lbrace N_j:j=1,\ldots,N\rbrace $​ 은 $N$ 개의 natural cubic spline 기저함수들의 집합이다. 이를 이용해 식 (1)을 Linear Form으로 표기하면

\[\text{RSS}(\theta,\lambda)=\mathbf{(y-N\theta)^\top(y-N\theta)+\lambda\theta^\top\Omega_N\theta}\tag{2}\]

이때 행렬 $\mathbf{N}$은 $\lbrace \mathbf{N}\rbrace _{ij}=N_j(x_i)$​으로 주어지고 행렬 $\mathbf{\Omega}$ 는

\[\lbrace \mathbf{\Omega}_N\rbrace _{jk}=\int N''_j(t)N''_k(t)dt\]

으로 정의된다. 식 (2)의 해를 구하면

\[\hat{\theta}=(\mathbf{N^\top N+\lambda\Omega}_N)^{-1}\mathbf{N^\top y}\]

로 주어진다. 이를 이용해 주어지는 다음 함수를 fitted smoothing spline이라고 정의한다.

\[\hat{f}(x)=\sum_{j=1}^NN_j(x)\hat{\theta_j}\]

References

• K. P. Murphy, Probabilistic machine learning: an introduction. in Adaptive computation and machine learning. Cambridge, Massachusetts London, England: The MIT Press, 2022.
• Hastie, T., Tibshirani, R.,, Friedman, J. (2001). The Hastie, T., Tibshirani, R., Friedman, J. H., & Friedman, J. H. (2009). The elements of statistical learning: data mining, inference, and prediction (Vol. 2, pp. 1-758). New York: springer.. New York, NY, USA: Springer New York Inc.