Support Vector Machine

Support Vector Machine

이전에 Linear Classification에서 Fischer’s LDA에 대해 다룬 적 있었다. 이는 특성공간에서 데이터들을 분류하기 위한 선형 경계를 만드는 것인데, support vector classifier/machine은 이와 유사하나 비선형인 결정경계를 만들 수 있다는 점에서 좀 더 일반화된 개념으로 생각하면 된다.

Support Vector Classifier

Hard Margin

$N$개의 observation으로 구성된 데이터셋 $(x_1,y_1),(x_2,y_2),\ldots,(x_N,y_N)$이 주어지고 이때 $x_i\in \mathbb R^p$, $y_i\in\lbrace -1,1\rbrace $ 이라고 하자. 이때 데이터의 분류를 위한 초평면(hyperplane)을 다음과 같이 정의하자.

\[\lbrace x:f(x) = x^T\beta+\beta_0 = 0\rbrace\]

여기서 $\beta$ 는 $\Vert\beta\Vert = 1$ 인 unit vector이며, $f(x)$에 의한 클래스 예측값은

\[G(x) = \text{sgn}(x^T\beta+\beta_0)\]

으로 주어진다. 만일 데이터가 선형경계로 분리될 수 있다고(separable) 가정하면, $y_if(x_i)>0$ 을 만족하는, 즉 실제 클래스와 예측 클래스가 일치하게끔 하는 함수 $f(x)$ 를 찾을 수 있다(아래 그림 참고).

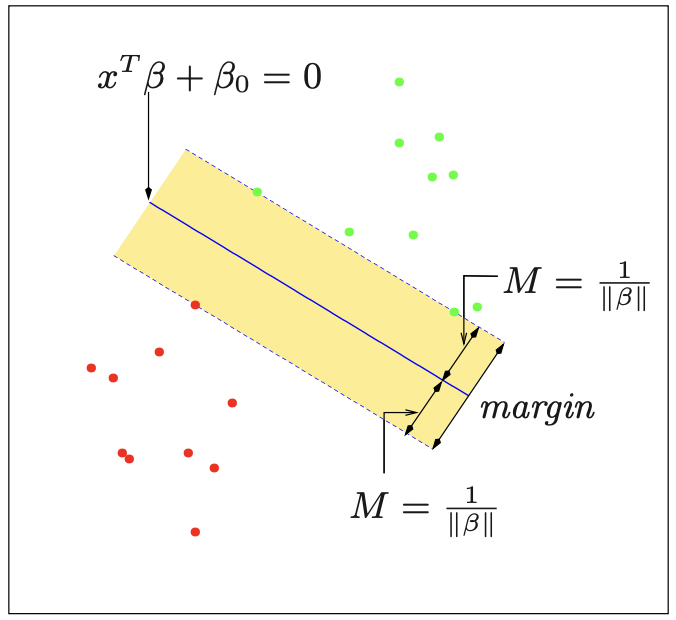
그런데, 이를 만족하는 함수 $f$는 한 개 이상 존재할 수 있으므로, 최적의 classifier을 선택하기 위해서는 다른 기준이 필요하다. 이때 위 그림과 같이 결정경계에서 가장 가까운 데이터들까지의 거리를 margin이라고 정의하면, margin $M$을 최대화하는 최적화문제

\[\max_{\Vert\beta\Vert =1} M\;\;\;\text{subject to}\;\;y_i(x_i^T+\beta_0)\geq M\]

를 만족하는 biggest-margin hyperplane $f$를 찾을 수 있다. 이러한 hyperplane을 만드는 과정은 가장 가까운 데이터들에 의해 결정되므로, 이때 margin 경계에 위치한 데이터들을 support vector라고 정의한다. margin $M$은 hyperplane에서 각 class의 측면으로의 margin을 의미하므로(그림 참고) 전체적인 margin의 너비는 $2M$이라고 볼 수 있다. 만일 노음에 대한 규제 $\Vert M\Vert = 1$ 을 없애면 위 최적화문제를

\[\min_{\beta,\beta_0}\Vert\beta\Vert\;\;\;\text{subject to}\;\;y_i(x_i^T\beta+\beta_0)\geq 1,\;\;i=1,\ldots,N\]

으로 쓸 수 있다. 이때 마진 $M$은 $M=1/\Vert\beta\Vert$ 가 된다. 이처럼 support vector들을 기준으로 클래스의 중첩 없이 hyperplane을 구성하는 모델을 support vector classifier 중에서도 Hard Margin classifier라고도 한다(엄격하게 margin을 지킨다는 의미이다).

Soft Margin

이번에는 특성공간에서 클래스의 중첩이 발생하는 데이터셋을 생각해보자. 즉, 앞선 hard margin classifier을 이용해 데이터를 분류할 수 없고 일부 데이터는 분류기의 반대편(wrong side)에 위치하는 경우를 의미한다. 이를 위해서는 hard margin classifier의 최적화 문제에 완화 변수(slack variable) $\xi=(\xi_1,\xi_2,\ldots,\xi_N),\;\;\xi_i\geq0$ 을 적용하여

\[y_i(x_i^T\beta+\beta_0)\leq M(1-\xi_i),\\ \forall i,\;\xi_i\geq 0,\sum_i\xi_i\leq \text{constant}\]

으로 최적화 문제를 변환할 수 있다. 이렇게 정의한 모델을 support vector classifier의 표준 모델로 사용한다. 여기서 각 완화변수 $\xi_i$는 정량화된 값이라기보단 각 예측치가 margin의 wrong side에 위치할 수 있는 완화 조건을 비율적으로 정한 값이다. 그러므로, 완화변수들의 합 $\sum_i\xi_i$ 를 일정 상수 이하로 규제함으로써 어느 정도의 비율로 wrong-side positioning을 허가할 것인지 정할 수 있다. 이때 각 관측치가 잘못 분류되는 misclassification은 $\xi_i>1$ 인 경우 발생하므로, 만일 $\sum\xi_i\leq k$ 로 두면 이는 최대 $k$개의 관측치가 잘못 분류될 수 있음을 의미한다. 이렇게 완화변수를 이용해 margin의 misclassification을 허용하는 모델을 Soft Margin Classifier라고 하며, 구체적으로 모델이 계산되는 방식을 살펴보도록 하자.

Computing the Support Vector Classifier

여기서는 Soft Margin Classifier(이하 Support Vector Classifier, SVC)가 어떤 방식으로 계산될 수 있는지 살펴보도록 하자. 우선 앞선 최적화 문제를 다시 쓰면 다음과 같다.

\[\beta,\beta_0 = \arg\min{1\over 2}\Vert\beta\Vert^2+C\sum_{i=1}^N\xi_i\\ \text{subject to}\;\;\xi_i\geq 0,y_i(x_i^T\beta+\beta_0)\geq 1-\xi_i\tag{0}\]

여기서 상수 $C$는 앞서 언급한 완화변수들의 합을 규제하는 상수(constant)의 역할을 대체하는데, Hard margin classifier의 경우 $C=\infty$가 되어 각 slack variable들을 0으로 규제한다. 위 최적화문제를 Lagrangrian form으로 쓰면 Lagrange primal function은

\[L_p = {1\over2}\Vert\beta\Vert^2+ C\sum_i^N\xi_i-\sum_i^N\alpha_i[y_i(x_i^T\beta +\beta_0)-(1-\xi_i)]-\sum_{i=1}^N\mu_i\xi_i\tag{1}\]

과 같다. 최적화 문제를 풀기 위해 $\beta,\beta_0,\xi_i$ 에 대한 편미분계수를 0으로 하여 방정식을 구하면 다음과 같다.

\[\beta = \sum_{i=1}^N\alpha_iy_ix_i,\tag{2}\\ 0 = \sum_{i=1}^N\alpha_iy_i, \\ \alpha_i = C-\mu_i,\;\;\forall i\]

위 세 식들을 앞선 식 (1)에 대입하면 다음과 같은 dual objective function

\[L_D = \sum_{i=1}^N\alpha_i - {1\over2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jx_i^Tx_j\]

을 얻을 수 있다. 이때 최적화는 $0\leq\alpha_i\leq C$, $\sum_{i=1}^N\alpha_i y_i = 0$ 조건 하에서 $L_D$를 최대화하는 문제로 주어지게 된다. 또한 식 (2)의 세 식에 더불어 KKT(Karush-Kuhn-Tucker) 조건은 각 $i=1,\ldots,N$에 대해 다음 제약조건들로 주어지는데,

\[\alpha_i[y_i(x_i^T\beta+\beta_0)-(1-\xi_i)]=0,\\ \mu_i\xi_i = 0,\\ y_i(x_i^T\beta+\beta_0)-(1-\xi_i)\geq 0\tag{3}\]

제약조건 (2)와 (3)들을 모두 적용하면 dual problem에 대한 해는 다음과 같이 유일한 형태로 구해진다.

\[\hat\beta = \sum_{i=1}^N\hat\alpha_i y_ix_i\]

이때 KKT condition (3)의 첫번째, 세번째 식으로부터, 세번째 부등식의 좌변이 0이 아닌 경우 첫번째 식에 의해 각 계수 $\hat\alpha_i$는 0으로 주어진다. 반대로, 세번째 부등식을 등식으로 만족하는 관측값들에 대해서는 계수 $\hat\alpha_i$가 0이 아닌 값을 가지게 되고 이는 초평면 결정에 영향을 미치게 된다. 즉, 이러한 관측값들이 앞서 설명한 support vector가 된다.

Support Vector Machines and Kernels

앞서 설명한 support vector classifier는 Input feature space에서 선형 결정경계를 구현하는 모델이었다. 하지만 굳이 Input feature space에 얽매이지 않고, feature space에 basis expansion 또는 Kernel Method를 적용하여 결정경계를 좀 더 유연하게 확장할 수 있다. Support Vector Machine classifier(SVM)은 이처럼 feature space의 변형을 통해 차원을 확장, 혹은 축소하여 분류기를 만드는 방식을 의미하며, 일반적으로는 커널을 사용해 만든 support vector classifier/regressor을 의미한다고 보면 될 것이다.

Computation of SVM

앞서 SVC를 계산하는 과정에서, Lagrange dual function을 다음과 같은 형태로 정의했다.

\[L_D = \sum_{i=1}^N\alpha_i - {1\over2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jx_i^Tx_j\]

SVM에서는 위 식의 내적($x_i^Tx_j$) 대신에 feature transformation $h(x)$의(참고) inner product을 이용해 다음과 같이 정의한다.

\[L_D = \sum_{i=1}^N\alpha_i - {1\over2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j\langle h(x_i),h(x_j)\rangle\]

앞선 방식으로 위 최적화 문제를 해결하면, solution function $f(x)$는

\[f(x) = h(x)^T\beta+\beta_0\\ = \sum_{i=1}^N\alpha_i y_i\langle h(x),h(x_i)\rangle+\beta_0\]

으로 주어진다. 하지만 굳이 feature transformation의 내적을 구할 필요 없이, Kernel Trick을 이용하여 내적의 형태를

\[K(x,x')=\langle h(x),h(x')\rangle\]

으로 정의해버리면 된다. 이때 커널 함수 $K$로는 d차원 다항커널(polynomial kernel), 가우시안 방사커널(radial basis kernel) 등이 주어진다. 만일 두 Input $X_1,X_2$ 에 대해 2차원 다항커널($K(x,x’)=(1+\langle x,x’\rangle)^d$)을 적용하면

\[K(X,X') = (1+X_1X_1'+X_2X_2')^2\\ =1+2X_1X_1'+2X_2X_2'+(X_1X_1')^2+(X_2X_2')^2+2X_1X_1'X_2X_2'\]

가 되는데, 이를 basis expansion으로 나타내기 위해서는 $M=6$ 으로 설정하여(basis function의 개수) $h_1(X)=1,h_2(X)=\sqrt 2X_1,\ldots,h_6(X)=\sqrt2X_1X_2$ 로 다소 복잡한 설정이 필요하다. 이러한 방식으로 커널을 사용함으로써, SVM classifier의 solution function은 다음과 같이 주어진다.

\[\hat f(x) = \sum_{i=1}^N\hat\alpha_i y_iK(x,x_i)+\hat\beta_0\]

SVM Regression

SVM은 앞서 살펴보았듯이 근본적으로 초평면을 이용해 관측 데이터셋을 분류하는 모델이다. 그러나 분류 과정에서 SVM classifier의 몇몇 아이디어들을 어느 정도 차용한다면, SVM을 회귀 문제에도 적용시킬 수 있다. 우선 다음과 같은 선형회귀모형을 생각하고

\[f(x)=x^T\beta+\beta_0\]

이를 바탕으로 nonlinear한 일반화 과정을 다루어보도록 하자. 즉, $\beta$를 추정하는 과정에서 linear한 방법을 사용하는 것이 아닌 비선형함수 $V$를 이용해 다음과 같은 함수 $H$를 최소화하는 것이다.

\[H(\beta.\beta_0)=\sum_{i=1}^NV(y_i-f(x_i))+{\lambda\over2}\Vert\beta\Vert^2\]

이때 비선형함수 $V$는 회귀모형에서 실제값과 예측값을 측정하는 일종의 손실함수인데, 이중 하나로 다음과 같은 $\epsilon$-insensitive error measue

\[V_\epsilon(r)=(\vert r\vert -\epsilon)\cdot I[\vert r\vert \geq\epsilon]\]

을 사용할 수 있다. 이는 말 그대로 특정 값(epsilon) 이하의 오차를 무시하는 계산 방식인데, 앞서 살펴본 SVM classifier가 support vector를 제외한(결정경계로부터 멀리 떨어져있는) 관측값들을 무시하는 계산방식으로부터 유추된 것이다. 그런 의미에서 이를 support vector error measure라고도 부른다. 반면, Huber에 의해 제안된 error measure $V_H$는

\[V_H(r)=\begin{cases} r^2/2 & \text{if}\;\;\vert r\vert \leq c\\ c\vert r\vert -c^2/2 & \vert r\vert >c \end{cases}\]

로 주어지는데 이는 정해진 상수 $c$보다 큰 절대오차를 감소시켜 전체적으로 $f(x)$의 fitting 과정을 outlier들에 덜 민감하게끔 해준다. 이러한 방식들을 이용해 함수 $H$를 최소화하는 minimizer $\hat\beta,\hat\beta_0$을 구하면

\[\hat\beta = \sum_{i=1}^N(\hat\alpha_i^{\ast}-\hat\alpha_i)x_i\\ \hat f(x) = \sum_{i=1}^N(\hat\alpha_i^{\ast}-\hat\alpha_i)\langle x,x_i\rangle+\beta_0\]

으로 주어지는데, 여기서 각 $\hat\alpha,\hat\alpha^{\ast}$는 양수이며 다음과 같은 quadratic optimization problem

\[\min_{\alpha_i,\alpha^{\ast}_i}\epsilon\sum_{i=1}^N(\alpha_i^{\ast}+\alpha_i)-\sum_{i=1}^Ny_i(\alpha^{\ast}_i-\alpha_i)+{1\over2}\sum_{i,i'=1}^N(\alpha_i^{\ast}-\alpha_i)(\alpha_{i'}^{\ast}-\alpha_{i'})\langle x_i,x_{i'}\rangle\]

을 아래 제약조건들에서 푼 값들이다.

\[0\leq\alpha_i,\alpha_i^{\ast}\leq1/\lambda,\\ \sum_{i=1}^N(\alpha_i^{\ast}-\alpha_i) = 0,\\ \alpha_i\alpha_i^{\ast} = 0\]

그런데 위 세 제약조건에 의해 $(\hat\alpha_i^{\ast}-\hat\alpha_i)$의 값은 특정 부분집합을 제외하고 0이 되는데, 이때 0이 아닌 값을 갖는 $i$번째 관측값들을 support vector로 정의한다.

References

• Elements of Statistical Leraning