Tree 기반 알고리즘

Tree-Based Methods

Tree를 이용한 알고리즘은 기본적으로 Feature space^특성공간을 직사각형들의 집합으로 분할^partition하고, 각 집합들에 대해 매우 간단한 모델(e.g. constant)을 적용하는 원리이다. Tree를 기반으로 한 알고리즘에는 CART, ID3, C4.5 등이 있으며, 수많은 Tree를 적용시킨 Ensemble method으로 대표적인 RandomForest 같은 모델이 존재한다. 하지만 이런 다양한 Tree-based algorithm들을 관통하는 것은 특성공간을 여러 Region $R_m$들로 나누어 각각에 대해 다른 예측값(상수)을 부여하는 것이다. 즉,

\[\hat f(X) = \sum_{i=1}^kc_mI\lbrace \mathbf X\in R_m\rbrace\]

과 같은 형태로 prediction이 이루어진다. 결국 핵심은 Feature space의 Region을 얼마나 합리적으로 분할하는가이다. 이러한 분할은 Top-Down(가지치기) 형태로 표현가능한데, Input Space $\mathbf X$ 가 두 개의 Feature $X_1,X_2$로 표현될 때 아래 그림과 같이 5개의 Region을 top-down 방식으로 분할할 수 있다.

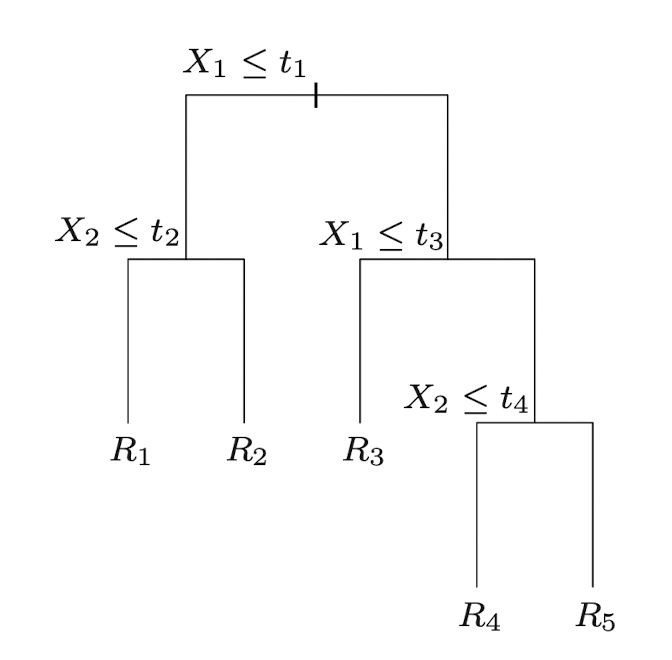
이때 각 분할이 일어나는 지점과 결과 Region들을 각각 node^노드라고 하며, 이렇게 표현된 Partition은 다음과 같이 도식화할 수 있다.

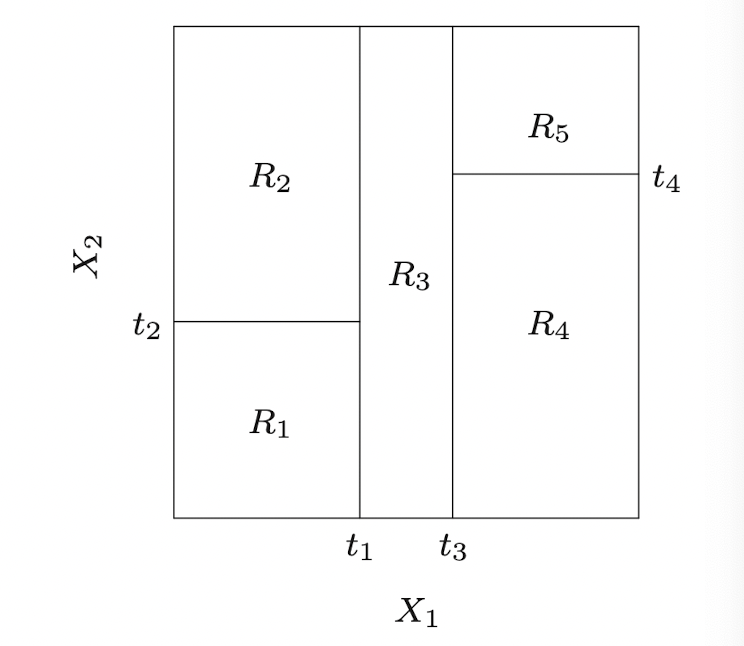
이러한 방식을 기반으로 Regression과 Classification의 두 가지 영역에서 모두 Tree-based algorithm을 이용할 수 있으며 이를 아울러 CART^{Classification and Regression Tree}라고 한다.

Regression Tree

$N$개의 observation에 대해 각각 $p$개의 feature, 즉 $x_i\in\mathbb R^p$ 인 회귀문제가 주어졌다고 하자. 앞서 설명한 Tree 방식으로 이러한 회귀문제를 해결하기 위해서는 알고리즘이 $p$개의 변수에 대해 어떤 값을 기준으로 분할하고, Tree가 전반적으로 어떤 형상을 취할 것인지 결정해야 한다. 우선, partition이 M개로 주어지고($R_1,\ldots,R_M$) 각각에 대해 constant 값이 주어지는 다음의 Tree 형태(엄밀히 말하면, Tree algorithm의 결과)를 생각하자.

\[f(x)=\sum_{m=1}^M c_mI(x\in R_m)\]

만일 손실함수를 Squared loss 로 정의하면, 각 Region에서 $\hat c_m = \text{ave}(y_i\vert x_i\in R_m)$ 이 되어야 할 것이다(각 Region별로 제곱합을 최소화해야 하므로). 이제 전체 데이터셋으로부터 region들을 분할하는 방법을 생각해보자. 예측변수의 어떤 variable $x_j$와 분할점(split point) $s$를 선택하게 되면 다음과 같은 두 Region

\[R_1(j,s)=\lbrace X\vert X_j\leq s\rbrace ,\;\;R_2(j,s)=\lbrace X\vert X_j>s\rbrace\]

을 얻는데, squared loss를 최소화하는 $j,s$를 찾고자 한다면 이는 다음의 최적화 문제가 된다.

\[(j,s) = \mathop{\arg\min}\limits_{j,s}\left[\min_{c_1}\sum_{x_i\in R_1(j,s)}(y_i-c_1)^2+\min_{c_2}\sum_{x_i\in R_2(j,s)}(y_i-c_2)^2\right]\]

또한, 최적값 $\hat j,\hat s$ 가 어떤 것으로 주어지든, squared loss에 대해 각 Region에서의 상수 $c$는 해당 Region에 속한 데이터들의 평균값으로 주어진다.

Cost-complexity pruning

그렇다면 얼마나 많은 변수들에 대해, 얼마나 많은 분할점을 지정해야 하는 것일까? 즉, Tree의 깊이^depth를 어느 정도로 설정해야 하는 것일까? 만일 Tree를 불필요할정도로 깊게 설정한다면, 주어진 훈련 데이터셋에 과적합되어 Validation 및 Test 과정에서 제대로 작동하지 않을 가능성이 높다. 이는 곧 Tree size가 일종의 hyperparmeter임을 의미하고, 학습과정에서 GridSearch 등을 통해 최적의 깊이를 찾아야 한다는 것이다.

이와 관련해 최적의 tree size를 찾는 알고리즘으로 pruning^가지치기 기법이 존재한다. 이는 Tree가 split되는 과정을 특정 깊이까지만 이루어지도록 설정하여 (minimum node size), 특정 깊이 이상의 가지를 제거하는 방식이다. 이때 가지치기가 이루어지는 구체적인 방식을 cost-complexity pruning이라고 하는데, 이에 대해서 살펴보도록 하자.

어떤 Tree model $T_0$에 대해 subtree ($T_0$보다 깊이가 얕은 tree) $T\subset T_0$ 을 정의하자. 즉, $T$는 $T_0$를 가지치기하여 생성되는 임의의 tree model을 의미한다. 이때 tree $T$에 대해 terminal nodes, 즉 가장 마지막 층에 위치한 노드에 index $m$을 부여하고 terminal node들에 해당하는 region을 $R_m$이라고 하자. 또한, terminal nodes의 개수를 $\vert T\vert $라고 두자.

\[\begin{aligned} N_m &= \text{number of elements in }\lbrace x_i\in R_m\rbrace \\ \hat c_m &= {1\over N_m}\sum_{x_i\in R_m} y_i\\ Q_m(T) &= {1\over N_m}\sum_{x_i\in R_m}(y_i-\hat c_m)^2 \end{aligned}\]

로 각각 Tree $T$의 terminal region의 원소 개수, Terminal region의 Least-squared constant, squared loss를 위와 같이 정의하자. 그러면 이로부터 다음과 같은 cost complexity criterion

\[C_\alpha(T)=\sum_{m=1}^{\vert T\vert }N_mQ_m(T) + \alpha\vert T\vert\]

이는 각 region에 대한 손실함수들의 합을 의미하는 첫 번째 항(COST)과 terminal node의 개수, 즉 tree model의 복잡성을 의미하는 두 번째 항을 포함하여 결과적으로 cost-complexity 사이의 tradeoff 관계를 표현한다. 이는 일반적인 머신러닝 모델의 Bias-Variance tradeoff와 일맥상통한다. 이렇게 cost complexity criterion을 정의하면, 이로부터 각 $\alpha$값에 대해 criterion을 최소화하는 subtree $T_\alpha$를 찾을 수 있다.

Classification Tree

Tree 모델이 분류문제에 사용되는 경우, 앞선 회귀문제에서와 같이 squared loss function 대신 분류에 최적화된 손실함수를 사용해야 한다. 이때 등장하는 개념이 바로 불순도^impurity인데, 이는 각 노드에 대해 예측된 반응변수와 실제 반응변수 사이의 오차를 측정하는 일종의 손실함수이다. 노드 $m$에 대해 region $R_m$이 대응되고, 이때 이 region에 $N_m$ 개의 데이터가 포함된다고 하자. 그러면

\[\hat p_{mk}={1\over N_m}\sum_{x_i\in R_m}I(y_i=k)\]

와 같이, 노드 $m$에서의 클래스 $k$ 비율을 정의할 수 있는데, $\hat p$인 이유는 모델을 바탕으로 계산한 표본비율이기 때문이다. 그렇다면, 노드 $m$에 대해서 각 클래스별 표본비율을 계산할 수 있고, 가장 단순한 예측 방법으로는 해당 노드의 클래스 예측값으로 $k(m)=\arg\max_k\hat p_{mk}$ 를 사용하면 될 것이다. 회귀문제의 경우와 마찬가지로 여기서도 model의 cost를 정의하는 함수 $Q_m(T)$를 정의할 수 있는데, 대표적으로 세 가지가 이용된다.

1. Misclassification error :

\[{1\over N_m}\sum_{i\in R_m}I(y_i\neq k(m)) = 1-\hat p_{mk}(m)\]

1. Gini Index^지니계수 :

\[\sum_{k\neq k'}\hat p_{mk}\hat p_{mk'} = \sum_{k=1}^K\hat p_{mk}(1-\hat p_{mk})\]

1. Cross-Entropy :

\[\sum_{k\neq k'}\hat p_{mk}\hat p_{mk'} = \sum_{k=1}^K\hat p_{mk}\log(1-\hat p_{mk})\]

예를 들어, 만일 이진 분류 문제에서 두번째 class에 대한 표본비율을 $p$라고 하면 앞선 세 유형의 cost function은 각각 $1-\max(p,1-p), \;\;2p(1-p),\;\;-p\log p-(1-p)\log(1-p)$ 가 된다. 세 종류의 함수는 모두 비슷하지만서도, Gini index와 Cross-entropy는 미분이 가능하다는 점에서 Classification 문제(Tree model 이외에도)의 손실함수로 자주 이용된다. 이렇게 정의한 cost function을 바탕으로, Regression Tree와 같이 Cost-complexity criterion을 최적화하는 Tree algorithm을 찾을 수 있다.

References

• Hastie, T., Tibshirani, R., Friedman, J. H., & Friedman, J. H. (2009). The elements of statistical learning: data mining, inference, and prediction (Vol. 2, pp. 1-758). New York: springer.