Boosting

Boosting Methods

Boosting^부스팅 은 21세기부터 statistical learning의 주요한 모델로 사용되고 있는 방법이다. 초기에는 분류 모델에 주로 이용되었으나, 회귀 문제로도 확장되어 사용된다. Boosting 방법들의 핵심 아이디어는 기본적인 Ensemble 기법, 즉 overfitting 가능성이 작은 weak classifier 여러개를 결합시킨 것을 바탕으로 예측을 진행하는 알고리즘이다. 그러나 Ensemble과의 차이점은, 이러한 weak classifier가 순차적으로^sequentially 구성된다는 것인데 이는 하나의 classifier의 결과를 이용해 다음 classifier의 결과를 개선시키는 방식으로 진행된다. 이러한 방식은 각 classifier가 독립적이지 않다는 것을 의미하며, 이는 각 classifier가 이전 classifier의 결과를 이용해 개선되는 방식으로 진행된다는 것을 의미한다. (이는 Bagging과는 다르다.)

Basic Idea of Boosting

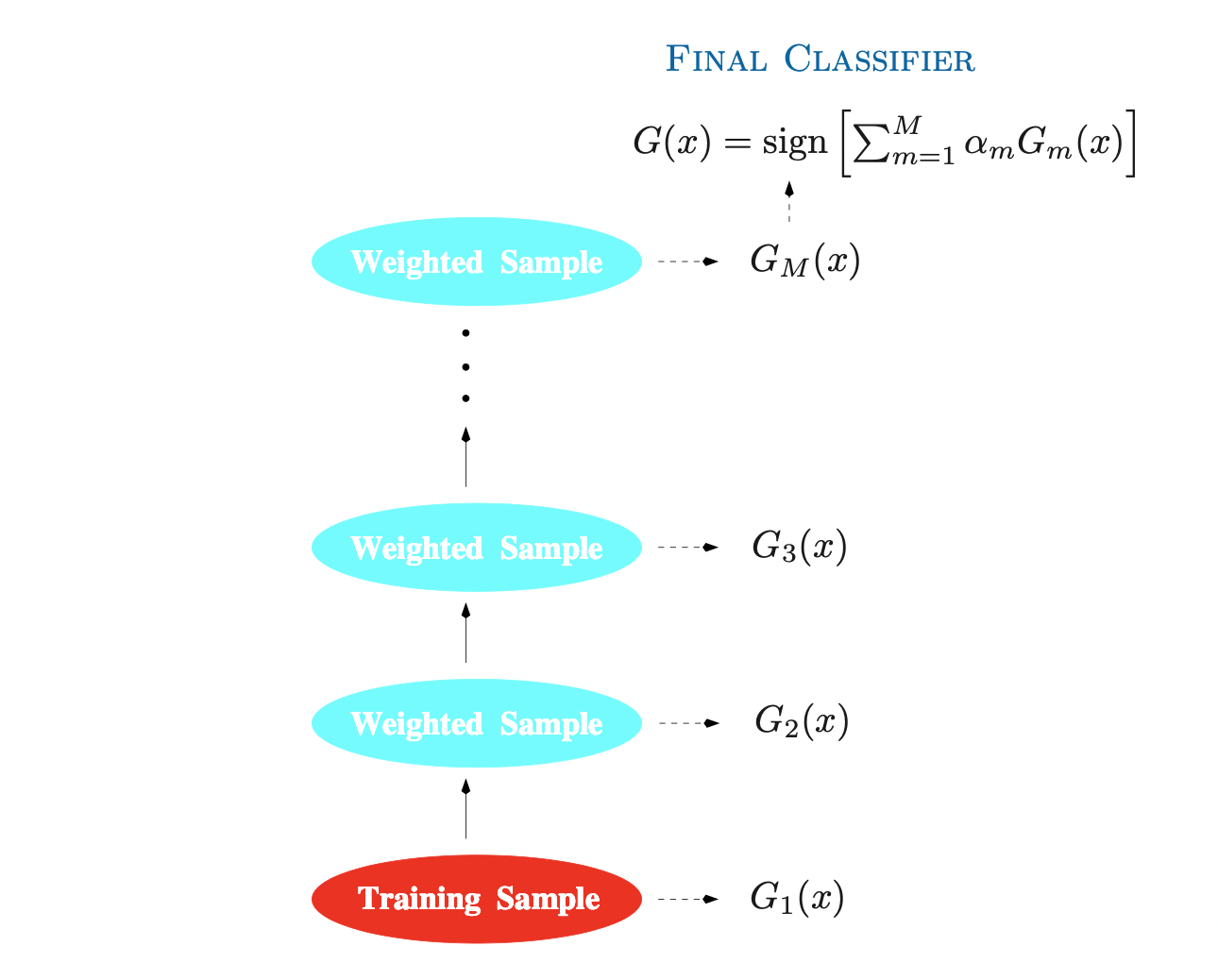Source : Elements of Statistical Learning

위 그림은 가장 대표적인 boosting 알고리즘인 AdaBoost.M1을 도식화한 것이다. 우선 AdaBoost 알고리즘을 바탕으로 boosting의 기본적인 학습과정을 살펴보도록 하자. 이진 분류 문제가 주어졌다고 가정하고, 반응변수가 \(Y\in\lbrace -1,1\rbrace\) 로 코딩되어있다고 하자. 예측변수는 벡터 $X$로 주어지며 이때 분류기 $G(X)$는 반응변수의 예측값 \(\hat Y\in\lbrace -1,1\rbrace\) 을 생성한다. 그러면 Training sample에 대한 오차를

\[\overline{\text{err}}={1\over N}\sum_{i=1}^N I(y_i\neq G(x_i))\]

로 정의할 수 있고, 예측값에 대한 기대오차(Expected error rate)는 $E_{XY}[I(Y\neq G(X))]$ 가 된다.

앞서 간단히 설명한 것 처럼, Boosting 알고리즘은 weak classifier들의 sequence $G_m(X)$ 를 생성하는 것인데, 여기서 weak 하다는 말은 오차율이 random guessing보다 미약하게나마 나은 것을 의미한다. 하지만 각 classifier 단계마다 데이터에 대한 가중치를 부여하여 이를 개선시켜나가고, 결과적으로 sequence의 모든 분류기를 합쳐 다음과 같은 최종 예측값을 도출한다.

\[G(x) = \text{sgn}\bigg(\sum_{m=1}^M \alpha_m G_m(x)\bigg)\]

여기서 각 분류기의 예측값들에 대한 가중치 $\alpha_1,\ldots,\alpha_M$ 의 경우 boosting algorithm을 통해 계산되며, 가중치를 곱하는 이유는 분류기의 열이 점차 개선되는 형태를 취하기 때문에, 좀 더 정확한 분류결과에 많은 가중치를 주기 위함이다.

반면, 분류기가 개선되는 과정과 동시에 훈련 데이터에 대한 변화도 발생한다. 이는 분류기와 비슷하게, 데이터셋의 각 관측값 $(x_i,y_i), i=1,\ldots,N$ 에 대해 가중치^{observation weight} $w_i$를 적용하는 방식이다. 다만, 첫 분류기에서는 데이터셋의 모든 관측값에 대해 동일한 $w_i=1/N$의 가중치가 적용되고 이후의 과정에서는 각 observation weight들이 개별적으로 수정된다. $m$번째 단계에서, 이전 단계의 분류기 $G_{m-1}(x)$ 에 의해 잘못 분류된 관측값들에 대해서는 observation weight를 증가시키고, 옳게 분류된 관측값들의 weight는 감소시킨다. 이러한 일련의 과정으로 정확한 분류가 어려운 관측값의 영향력이 커지며 분류기들은 그러한 데이터(이전에 잘못 분류된)들에 대해 좀 더 포커스를 맞추는 과정이 형성된다.

AdaBoost.M1.

앞서 설명한 Boosting 알고리즘인 AdaBoost의 구체적인 알고리즘은 다음과 같다.

1. observation weight들의 초기 설정 : $w_i = 1/N, i=1,\ldots,N$

2. $m=1,\ldots M$ 에 대해 다음 과정을 반복한다.

   1. 각 관측값들에 $w_i$를 적용한 데이터로 분류기 $G_m(x)$를 fitting한다.

   2. 앞선 분류기의 결과에 대한 error rate를 계산한다.

      \[\text{err}_m = \frac{\sum_{i=1}^N w_i I (y_i\neq G_m(x_i))}{\sum_{i=1}^N w_i}\]

   3. 분류기들의 가중치를 업데이트한다 :

      \[\alpha_m = \log\frac{1-\text{err}_m}{\text{err}_m}\]

   4. 관측값들의 가중치를 업데이트한다 :

      \[w_i\leftarrow w_i\cdot\exp[\alpha_m\cdot I(y_i\neq G_m(x_i))]\]

3. 최종 분류기

   \[G(x)=\text{sgn}\big(\sum_{m=1}^M\alpha_m G_m(x)\big)\]

   를 출력한다.

​ AdaBoost.M1 알고리즘은 Discrete AdaBoost로도 알려져있는데, 이는 base classifier, 즉 boosting의 기초를 이루는 개별 분류기들이 discrete class \(\lbrace -1, 1\rbrace\)을 출력하기 때문이다. 만일 base classifier가 확률값과 같이 실수값을 갖는다면, 이는 Real AdaBoost가 된다.

Boosting and Basis expansion

이전에 Spline Regression과 관련된 게시글에서 basis expansion에 대해 다루었던 적이 있었다. 이는 예측변수 matrix에 대해 새로운 변수를 추가하거나 기존 변수들을 대체하는 방식으로, 변환 $h_m$ 들에 대해 선형모형을(여기서 $\gamma_m$은 각 basis function의 모수를 의미한다 : ex. tree의 경우 split variable과 split point들을 의미함)

\[f(X) = \sum_{m=1}^M\beta_m h_m(X:\gamma_m)\]

로 표현하는 방식을 의미한다. 그런데, 이는 앞서 살펴본 Boosting의 표현식과 유사하다. 즉, 각 basis function $h_m$ 대신에 개별 분류기 $G_m(X)$ 를 대입하면 boosting 알고리즘과 basis expansion의 형태가 동일하다는 것을 확인할 수 있다. 일반적으로, basis expansion을 이용한 모델들은 training data 전체에 걸쳐 loss값의 평균을 구하고, 이를 최소화하는 방식으로 훈련이 이루어진다. 즉,

\[\min_{\lbrace \beta_m,\gamma_m\rbrace _1^M}\sum_{i=1}^N L\bigg(y_i, \sum_{m=1}^M\beta_m h_m(x_i:\gamma_m)\bigg)\tag{1}\]

의 형태로 최적화 과정이 이루어진다. 이때 대부분의 손실함수 $L(y,f(x))$와 각 basis function $h_m$ 들에 대해서 식 (1)의 최적화 과정은 꽤 복잡한 최적화 알고리즘을 요구한다.

Forward Stagewise Additive Modeling

Forward Stagewise additive modeling 방법은 위 식 (1)에 대한 최적화 문제의 근사치를 제공하는 방법 중 하나인데, 이는 연속적으로(sequentially) 기존 $\beta,\gamma$ 값들의 조정 없이 새로운 basis function을 추가하는 알고리즘이다. 자세한 알고리즘은 다음과 같다.

Forward Stagewise Additive Modeling

1. $f_0(x)=0$ 으로 초기화한다.

2. $m=1,\ldots ,M$ 에 대해 다음을 반복한다.

   1. \[(\beta_m,\gamma_m) = \mathop{\arg\min}\limits_{\beta,\gamma}\sum_{i=1}^N L(y_i, f_{m-1}(x_i)+\beta h_m(x_i:\gamma))\]
   2. $f_m(x)=f_{m-1}(x)+\beta_m h(x:\gamma_m)$ 으로 둔다.

예를 들어, squared loss가 사용되는 경우

\[L(y_i, f_{m-1}(x_i)+\beta h(x_i:\gamma)) = (e_{im}-\beta h(x_i:\gamma))^2\]

가 되는데 $e_{im}$은 $i$번째 관측값에 대한 현재 모델에서의 residual을 의미한다. 즉, squared loss에 대해서는 새로이 추가되는 항 $\beta_m h(x:\gamma_m)$ 은 현재 residual에 적합된 항이 된다.

AdaBoost and Forward Stagewise Additive Modeling

앞서 Forward Stagewise Additive Modeling 알고리즘에 대해 살펴보았는데, 다음과 같은 손실함수

\[L(y,f(x)) = \exp(-y f(x))\]

를 정의하면 forward stagewise additive modeling과 AdaBoost.M1 이 동일한 알고리즘을 보일 수 있다. AdaBoost 알고리즘에서는 각 basis function에 개별 분류기 $G_m(x) \in \lbrace -1,1\rbrace $ 이 대응되었다. 이를 Forward Stagewise Additive Modeling 알고리즘에 대입시키면, 새로이 추가되는 계수는

\[(\beta_m,G_m) = \mathop{\arg\min}\limits_{\beta,G}\sum_{i=1}^N\exp[-y_i(f_{m-1}(x_i)+\beta G(x_i))]\]

로 주어진다. $w_i^{(m)}=\exp(-y_i f_{m-1}(x_i))$ 로 두면 이는 각 parameter $\beta$나 분류기 $G$에 종속되지 않으므로, 위 식을

\[(\beta_m,G_m) = \mathop{\arg\min}\limits_{\beta,G}\sum_{i=1}^Nw_i^{(m)}\exp(-\beta y_iG(x_i))\tag{2}\]

로 다시 쓸 수 있다. 이때, 각 단계의 가중치 $w_i^{(m)}$이 이전단계의 모델 $f_{m-1}(x_i)$ 에만 의존하므로 이는 AdaBoost 알고리즘에서 전 단계의 분류기 결과를 통해 가중치를 업데이트 하는 과정과 대응할 수 있다. 이제 위 식 (2)에 대한 최적화 해를 다음과 같이 구해보도록 하자.

우선 식 (2)의 우변은 다음과 같이 표현되는데,

\[e^{-\beta}\cdot\sum_{y_i=G(x_i)}w_i^{(m)}+e^\beta\cdot\sum_{y_i\neq G(x_i)}w_i^{(m)} \\ = (e^\beta - e^{-\beta})\cdot\sum_{i=1}^N w_i^{(m)}I(y_i\neq G(x_i))+e^{-\beta}\cdot\sum_{i=1}^N w_i^{(m)}\]

여기서 $\beta>0$ 을 임의로 고정하면

\[G_m = \mathop{\arg\min}\limits_G\sum_{i=1}^N w_i^{(m)} I(y_i\neq G(x_i))\]

와 같은 형태로 $G_m$에 대한 최적화 문제를 얻을 수 있다. 또한, 이를 이용해

\[\text{err}_m = \frac{\sum_{i=1}^N w_i^{(m)}I(y_i\neq G_m(x_i))}{\sum_{i=1}^N w_i^{(m)}}\]

와 같이 minimized weighted error rate를 설정하면 $\beta$에 대한 최적해는

\[\beta_m = {1\over 2}\log\frac{1-\text{err}_m}{\text{err}_m}\]

으로 구해지는 것은 쉽게 보일 수 있다.

위와 같이 구한 최적해로 모델의 update 과정

\[f_m(x) = f_{m-1}(x) + \beta_m G_m(x)\]

를 가중치 $w_i$에 대한 update 과정으로 다음과 같이 다시 쓸 수 있다.

\[w_i^{(m+1)} = w_i^{(m)}\cdot e^{-\beta_m y_i G_m(x_i)}\]

여기서 $-y_iG_m(x_i) = 2I(y_i\neq G_m(x_i))-1$ 의 관계를 이용하면(쉽게 생각가능하다)

\[w_i^{(m+1)}=w_i^{(m)}\cdot e^{\alpha_mI(y_i\neq G_m(x_i))}\cdot e^{-\beta_m}\]

이 되고, $\alpha_m = 2\beta_m$ 은 AdaBoost에서의 분류기 가중치를 의미한다. 즉, 살펴본 것과 같이 AdaBoost.M1 알고리즘은 Exponential Loss criterion에 대해 Forward stagewise additive modeling을 이용한 최적화 알고리즘과 동일하다.

References

• Hastie, T., Tibshirani, R., Friedman, J. H., & Friedman, J. H. (2009). The elements of statistical learning: data mining, inference, and prediction (Vol. 2, pp. 1-758). New York: springer.