t-Stochastic Neighbor Embedding
t-distributed Stochastic Neighbor Embedding
Stochastic Neighbor Embedding
Stochastic Neighbor Embedding이란 고차원 공간에서 각 데이터들의 유사성(similarity)을 조건부 확률로 나타내는 차원축소 내지 클러스터링 기법을 의미한다. 가까운 데이터들에 대해서 조건부 확률을 크게 설정한다. 이를 수식으로 다음과 같이 정의하는데, 이 과정에서 정규분포를 이용한다.
\[p_{j\vert i} = \frac{\exp(-\Vert x_{i}-x_{j}\Vert^2/2\sigma_{i}^{2})}{\sum_{k\neq i}\exp(-\Vert x_{i}-x_{k}\Vert^{2}/2\sigma_{i}^{2})}\]이때 variance $\sigma_{i}^{2}$는 데이터 $x_{i}$ 를 중심으로 하는 정규분포의 분산을 의미한다. 반면, 앞선 고차원 데이터 $x_i,x_{j}$를 저차원으로 매핑한 데이터 $y_i,y_j$ 에 대해서도 다음과 같이 유사성 측도를 정의할 수 있다.
\[q_{j\vert i} = \frac{\exp(-\Vert y_{i}-y_{j}\Vert^2)}{\sum_{k\neq i}\exp(-\Vert y_{i}-y_{k}\Vert^{2})}\]만일 저차원 매핑 데이터 $y_i,y_j$가 고차원에서의 유사성을 완벽하게 재현한다면, 두 조건부 확률 $p_{j\vert i},q_{j\vert i}$ 의 값이 동일할 것이다. 즉, 이로부터 차원 축소가 잘 이루어진 $y_i,y_j$ 는 두 조건부확률분포의 차이를 최소화한다는 아이디어를 얻을 수 있고, 확률분포의 차이를 다음과 같이 Kullback-Leibler divergence로 나타내면 다음과 같은 비용함수(cost function)를 얻을 수 있다.
\[C=\sum_{i}KL(P_{i}\Vert Q_{i})=\sum_{i}\sum_{j}p_{j\vert i}\log\frac{p_{j\vert i}}{q_{j\vert i}}\]이 비용함수를 최소화하기 위해서 일반적으로 gradient descent 알고리즘을 사용하게 된다.
t-distributed Stochastic Neighbor Embedding
Symmetric SNE
KL divergence를 앞서 정의한 것처럼 조건부 확률분포들에 대해서 최소화할 수 있지만, 결합확률분포에 대해서도 최소화하는 방법을 생각할 수 있다. 이 경우 저차원 공간($y_i,y_j$에 대해)에서 비용함수는 다음과 같이 주어진다.
\[C=KL(P\Vert Q)=\sum_i\sum_{j} p_{ij}\log\frac{p_{ij}}{q_{ij}}\]이때 joint distribution에 대해서는 $p_{ij}=p_{ji}, q_{ij}=q_{ji}$ 가 성립하기 때문에, 이러한 SNE를 symmetric SNE 라고 정의한다. 또한, 저차원 공간에서의 유사성 측도 $q_{ij}$는 다음과 같이 주어지고
\[q_{ij} = \frac{\exp(-\Vert y_{i}-y_{j}\Vert^2)}{\sum_{k\neq l}\exp(-\Vert y_{k}-y_{l}\Vert^{2})}\]고차원 데이터 공간에서의 측도는
\[p_{ij} = \frac{\exp(-\Vert x_{i}-x_{j}\Vert^2/2\sigma^{2})}{\sum_{k\neq l}\exp(-\Vert x_{k}-x_{l}\Vert^{2}/2\sigma^{2})}\]으로 주어진다. 그런데, 이 경우 고차원 공간에서 어떤 데이터 $x_i$ 가 이상치인 경우 문제가 발생하게 된다. $i$번째 데이터가 이상치인 경우 $p_{ij}$가 모든 $j$에 대해 극단적으로 작아지는 문제가 발생하기 때문이다. 따라서 이를 극복하기 위해 symmetrized conditional probability를 다음과 같이 정의한다.
\[p_{ij}=\frac{p_{j\vert i}+p_{i\vert j}}{2n}\]Crowding Problem
일반적인 SNE, symmetric SNE는 Crowding problem이라고 하는 문제가 발생한다. 일반적으로 시각화 과정은 2차원 평면에 이루어지므로, 우선 주어진 고차원 데이터 $\mathbf{X}\subset\mathbb{R}^d$ 가 2차원 manifold $\mathcal{M}$ 위에 나타난다고 가정하자. 이러한 경우를 $\mathcal{M}$ 이 $\mathbb{R}^d$ 에 embedding 되어있다고 한다(manifold embedded in high dimensional space). 그런데, 만일 $\mathcal{M}$ 이 높은 차원의 intrinsic dimension을 가진다면 문제가 발생하게 된다. 여기서 intrinsic dimension이란, 데이터를 표현하기 위한 최소한의 변수의 수(차원)를 의미한다. 예를 들어 ten-intrinsic dimensional manifold라면, 11개의 서로 다른 data point $x_{i}, i=1,\ldots,11$ 이 있고 각각의 거리가 모두 같을 때(equidistant: $\Vert x_{i}-x_{j}\Vert$가 모두 동일할 때), 이들을 2차원 manifold에 매핑하는 것은 불가능하다. 직관적인 예제가 있어 이 글을 참고하면 좋을 것 같다.
t-SNE
t-SNE는 앞서 말한 Crowding Problem을 극복하기 위해 저차원 공간에서 유사성 측도를 heavy-tailed distribution으로 사용한다. Student t-distribution을 사용하며(cauchy distribution이기도 함), 다음과 같다.
\[q_{ij}=\frac{(1+\Vert y_{i}-y_{j}\Vert^{2})^{-1}}{\sum_{k\neq l}(1+\Vert y_{k}-y_{l}\Vert^2)^{-1}}\]Cost function의 그래디언트는 다음과 같이 계산된다.
\[\frac{\partial C}{\partial y_i}=4\sum_{j}(p_{ij}-q_{ij})(y_{i}-y_{j})(1+\Vert y_{i}-y_{j}\Vert^{2})^{-1}\]Perplexity
SNE에는 cost-function parameter(tuning parameter)로 사용하는 perplexity가 존재하는데, 다음과 같이 정의된다($H$는 Shannon entropy).
\[\begin{aligned} &\textrm{Perp}(P_{i}):=2^{H(P_{i})} \\ &H(P_{i})=-\sum_{j}p_{j\vert i}\log_{2}p_{j\vert i} \end{aligned}\]SNE 수행 과정에서 고차원 결합확률분포의 분산은 주어지는 것이 아니라 최적의 값으로 계산되는데, 이때 위와 같이 정의되는 perplexity가 smooth measure of the effective number of neighbors, 즉 적합한 $\sigma^{2}$ 값을 찾기 위한 탐색 과정에서의 parameter로서 작동한다.
Example. MNIST Data
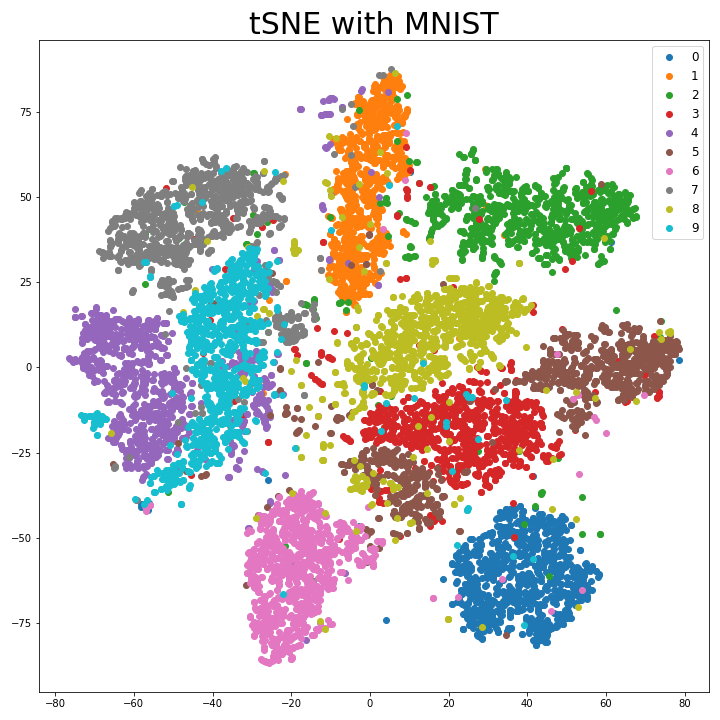
Sklearn 패키지에는 TSNE 모듈로 t-SNE를 간단하게 실행할 수 있게 되어있다. 이를 이용해 MNIST 데이터를 2차원 평면에 매핑한 결과 다음과 같다.
- 코드
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# MNIST dataset
from tensorflow.keras.datasets import mnist
# Load Data
from tensorflow.keras.datasets import mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# Select a subset of the data
target_indices = []
for i in range(10):
target_indices.extend(np.where(y_train == i)[0][:1000])
X_train = X_train[target_indices]
y_train = y_train[target_indices]
# Flatten X
X_train = X_train.reshape(X_train.shape[0], -1)
from sklearn.manifold import TSNE
# tSNE
tSNE = TSNE(n_components=2, perplexity=30, random_state=0)
tSNE.fit_transform(X_train)
# Plot with legend
df = pd.DataFrame()
df['x'] = tSNE.embedding_[:,0]
df['y'] = tSNE.embedding_[:,1]
df['label'] = y_train
plt.figure(figsize=(10,10))
for i in range(10):
plt.scatter(df[df['label']==i]['x'], df[df['label']==i]['y'], label=i)
plt.legend(fontsize = 12)
plt.title('tSNE with MNIST', fontsize=30)
plt.tight_layout()
plt.savefig('tSNE.png', facecolor='white')
References
- van der Maaten et al. - Visualizing Data using t-SNE (2008)
Leave a comment