따릉이 데이터 분석하기 (2) Linear Regression

따릉이 데이터 분석하기 (2) Linear Regression

먼저, 앞서 살펴본 따릉이 데이터셋을 이용해 가장 간단한 Linear Regression Model을 구현해보도록 하자. Python에는 statsmodels라는 패키지가 있는데, 이는 R에서 사용하는 형태로 통계분석을 가능하게 해주는 패키지이다(공식 문서 참고). 이를 이용해 선형모형을 만들고, 이를 개선시켜나가는 방법을 살펴보도록 하자. 먼저 필요한 패키지들은 다음과 같다.

import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt

OLS

Ordinary Least Square method를 이용한 가장 간단한 선형모형을 만들어보도록 하자. 우선, formula 작성의 편의를 위해 데이터를 로드하고 일부 값이 NaN으로 주어지므로, 이들을 제거하고 다음과 같이 column index들을 변경했다.

# Data Load
df_train = pd.read_csv('train.csv').dropna()
df_train.head(1)
df_train.columns = ['id', 'hour', 'temp', 'precip',
       'windspeed', 'humidity', 'visibility',
       'ozone', 'pm10', 'pm2_5', 'count']
print(df_train.head(1))
print(len(df_train))

	id	hour	temp	precip	windspeed	humidity	visibility	ozone	pm10	pm2_5	count
0	3	20	16.3	1.0	1.5	89.0	576.0	0.027	76.0	33.0	49.0

이를 바탕으로, 다음과 같이 OLS model을 만들고 fitting을 실행할 수 있다. 이때 formula는 R과 비슷한 형태로 ‘반응변수 ~ 예측변수 1 + 예측변수 2 …’ 의 형태를 취하는데, 여기서 예측변수가 categorical variable 인 경우에는 변수를 C(변수) 의 형태로 묶는다. 이 모델에서는 precipitation이 0 또는 1의 값을 갖는 범주형 변수이므로, dummy variable을 새로 만들지 않고 C(precip) 형태로 코딩하면 된다.

# OLS
model = smf.ols(
    "count ~ hour + temp + C(precip) + windspeed + humidity + visibility + ozone + pm10 + pm2_5",
    data = df_train
)
results = model.fit()
results.summary()

이를 실행하면 회귀분석의 요약결과(summary)를 아래와 같이 얻을 수 있다.

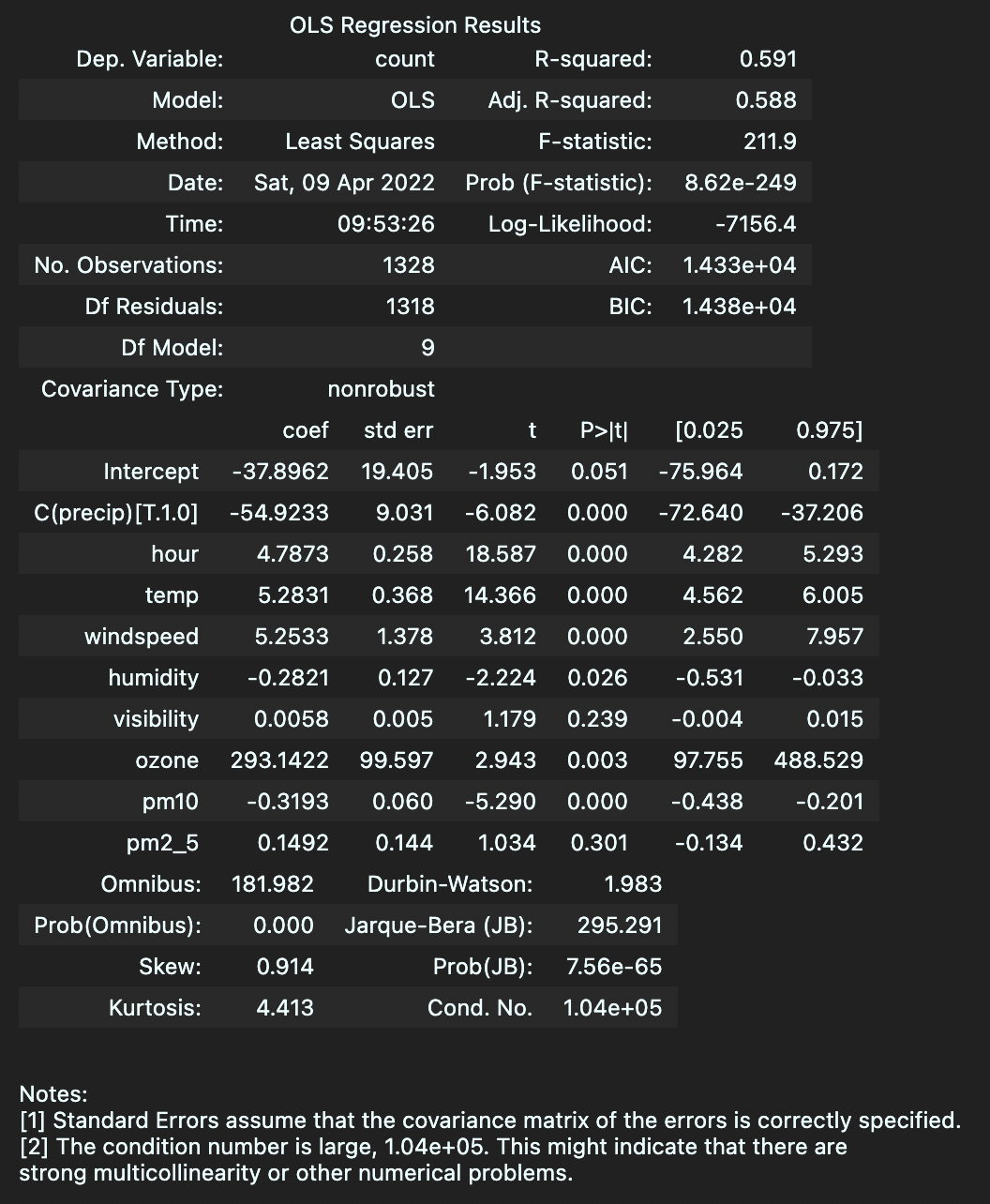
각 변수에 대한 coefficient $\beta$ 와 유의성(p-value, 여기서는 $P>\vert t\vert$) 뿐만 아니라 autocorrelation을 확인하는 Durbin-Watson statistic 등을 확인할 수있다. Notes [2]에서 강한 multicollinearity가 존재할 수 있을 가능성을 말해주고 있는데, 이는 예측변수 간의 상관관계가 존재할 수 있음을 의미한다.

VIF

앞서 설명한 것 처럼 예측변수 간의 상관관계가 발생하는 것을 Multicolinearity^{다중공선성}이라고 하는데, multicolinearity가 해당 변수를 제거해야 할 만큼 유의미한지 검증하는 방법으로 각 변수의 VIF^{Variance Inflation Factor}를 계산하는 방법이 있다. VIF란 Linear Regression을 이용한 방법으로, 자세한 내용을 설명하지는 않겠으나 아래 식

\[VIF_j = \frac{1}{1-R_j^2}\]

으로 정의된다. 즉, $j$번째 변수에 대한 VIF는 $R_j^2$을 바탕으로 계산되는데 이는 $j$번째 예측변수를 반응변수(Y)로, 나머지 $j-1$개의 예측변수들을 X로 하는 새로운 선형회귀모형을 구성할 때 이에 대한 R-squared value를 의미한다. 보통 10 이하의 VIF에 대해서는 acceptable하다고 판단한다.

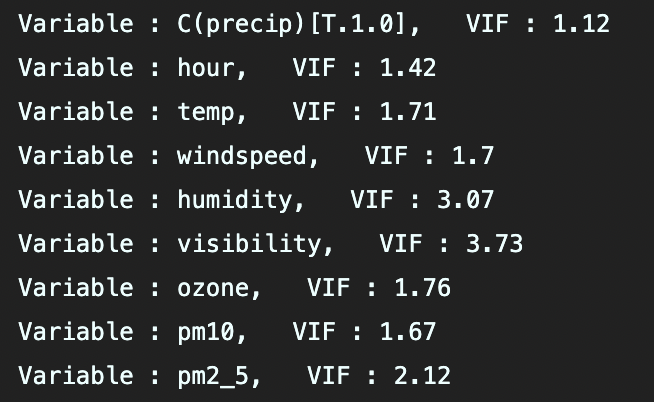
python에서는 statsmodels.stats에 variance_inflation_factor로 VIF를 계산할 수 있는 함수를 가지고 있다. 아래와 같이 코드를 실행하면 Intercept(상수항)을 제외한 나머지 변수들에 대해 각각 변수명과 VIF를 출력할 수 있다. 테스트 결과, visibility의 VIF가 3.73으로 가장 높긴 하지만, 매우 큰 값을 가지진 않으므로, 크게 문제되지는 않을 수준의 multicolinearity라고 판단되었다.

# VIF 
from statsmodels.stats.outliers_influence import variance_inflation_factor
for i in range(1, len(model.exog_names)):
    vif = variance_inflation_factor(model.exog, i)
    print(f'Variable : {model.exog_names[i]},   VIF : {vif.round(2)}')

Dummy variable

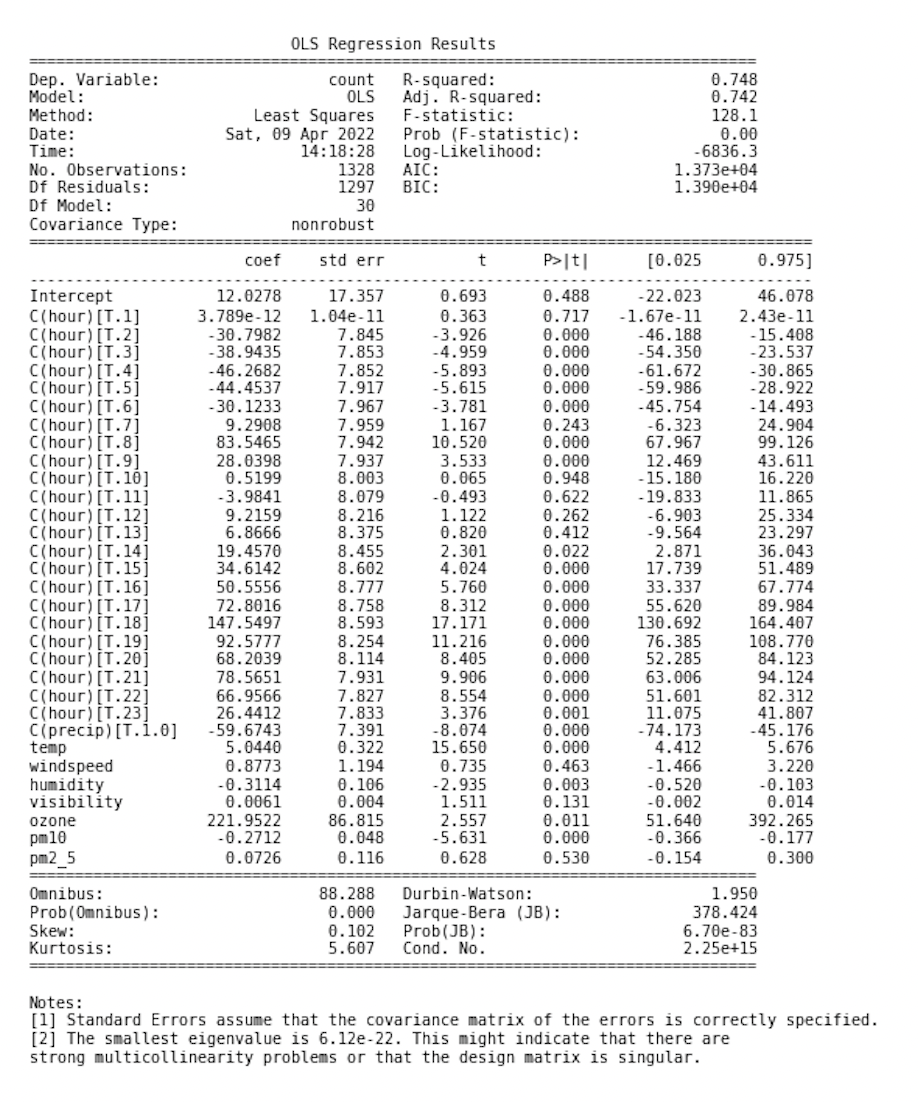
앞선 모델에서는 precip, 즉 강우상태만 dummy variable로 설정하였다. 사실 이전 글에서 살펴보았던 것 처럼 hour에 따른 이용량(Y)도 일정하지 않고, 시간대라는 것은 유의미하게 continuous한 변수가 아니므로 이를 dummy variable로 처리하는 방법 역시 고려해볼 수 있다. 아래 코드는 앞선 OLS model에서 hour을 categorical variable로 처리한 후, model의 summary 출력 내용을 별도의 이미지(아래와 같다)로 저장하는 코드이다.

# hour as dummy_variable
model = smf.ols(
    "count ~ C(hour) + temp + C(precip) + windspeed + humidity + visibility + ozone + pm10 + pm2_5",
    data = df_train
)
results = model.fit()
results.summary()

fig, ax = plt.subplots(1,1)
plt.rc('figure', figsize=(10, 15))
plt.text(0.01, 0.05, str(results.summary()), {'fontsize': 10}, fontproperties = 'monospace') # approach improved by OP -> monospace!
plt.axis('off')
plt.savefig('model_new.png', transparent = False, facecolor = 'white')

Model Assessment

앞선 OLS 모델은 전체 train dataset을 기반으로 회귀모형을 만든 것이므로, 모델의 성능을 직접적으로 평가하거나 과적합 정도를 파악하기 어렵다. 따라서 일반적으로 사용하는 방법인 train data, validation data를 임의로 구분하는 방법을 사용해 validation 과정을 추가하도록 하겠다. 또한, validation assessment 기준은 RMSE를 사용하도록 하겠다.

우선, 가장 많이 사용되는 머신러닝 라이브러리인 sklearn(scikit-learn)에 있는 train_test_split을 사용해 train data를 7:3의 비율로 나누었고, 929개의 train data, 나머지는 validation data로 사용했다.

# Model split
from sklearn.model_selection import train_test_split

X, y = df_train.iloc[:,1:-1], df_train.iloc[:,-1]
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.3, random_state=37)
print(len(X_train))

이후 모델링을 위해 dummy variable, constant variable을 처리하고 Modeling을 했고 마찬가지로 우선 summary()를 통해 선형모형의 fitting 결과를 확인하도록 하자. 여기서 drop_first=True로 설정한 이유는 dummy variable을 precip=0인 경우와 precip=1인 경우를 모두 생성해 불필요한 correlation의 형성을 막기 위함이다.

# Dummy, const treatment
X_train = pd.get_dummies(X_train, columns=['precip'], drop_first=True)
X_train = sm.add_constant(X_train)
X_val = pd.get_dummies(X_val, columns=['precip'], drop_first=True)
X_val = sm.add_constant(X_val)
# Modeling
ols = sm.OLS(y_train, X_train, missing='drop')
ols_res = ols.fit()
print(ols_res.summary())

이를 바탕으로, sklearn.metrics모듈에 있는 MSE 계산함수를 이용해 RMSE를 아래 코드와 같이 계산할 수 있다.

# Validation
from sklearn.metrics import mean_squared_error
pred_val = ols_res.predict(X_val)
rmse = mean_squared_error(y_val, pred_val)
print(f'RMSE : {np.sqrt(rmse).round(3)}') # Result : 53.242

Model Selection

이제부터는 OLS를 이용한 기본적인 선형모형을 변수 선택을 통해 개선시키는 방법을 연구해보도록 하자. 사실 선형모형이라는 한계 상, 모델 성능의 비약적인 개선을 기대하기는 어렵지만 데이터의 구조나 변수간의 관계를 면밀히 파악한다면 어느 정도의 개선을 이룰 수 있다.

회귀에 사용될 변수를 선택하는 방법은 매우 다양하다. 전진선택법, 후진선택법 등을 AIC/BIC 를 기준으로 실행하는 방법도 있고, Partial regression, CCPR plot 등을 이용해 특정 변수의 영향력을 파악하는 방법도 있다. 우선 Partial regression부터 살펴보도록 하자(Partial Regression에 대한 자세한 설명은 이 글을 참고하면 될 것이다).

Partial Regression Plot

fig = sm.graphics.plot_partregress_grid(ols_res)
plt.show()

위 코드를 통해 격자 형태로 각각의 변수와 반응변수 간의 Partial Regression Plot을 얻을 수 있는데, 아래 그림과 같다.

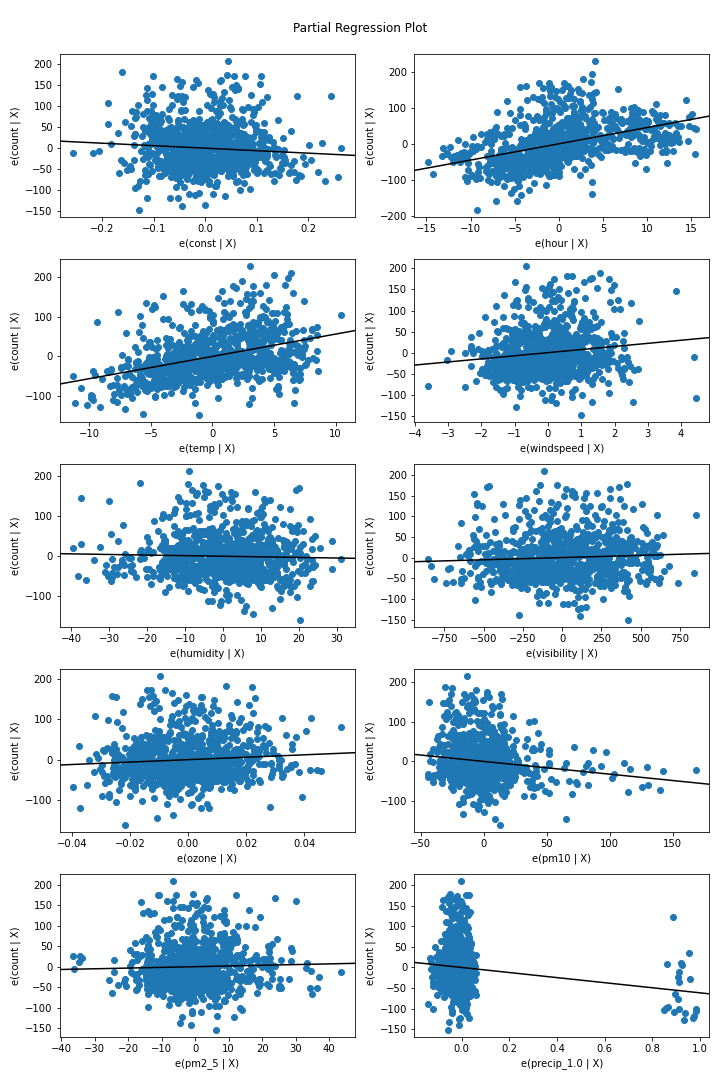
위 Partial Regression Plot을 살펴보면, humidity, visibility, pm2_5의 세 변수는 비교적 무의미한 영향을 갖는 예측변수로 파악할 수 있다.

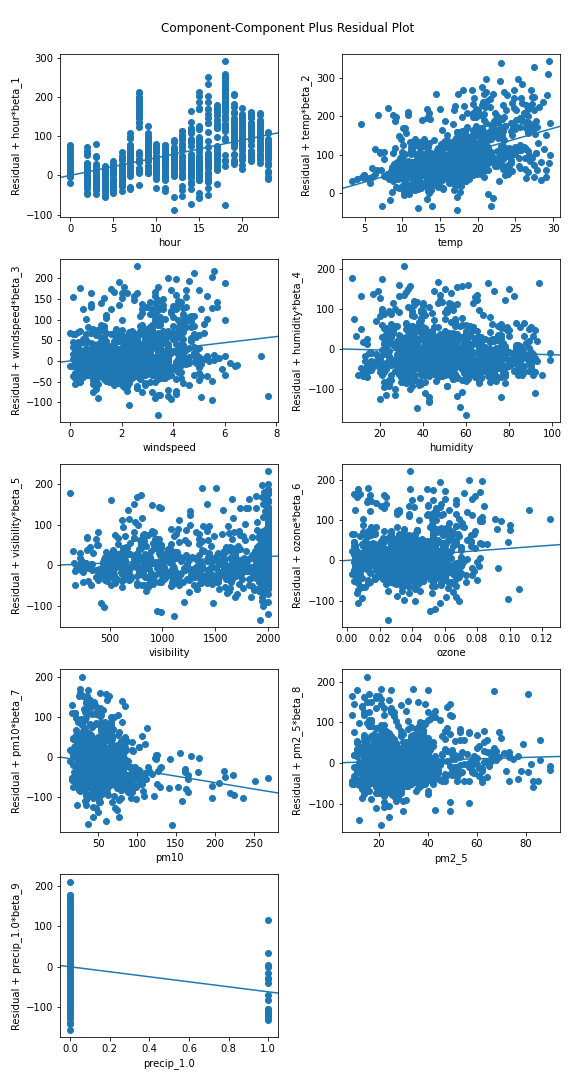
CCPR

CCPR(Component-Component plus Residual) plot도 partial regression plot과 마찬가지로 각 개별 변수의 영향력을 확인하기 위한 plot이다. 회귀모형

\[Y=X_1\hat\beta_1 +\cdots+X_p\hat\beta_p+\epsilon\]

이 주어질 때 개별 변수 $X_i$를 가로축으로, $X_i\hat\beta_i+\epsilon$ 을 세로축으로 그린 scatter plot이 바로 CCPR plot이다. 즉, 개별 변수의 추정 회귀계수를 표현하는 plot이라고 할 수 있다. 이 역시 statsmodels의 sm.graphics.plot_ccpr_grid로 다음과 같이 격자형 CCPR plot을 얻을 수 있다.

# CCPR
fig = plt.figure(figsize=(8,15))
sm.graphics.plot_ccpr_grid(ols_res, fig=fig)
plt.savefig('CCPR.png', transparent = False, facecolor = 'white')

Stepwise Selection

R에서는 step 함수를 이용해 전진/후진선택법을 쉽게 구현할 수 있으나, 안타깝게도 statsmodels 패키지는 이러한 모듈을 제공하고 있지 않다. 따라서 전진선택법과 후진선택법을 직접 구현하는 일이 필요하다. 코드는 아래와 같이 구현했고, 이때 변수 선택 기준은 AIC^{Akaike Information Criterion} 혹은 BIC, MSE를 사용할 수 있게끔 설정했는데(내용) 이들은 값이 낮을수록 더 좋은 성능임을 의미하므로 초기값을 무한(inf)으로 설정해 감소시켜나가는 공통적인 알고리즘을 갖기 때문이다.

# Forward/Backward-Stepwise Regression
def forward_ols(y, X, score):
    """
    endog y, Exog X
    score = 'aic', 'bic'
    """
    left_cols = list(X.columns.drop('const'))
    selected_cols = ['const']
    current_score, best_new_score = float('inf'), float('inf')
    aics = []
    while left_cols and current_score == best_new_score:
        scores = []
        for col in left_cols:
            sel_i = selected_cols + [col] # 기존 selected에 새로운 변수 하나씩만 추가
            ols_i = sm.OLS(y ,X[sel_i]).fit()
            scores.append(getattr(ols_i, score))
        best_i = np.argmin(scores) # AIC 최소로 하는 변수 index 가져오기
        best_new_score = scores[best_i]
        best_col = left_cols[best_i]
        # best AIC와 비교
        if current_score > best_new_score:
            left_cols.remove(best_col) # best_col remove
            selected_cols.append(best_col)
            current_score = best_new_score
            aics.append((best_col, current_score)) # AIC 저장
    model_best = sm.OLS(y, X[selected_cols]).fit()
    return model_best, aics

위 함수는 Forward-stepwise regression을 적용하여 변수들을 선택하고, 결과로는 최적 모델과 (각 단계에서 추가된 변수, 각 단계에서의 score 값) 의 순서쌍을 도출한다. 결과는 다음과 같다.

ols_f, aics_f = forward_ols(y_train, X_train, 'aic')
print(aics_f)
# Results
# [('temp', 10429.056), ('hour', 10149.413), ('visibility', 10102.013),('precip_1.0', 10077.424), ('windspeed', 10053.549), ('pm10', 10040.123), ('ozone', 10033.958)]

즉, 초기 상수항(const)만 있는 모델로부터 차례대로 temp, hour 등을 추가해나가며 점차 AIC 값을 감소시켜나갔음을 확인할 수 있다. 위 forward_ols 함수에서 score = 'bic'로 적용하면 BIC 값을 기준으로 Forward stepwise algorithm을 실행할 수 있는데, AIC와 동일한 결과가 도출됨을 확인할 수 있다. 이렇게 도출해낸 variable-selected model을 이용해 앞선 Full-model에 했던 것 처럼 validation data에 대해 RMSE를 구해보도록 하자.

# Validation of variable-selected model
def rmse_val(model, y_val, X_val):
    '''model : fitted model'''
    selected_vars = list(model.params.index)
    X = X_val[selected_vars]
    pred_val = model.predict(X)
    mse = mean_squared_error(y_val, pred_val)
    return np.sqrt(mse).round(3)

rmse_val(ols_aic_f,y_val,X_val) # Result : 53.5

RMSE는 53.242였던 Full Model에 비해 오히려 소폭 증가했음을 확인할 수 있다😅.

🖥 Full Code on Github: https://github.com/ddangchani/project_ddareungi