따릉이 데이터 분석하기 (6) Support Vector Machine

이번 글에서는 대표적인 머신러닝 모델인 SVM(Support Vector Machine)을 이용해 따릉이 이용 데이터의 분석을 진행해보도록 하자. 본래 SVM은 classification의 목적을 위해 고안된 기법으로, 데이터들의 레이블을 분류하는 기준이 되는 초평면을 찾아내는 과정이다. 그런데 이 과정의 아이디어를 이용해 SVM을 회귀 문제에서도 사용하게끔 할 수 있는데, 여기서 다룰 문제는 회귀문제 이므로 이를 이용해보고자 한다.(참고)

Scikit-learn에는 sklearn.svm 모듈로 서포트 벡터 머신 모델들을 제공한다. 회귀 문제의 경우 SVR(Support Vector Regressor)을 사용하면 되는데 이외에도 LinearSVR,NuSVR과 같은 다른 형태의 SVM regressor을 제공하고 있다. 우선 가장 기본적인 SVR 모듈을 이용해 회귀모델을 만들어보도록 하자.

SVR

이전에 살펴본 다른 모델들과 마찬가지로, sklearn의 Pipeline을 이용해 모델을 순차적으로 구성할 것인데, 데이터 불러오기 및 전처리 과정은 이전에 사용한 코드와 유사하나 SVM의 경우 Input data의 스케일(scale)에 영향을 받기 때문에 여기서는 hour 변수까지 StandardScaler()로 처리했다(편차를 표준편차로 나눠주는 과정이 포함되었다는 의미임). 이를 바탕으로, 우선 디테일한 hyperparameter의 조정 없이, SVM에서 사용할 커널을 결정하기 위해 세 가지 커널을 바탕으로 score들을 비교해보도록 하자. 여기서는 RBF, Linear, Polynomial kernel(degree = 3)의 세 가지를 이용했다. gamma, epsilon, C 등의 여타 hyperparmeter는 커널을 결정한 이후에 Gridsearch로 조절해보도록 하자. 코드는 다음과 같다.

# 3 kernel SVR models
svr_rbf = Pipeline(
    steps=[("preprocessor",preprocessor),
    ("svr",SVR(kernel="rbf", C=100, gamma=0.1, epsilon=0.1))]
)
svr_lin = Pipeline(
    steps=[("preprocessor",preprocessor),
    ("svr",SVR(kernel="linear", C=100, gamma=0.1, epsilon=0.1))]
)
svr_poly = Pipeline(
    steps=[("preprocessor",preprocessor),
    ("svr",SVR(kernel="poly",degree=3 , C=100, gamma=0.1, epsilon=0.1))]
)
models = [svr_rbf,svr_lin,svr_poly]
for svr in models:
    svr.fit(X_train, y_train)

# Metric for each model

for svr in models:
    y_pred = svr.predict(X_val)
    rmse = np.sqrt(mean_squared_error(y_val,y_pred))
    print('Kernel: %s  Score: %.3f' % (svr.named_steps['svr'].kernel, rmse))
    
# Kernel: rbf  Score: 44.902
# Kernel: linear  Score: 52.397
# Kernel: poly  Score: 48.031

각 커널에 대해 svr_rbf, svr_lin, svr_poly로 대응하는 모델을 만들었고, train data를 이용해 모델을 fitting 한 후, validation data에 대한 RMSE score를 각각 출력하도록 하였다. 그 결과(밑부분 주석) Gaussian RBF kernel에서 가장 낮은 RMSE를 얻을 수 있었는데, 어떤 형태로 회귀모델이 형성되었는지 시각적으로 살펴보기 위해 이번에는 이전에 다루어본 것 처럼 PCA를 이용해 첫 번째 주성분에서의 정사영을 통해 회귀가 이루어지는 양상을 살펴보도록 하자.

SVR with PCA

# SVR with PCA and Plot
from sklearn.decomposition import PCA
svr_rbf = Pipeline(
    steps=[("preprocessor",preprocessor),
    ('pca',PCA(n_components=3)),
    ("svr",SVR(kernel="rbf", C=100, gamma=0.1, epsilon=0.1))]
)
svr_lin = Pipeline(
    steps=[("preprocessor",preprocessor),
    ('pca',PCA(n_components=3)),
    ("svr",SVR(kernel="linear", C=100, gamma=0.1, epsilon=0.1))]
)
svr_poly = Pipeline(
    steps=[("preprocessor",preprocessor),
    ('pca',PCA(n_components=3)),
    ("svr",SVR(kernel="poly",degree=3 , C=100, gamma=0.1, epsilon=0.1))]
)
models = [svr_rbf, svr_lin, svr_poly]
kernel_labels = ['Gaussian RBF','Linear','Polynomial']

fig, axes = plt.subplots(nrows=3, ncols=1, figsize = (10,15))
cmap = ['darkgreen', 'navy', 'magenta']
for idx, svr in enumerate(models):
    svr.fit(X_train, y_train)
    pca = svr[0:2] # Pipeline until PCA
    xs, ys = zip(*sorted(zip(pca.transform(X_val)[:,0],svr.predict(X_val)))) # projected X and predicted y
    axes[idx].scatter(pca.transform(X_val)[:,0], y_val, alpha = 0.4, label='training data')
    axes[idx].plot(xs, ys, label = 'predicted data with kernel = ' + kernel_labels[idx], color=cmap[idx], linewidth = 2)
    axes[idx].legend(fontsize = 12, loc='upper right')
    axes[idx].set(xlabel = 'First Principal Component', ylabel='Y')

fig.suptitle("Support Vector Regression with Kernels", fontsize = 14)
plt.savefig("plots/SVR_with_PCA_by_kernel.png", facecolor = 'white', transparent = False)

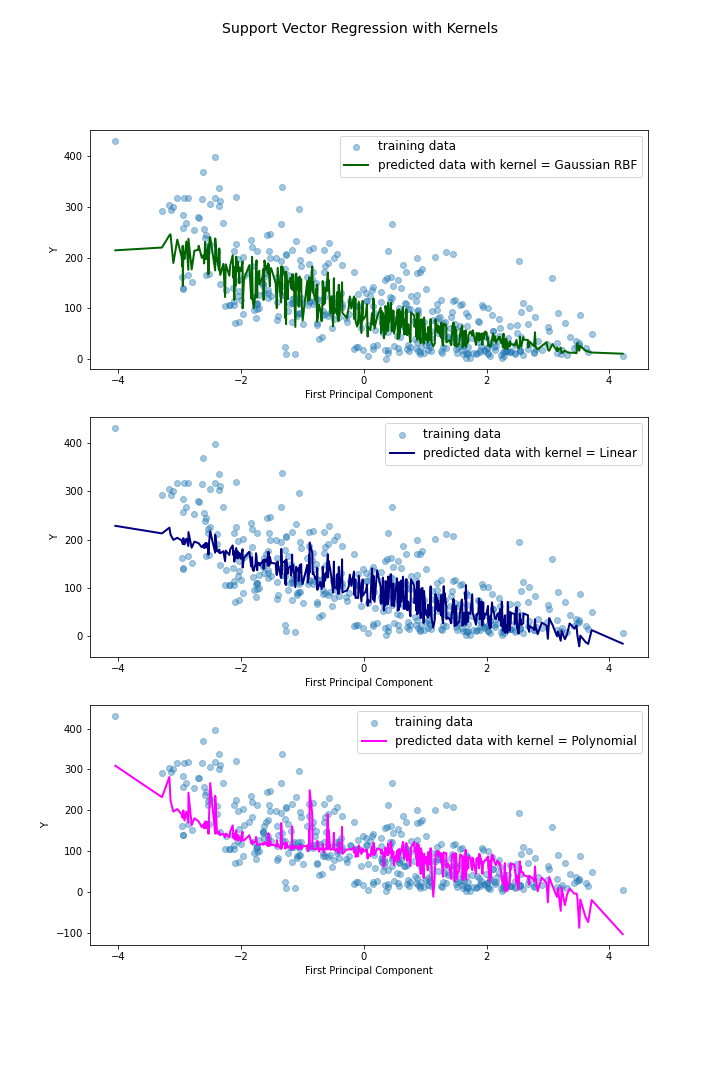
SVR_with_PCA_by_kernel

위 코드를 실행하면 바로 위의 plot을 얻을 수 있는데, 분류 문제가 아닌 회귀 문제이므로 각 커널이 어떻게 작동했는지 명확히 파악하는 것이 다소 어렵고, 과적합 유무도 시각적으로는 명확히 구분되지 않는다. 따라서 여기서는 그냥 Validation RMSE가 가장 낮게 도출된 RBF kernel을 그대로 사용하여, 이제 세부 하이퍼파라미터를 조율해보도록 하겠다.

Hyperparameter Tuning

이번에는 RBF kernel을 바탕으로 다른 hyperparmeter들을 gridsearch로 조율해보도록 하자. 우선 hyperparmeter C는 다음의 Lagrangrian form에서의 비용 상수 $C$에 반비례한다(이는 classification SVM의 form이다(참고)).

\[\beta,\beta_0 = \arg\min{1\over 2}\Vert\beta\Vert^2+C\sum_{i=1}^N\xi_i\\ \text{subject to}\;\;\xi_i\geq 0,y_i(x_i^T\beta+\beta_0)\geq 1-\xi_i\tag{0}\]

$C>0$의 값은 기본값 1로 설정되어있는데, $C$ 값이 커지면($C\uparrow+\infty$) 각 slack variable $\xi_i$ 들이 0에 수렴하여 결과적으로 Hard margin classifier가 되고, 반대의 경우는 규제가 완화된다. SVR()에서의 Hyperparmeter C는 이와 반대로 값이 작아질수록 강한 규제가 작동하는 방식이다,

다른 hyperparmeter인 epsilon은 설정된 값 이하의 오차를 무시하는 support vector regression에서의 알고리즘을 의미하는데, 자세한 내용은 위 링크의 SVR 내용을 참고하면 된다. 마지막으로 hyperparmeter gamma는 커널함수(rbf, sigmoid, polynomial의 경우만 존재한다.)

\[K(x,x') = \exp(-\gamma\Vert x-x'\Vert^2)\]

에 포함된 $\gamma$ 값을 의미한다. gamma = 'auto' 로 설정된 경우 일반적으로 사용되는 값인 $1/p$ ($p$ 는 input data의 특성 수를 의미한다) 를 사용한다.

해당 hyperparmeter들에 대한 grid를 exponential 형태로 설정했으며, 이를 바탕으로 다음과 같은 코드를 통해 GridSearch를 진행하였다.

# Hyperparameter Tuning with GridSearch
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import make_scorer
# RMSE def for Gridsearch Scoring
def rmse(y_true, y_pred):
    mse = mean_squared_error(y_true, y_pred)
    return(np.sqrt(mse))
rmse_score = make_scorer(rmse, greater_is_better=False)

# Model and grid setting
svr = Pipeline(
    steps=[("preprocessor",preprocessor),("svr",SVR())]
)
param_grid = {
    'svr__C' : np.logspace(-2,2,5), # Regularization
    'svr__kernel' : ['rbf'],
    'svr__epsilon' : np.logspace(-3,0,4), # epsilon at SVM regressor
    'svr__gamma' : ['auto', 0.1, 0.01]
}
svr_grid = GridSearchCV(svr, param_grid, verbose=2, scoring=rmse_score)
svr_grid.fit(X_train, y_train)

최적의 hyperparmeter 조합을 다음과 같이 찾아내고 이를 바탕으로 Validation data에 대한 RMSE error를 구한 결과 다음과 같다.

# Gridsearch result
from copy import deepcopy
best_params = deepcopy(svr_grid.best_params_)
for key in param_grid.keys():
    best_params[key[5:]] = best_params.pop(key)
print(best_params) 
# {'C': 100.0, 'kernel': 'rbf', 'epsilon': 1.0, 'gamma': 0.1}

# Best SVR model
svr_best = Pipeline(steps=[('preprocessor',preprocessor),('svr',SVR(**best_params))])
svr_best.fit(X_train, y_train)
# Validation RMSE
y_pred = svr_best.predict(X_val)
rmse(y_val, y_pred).round(3) # 44.871

처음에 임의로 설정했던 hyperparmeter 조합에 비해 validation error가 거의 개선되지 못했으며, 특히 규제 hyperparmeter $C$의 경우 가장 큰 값을 취하려하는 것으로 보아 SVM 알고리즘에서의 규제 자체가 유의미하게 작동하지 못함을 확인할 수 있다. 또한, 여기서 사용된 SVR 방법은 기본적인 $\epsilon$-SVR로, 하이퍼파라미터인 $\epsilon$은 모델이 오차를 얼마나 유연하게 받아들일 지(tolerate)에 대한 값이다(참고). 그러나, 위 Gridsearch 과정에서 epsilon 값은 grid중 가장 큰 값(여기서는 $1.0$)을 택하려는 경향을 보였다. 즉, 앞서 얻은 SVR 모델은 $1.0$ 이하의 오차에 대해 insensitive한 모델이다. 그런데, 우리는 앞서 위 모델의 전처리 과정에서 response variable $Y$(이용 횟수 : count)에 대해 표준화 스케일을 적용한 바 있다.

따라서, 스케일된 반응변수에 대해 1.0 이하의 오차를 무시한다는 것은 데이터셋의 1표준편차만큼의 오차를 무시한다는 것이다. 정규분포 가정하에 관측값으로부터 1표준편차의 범위는 68%의 관측값 비율을 의미하므로, 이는 사실상 SVR 메커니즘이 무의미할 정도로 형편없이 동작한다는 의미이다.

NuSVR

이번에는 SVR의 변형 형태중 하나인 NuSVR(참고) 모델을 이용하여 분석을 진행해보도록 하겠다. NuSVR에서는 다른 하이퍼파라미터인 Nu($\nu$) 값을 지정해주어야 하는데, $\nu$ 값으로 epsilon값을 컨트롤하기 때문에 여기서는 하이퍼파라미터 epsilon을 별도로 지정해줄 필요 없다. 이번에도 앞선 경우와 마찬가지로 Gridsearch를 이용해 hyperparmeter tuning을 진행해보도록 하겠다.

# NuSVR
from sklearn.svm import NuSVR
nusvr = Pipeline(
    steps=[("preprocessor",preprocessor),("svr",NuSVR())]
)
param_grid = {
    'svr__nu' : [0.01, 0.1, 0.5, 0.75],
    'svr__C' : np.logspace(-2,2,5), # Regularization
    'svr__kernel' : ['rbf','linear'],
    'svr__gamma' : ['auto', 0.1, 0.01]
}
nusvr_grid = GridSearchCV(nusvr, param_grid, verbose=2, scoring=rmse_score)
# Fit
nusvr_grid.fit(X_train, y_train)

앞서 SVR의 best_params를 구하는 코드를 이용해 다음과 같이 best parameter를 얻을 수 있다.

{'nu': 0.5, 'C': 100.0, 'kernel': 'rbf', 'gamma': 0.1}

nu는 default 값인 0.5를 채택했고, kernel 종류와 gamma 값도 SVR 결과와 동일했다. 다만, 여기서도 C 값이 제일 큰 값을 택하였기에 모델의 규제항 자체가 유의미하게 작동하지 못한다는 사실을 확인할 수 있다. 마찬가지로, 이렇게 얻은 best parameter들을 이용해 다음과 같이 validation score을 계산했다. 작은 감소는 있었지만, 크게 유의미하다고 보여지지 않는다. 종합적으로 고려해볼 때 Support Vector Regression이 본 Problem에 적합하지 않는다고 판단되는데, 아마 categorical variable이나, 특히 시간대와 같은 변수로 인해 그러한 현상이 발생하는 것으로 추측된다.

# Best NuSVR model
nusvr_best = Pipeline(steps=[('preprocessor',preprocessor),('svr',NuSVR(**best_params))])
nusvr_best.fit(X_train, y_train)
# Validation RMSE
y_pred = nusvr_best.predict(X_val)
rmse(y_val, y_pred).round(3) # 43.844

References

  • Scikit-Learn 공식 문서 : https://scikit-learn.org/stable/auto_examples/svm/plot_svm_regression.html#sphx-glr-auto-examples-svm-plot-svm-regression-py

  • 🖥 Full code on Github : https://github.com/ddangchani/project_ddareungi

Leave a comment