따릉이 데이터 분석하기 (3) Modified Linear Methods

이번 글에서는 Linear regression을 계속 다룰 것인데, 그중에서도 regularization method나 spline regression과 같은 변형된 방법들을 다루어보고자 한다(역시 Regression 문제가 Linear Model로 다루기 최적인듯 하다🤣). 우선 Lasso, Ridge 등을 포함하는 Shrinkage method 들을 구현해보도록 하자. 이러한 Linear Method들은 모두 이전에 사용했던 statsmodels 패키지를 이용해 구현할 수 있다.

Shrinkage Methods

Data load와 train_test split의 과정은 이전 게시글들을 살펴보는 것으로 갈음하고, 바로 모델을 구현해보도록 하자. 여기서는 회귀계수의 Regularization을 통해 모델을 설정하는 방법들을 다룰 것인데, 자세한 내용은 Linear Regression 게시글을 살펴보면 될 것이다.

Ridge/Lasso/ElasticNet

statsmodels패키지로 전 게시글에서 OLS 모델을 만든 뒤, .fit() 메서드를 사용해 모델을 fitting하고 이를 이용해 summary()로 모델의 성능을 파악하거나, 모델의 성능 지표를 attribute로 불러오는 등의 작업을 했었다. 이때, 일반적인 fit 메서드 대신 fit_regularized() 메서드를 사용하면 Elastic-Net 형태의 regularization term이 추가된 fitting을 진행할 수 있다. 이때 parameter로 alpha=, L1_wt= 이 요구된다. 우선 아래 코드를 보도록 하자.

# fit_regularized 
ols_lasso = sm.OLS(y_train, X_train).fit_regularized(method="elastic_net", alpha = 0.1, L1_wt=1)
ols_ridge = sm.OLS(y_train, X_train).fit_regularized(method="elastic_net", alpha = 0.1, L1_wt=0)
ols_elnet = sm.OLS(y_train, X_train).fit_regularized(method="elastic_net", alpha = 0.1, L1_wt=0.5)

위 코드에서 alpha=0.1은 regularization term에 곱해진 상수, 즉 규제 강도를 의미하며($\alpha\cdot\Vert\beta\Vert$), L1_wt=1.0은 Elastic-Net에서 L1 Regularization Term을 1만큼 사용하고 L2 Norm 을 0만큼 사용해 Lasso method를 사용함을 의미한다. 반대로, L1_wt=0은 Ridge method를 사용함을 의미한다. 마지막 코드는 Elastic-Net으로 L1 norm과 L2 norm에 모두 0.5씩의 가중치를 부여하여 규제하는 것을 의미한다.

각각의 모델은 추정된 parameter 값을 불러올 수 있는 .params 메서드를 가지며, 다음과 같이 확인할 수 있다.

print(ols_lasso.params)
## result
const         133.952147
hour            4.794684
temp            4.729933
windspeed       5.716406
humidity       -1.245661
visibility     -0.035364
ozone           0.000000
pm10           -0.634140
pm2_5          -0.639569
precip_1.0    -58.274955
dtype: float64

이때 모델에서 alpha값은 hyperparameter이므로, alpha 값을 조정하며 각 예측변수들의 coefficient에 어떠한 영향을 미치는지 파악해보도록 하자. 다음 코드는 alpha 값을 $10^{-3}$부터 $10^1$까지 총 5개 값을 취할 수 있게끔 하여 각 alpha값에 대한 ridge regression의 각 회귀계수를 데이터프레임으로 반환한다.

# changing alpha - ridge
alpha = np.logspace(-3,1,5) # range of alpha(exponential)
data = []
for i, a in enumerate(alpha): 
    ridge = sm.OLS(y_train, X_train).fit_regularized(method = 'elastic_net', L1_wt = 0, alpha = a)
    data.append(ridge.params)
df_ridge = pd.DataFrame(data, index = alpha).T.round(3)
df_ridge.index = X_train.columns
print(df_ridge)

결과는 다음과 같다.

	0.001	0.010	0.100	1.000	10.000
const	-47.021	-19.137	-2.610	-0.172	0.031
hour	4.570	4.542	4.497	4.631	4.393
temp	5.831	5.658	5.558	5.548	4.641
windspeed	8.344	8.056	7.287	4.580	1.369
humidity	-0.242	-0.424	-0.561	-0.597	-0.591
visibility	0.008	0.002	0.000	0.002	0.013
ozone	52.863	6.231	0.684	0.095	0.020
pm10	-0.331	-0.368	-0.381	-0.356	-0.281
pm2_5	0.165	0.067	0.011	0.009	0.174
precip_1.0	-59.797	-42.783	-11.126	-1.313	-0.127

alpha 값이 커질수록 각 회귀계수가 0에 수렴함을 확인할 수 있으며, 이번에는 plot을 통해 ridge, lasso, elastic-net($\alpha=0.5$) 일 때의 변화를 비교해보도록 하자.

# Plot : coef vs. alpha
fig = plt.figure(figsize = (10,20))
ax1 = plt.subplot(3,1,1)
plt.semilogx(df_ridge.T) # ridge
plt.xticks(np.logspace(-3,1,5), labels=np.log10(alpha))
plt.title('Ridge')

ax2 = plt.subplot(3,1,2)
plt.semilogx(df_lasso.T) # lasso
plt.xticks(np.logspace(-3,1,5), labels=np.log10(alpha))
plt.title('Lasso')

ax3 = plt.subplot(3,1,3)
plt.semilogx(df_elnet.T) # elnet
plt.xticks(np.logspace(-3,1,5), labels=np.log10(alpha))
plt.title('Elnet')

위 코드를 실행하면, 다음과 같은 세 그래프를 얻을 수 있는데, Lasso method가 계수의 수렴이 가장 느리며, Ridge가 가장 빠르게 수렴함을 확인할 수 있다.

스크린샷 2022-04-11 오후 4.07.18

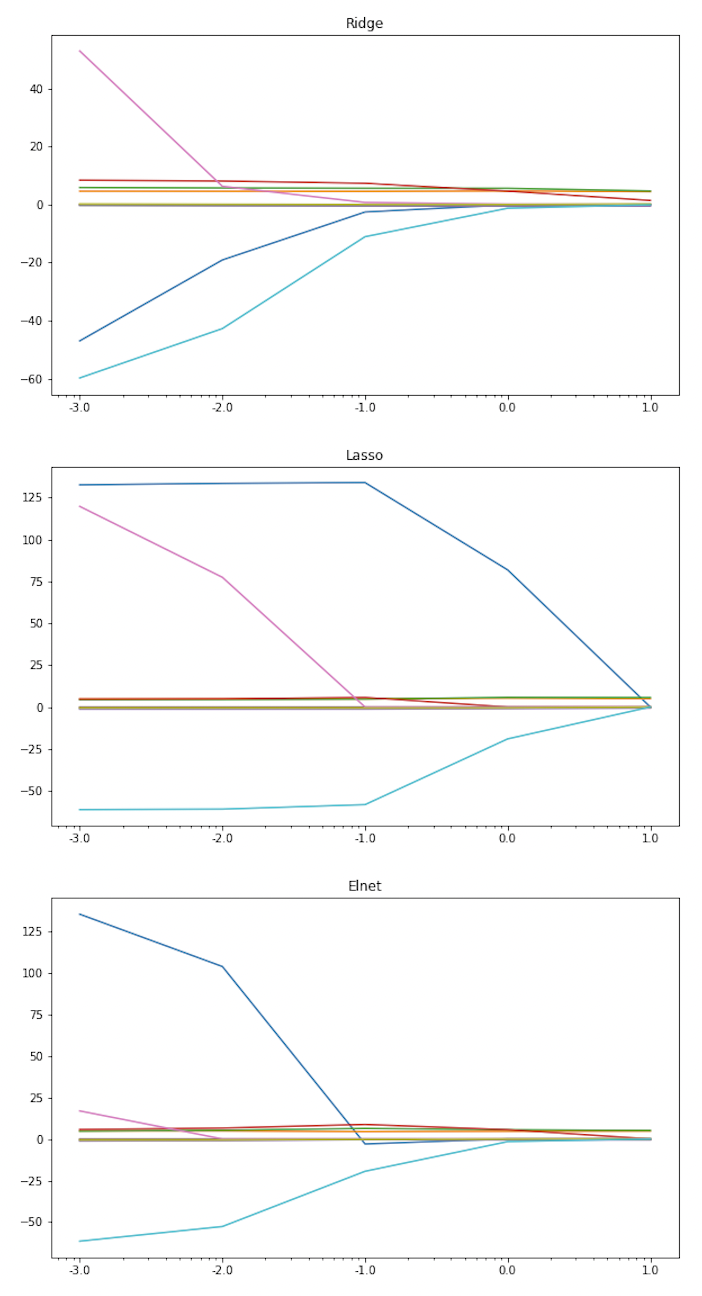
반면, 최적의 alpha 값을 찾는 것은 train data가 아닌 validation data가 기준이 되어야 하므로, validation data를 이용해 간단한 hyperparameter tuning을 해보면 다음과 같다.

# Tune alpha with validation
from sklearn.metrics import mean_squared_error
def tune_alpha(y, X, y_val, X_val, wt_list):
    alpha = np.logspace(-3,1,5) # 10^-3 to 10^1 by sqrt(10)
    data = []
    for wt in wt_list:
        data_wt = []
        for i, a in enumerate(alpha):
            model = sm.OLS(y, X).fit_regularized(method='elastic_net', alpha = a, L1_wt=wt)
            pred = model.predict(X_val)
            rmse = np.sqrt(mean_squared_error(y_val, pred)).round(3)
            data_wt.append(rmse)
        data.append(data_wt)
    df = pd.DataFrame(data, index=wt_list)
    df.columns = alpha
    return df

tune_alpha(y_train, X_train, y_val, X_val, wt_list=[1, 0.5, 0]) # lasso to ridge

결과는 다음과 같은데, 각 행은 L1_wt 즉 elastic-net의 형태를 의미하고 각 열은 hyperparameter인 규제 강도 alpha 값을 의미하며 각 셀의 데이터는 validation data에 대한 rmse 값을 의미한다.

	0.001	0.01	0.1	1	10
1.0	53.806	53.830	54.141	53.682	53.168
0.5	54.171	54.114	54.388	53.496	53.287
0.0	53.244	53.110	53.496	53.349	53.480

자세한 튜닝을 해보기 위해 이번에는 plot을 그려보고, alpha의 그리드를 더 잘게 탐색해보도록 하자. 우선 앞선 함수 tune_alpha()를 약간 수정해 wt_list=[1,0.5,0] 은 그대로 두고 alpha값들을 리스트로 받는 함수로 변경했다(코드는 생략, github full code 참고). 이후 아래와 같이 데이터프레임을 구하고 plot을 생성했다.

# Tune alpha plot
alpha_ls = np.power(10,(np.arange(-4, 1, 0.5))) # 10 grid of alpha
df = tune_alpha(y_train, X_train, y_val, X_val, alpha_ls=alpha_ls)

fig = plt.figure(figsize=(10,10))
plt.semilogx(df, label=['Lasso','Elastic-Net','Ridge'])
plt.legend(loc='upper right', title = 'Model')
plt.xticks(alpha_ls, labels=np.log10(alpha_ls))
plt.ylabel('RMSE')
plt.xlabel('alpha(10^x)')
plt.title('RMSE vs. alpha for 3 model')
plt.savefig('plots/rmse_vs_alpha.png', facecolor='white', transparent=False)

결과는 아래와 같은데, 이를 보면 Lasso의 경우 $\alpha=1.0$에서 전역 최소가 발생하고, Elastic-Net과 Ridge는 $\alpha=\sqrt{10}$에서 최소인 것 처럼 보이지만서도 Ridge의 경우는 $10^{-2}$에서 전역 최소가 된다. 세 모델을 모두 고려한다면, Ridge에서 $\alpha=0.01$인 경우가 가장 낮은 validation RMSE를 가지므로 이를 택하는 것이 좋아보인다.

스크린샷 2022-04-11 오후 7.19.09

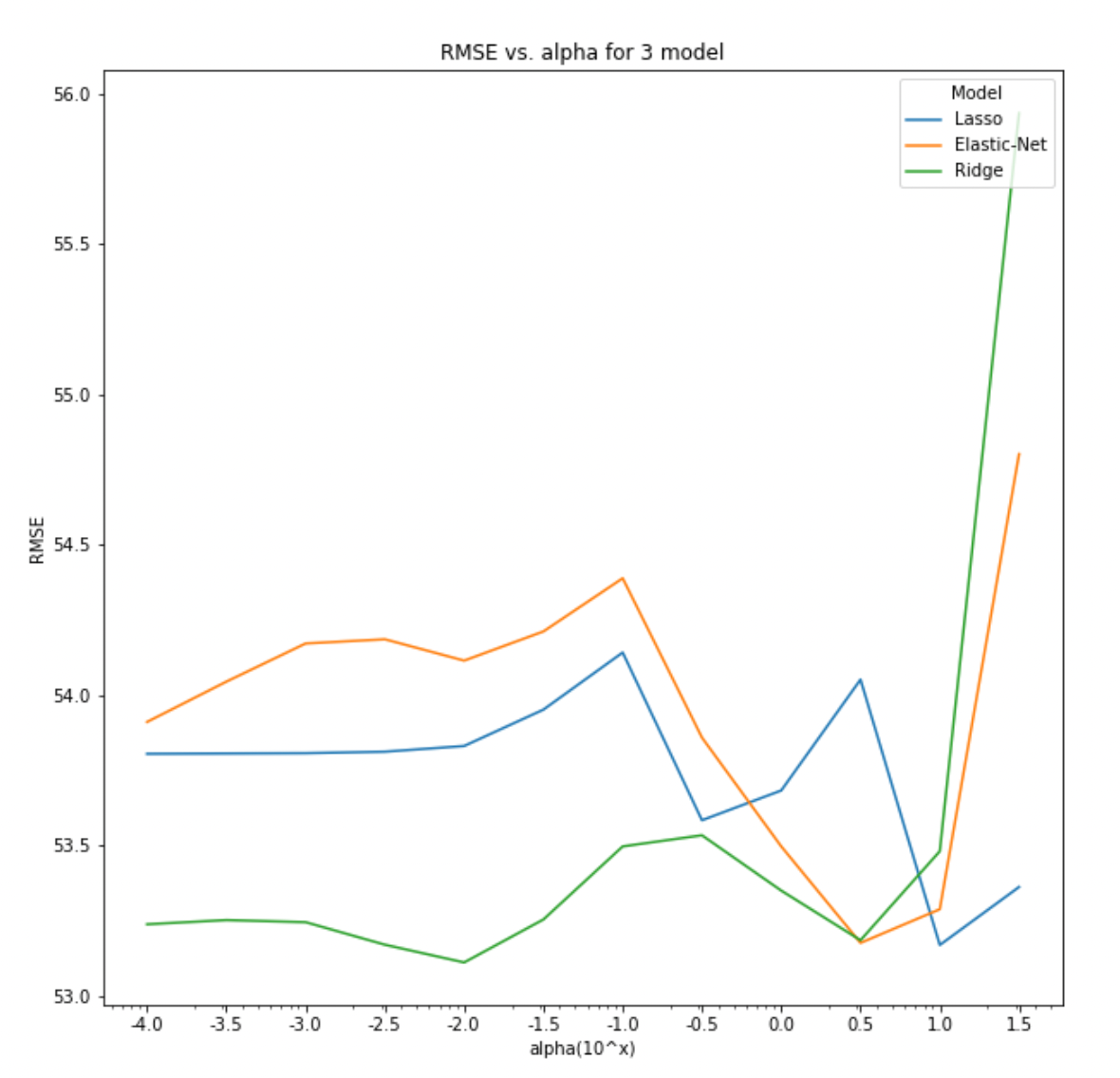
Least Angle Regression

LARS로 불리는 Least Angle Regression은 고차원 데이터에 대해 효과적인 방법인데, forward-stepwise regression(이전 포스트 참고)와 유사하게 변수들을 하나씩 추가하면서 모형을 생성해나간다(자세한 알고리즘은 링크 참고). 다만, high-dimensional data에서 특별히 계산적으로 유용한 것이므로(추후 고차원데이터 샘플을 구하면 연구해보도록 하겠다), 여기서는 작동 코드만 파악해보도록 하자. 안타깝게도, statsmodels 패키지는 LARS를 직접 수행할 수 있는 모듈을 제공하지 않으므로 대표적인 머신러닝 패키지 scikit-learn을 이용해보도록 하자. sklearn.linear_model의 Lars를 이용해 다음 코드와 같이 Lars 모델을 생성하고 validation data에 대한 RMSE를 계산할 수 있다.

# LARS
from sklearn import linear_model
reg = linear_model.Lars(n_nonzero_coefs=5, fit_intercept=True, normalize=False)
reg.fit(X_train, y_train)
pred_val = reg.predict(X_val)
rmse = np.sqrt(mean_squared_error(y_val, pred_val)).round(3)
print(rmse) # 53.242

LARS 알고리즘은 변수를 하나씩 fitting하며 중간에 0이 되는 회귀계수가 제거되는 방식인데, 여기서 n_nonzero_coefs=10은 0이 되는 변수들을 제거하고 남은 nonzero 변수들을 몇 개로 설정할 것인지 정하는 hyperparmeter의 일종이다. 또한 reg.coef_path_ attribute는 Lars 알고리즘이 어떻게 진행되는지, 즉 회귀계수가 각 단계마다 어떻게 변하는지 확인할 수 있게끔 해준다. 다음 코드

pd.DataFrame(reg.coef_path_, index = X_train.columns).round(3)

를 통해 각 변수(행)가 각 단계(열)마다 어떤 회귀계수를 갖는지 확인할 수 있다. 결과는 아래 표와 같은데, 가장 첫 단계에서 visibility가 반응변수와 가장 높은 상관관계를 가지게 되어 초기 변수로 선택되었고, 이를 기반으로 알고리즘이 진행되며 계수가 0이 아닌 변수가 hour, temp, humidity, visibility, pm10으로 5개가 도출된 것을 확인할 수 있다.

	1	2	3	4	5
const	0.000	0.000	0.000	0.000	0.000
hour	0.000	0.000	1.771	2.639	4.904
temp	0.000	0.000	0.000	0.000	5.799
windspeed	0.000	0.000	0.000	0.000	0.000
humidity	0.000	-0.579	-0.694	-0.834	-0.516
visibility	0.045	0.034	0.028	0.021	0.008
ozone	0.000	0.000	0.000	0.000	0.000
pm10	0.000	0.000	0.000	-0.095	-0.270
pm2_5	0.000	0.000	0.000	0.000	0.000
precip_1.0	0.000	0.000	0.000	0.000	0.000

🖥 Full code on Github : https://github.com/ddangchani/project_ddareungi

References

https://datascienceschool.net/03%20machine%20learning/06.05%20정규화%20선형회귀.html